A sphere of mass m and radius R rolls without sliding on a horizontal surface. It collides with a light spring of stiffness K with a kinetic energy E. If the surface (AB) under the spring is smooth, find the maximum compression of the spring.
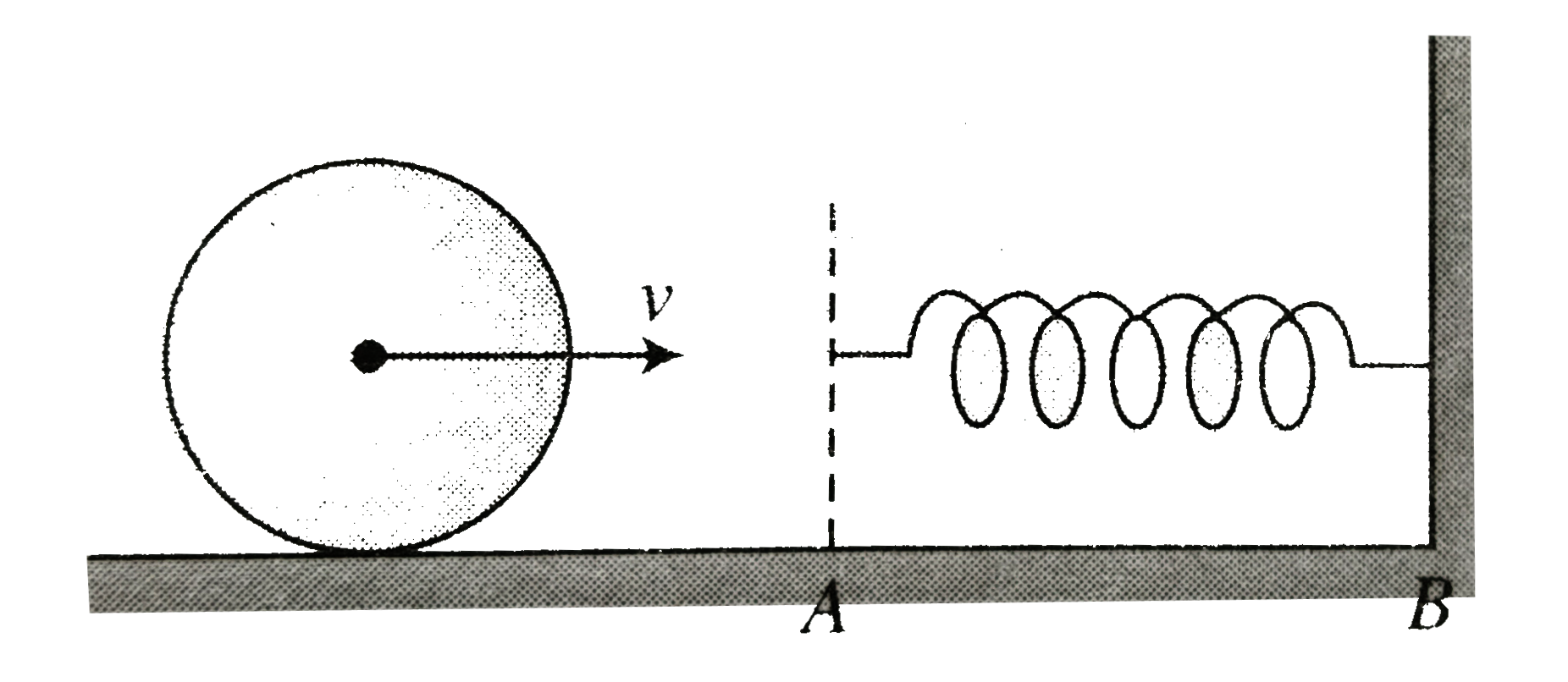
The total kinetic energy of the sphere =E=Etran+Erot
=12mv2+1225mR2v2R2=710mv2⇒v=√10E7m
Since the spring force F passes through the centre O of the sphere, it cause no torque about O. therefore, the angular momentum and hence angular velocity of the sphere remains constant. Since the surface AB is smooth no frictional loss take place. Therefore, conserve in the energy of the system (sphere spring) between the given (initial) position and the final position (maximum compression of the spring), we obtain
△KEsphere+△Espring=0
⇒△KEtran+△KErot+△PEspring=0
Since the initial angular velocity of the sphere remains constant due to the absence of friction.

△KErotation=0⇒△KEtrans+△PEspring=0
=(0−12mv2)+(12kx2−0)=0
where v=√10E7m and x= maximum compression of the spring
⇒12Kx2=12m(√10E7m2)⇒x2=10E7k
⇒x=√10E7k
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.213videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
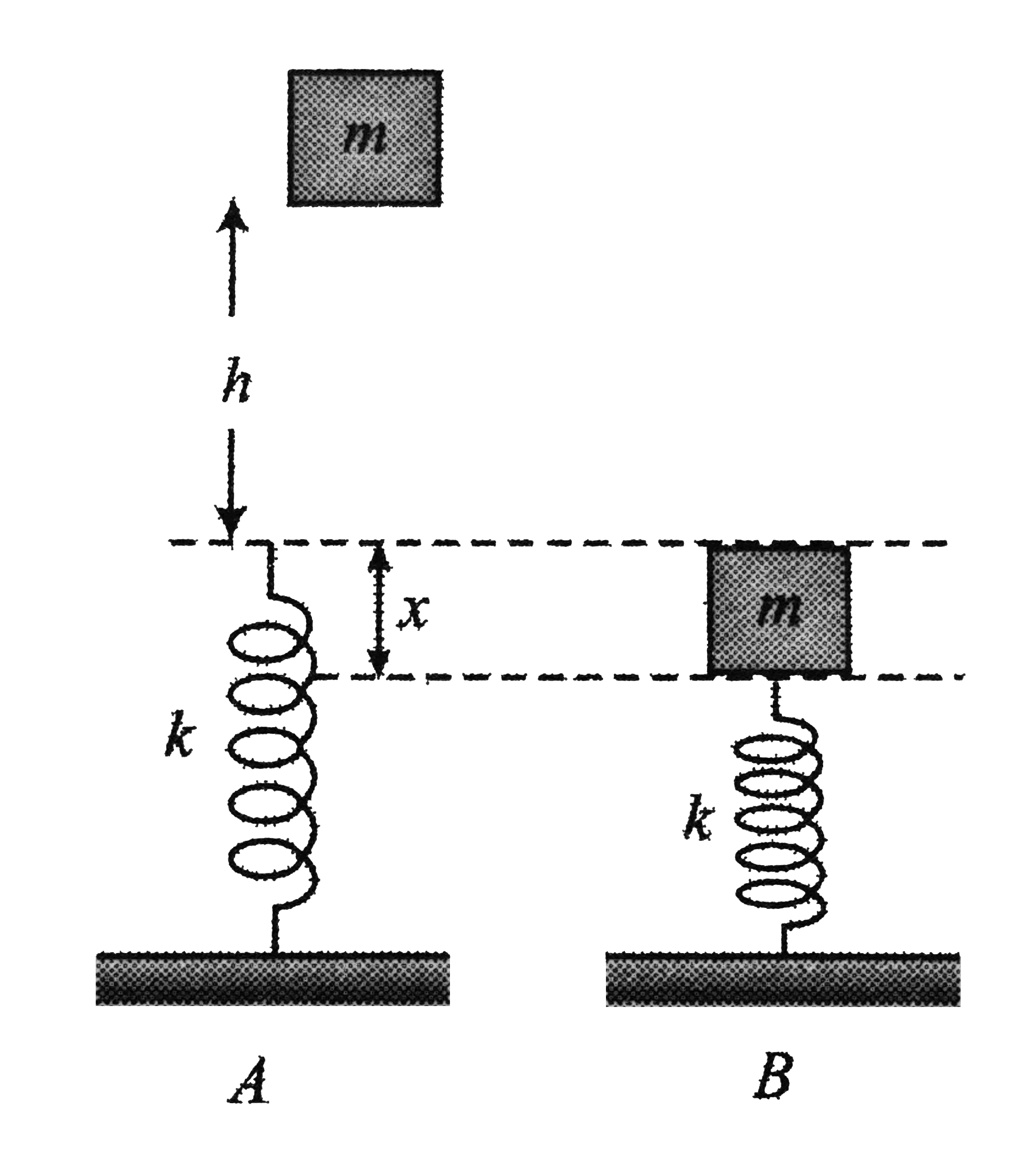
A block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
 View Solution
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct. - Question 2 - Select One
A loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
A1/2Mv2B3/2Mv2CMv2D1/2MR2ω2 - Question 3 - Select One
A sphere is rolling on a horizontal surface without slipping. The ratio of the rotational K.E. to the total kinetic energy of the sphere is
A25B27C57D37
A bullted of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial sped of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time forthe bullet - block system to come to rest.
View SolutionA small mass 'm' is sliding down on a smooth curved incline form a height 'h' and finally moves through a horizontal smooth surface. A light spring of force constant K is fixed with a vertical rigid stand on the horizontal surface, as shown in the figure. Find the value for the maximum compression in the spring if mass 'm' is released from rest from height 'h' and hits the spring in the horizontal surface.
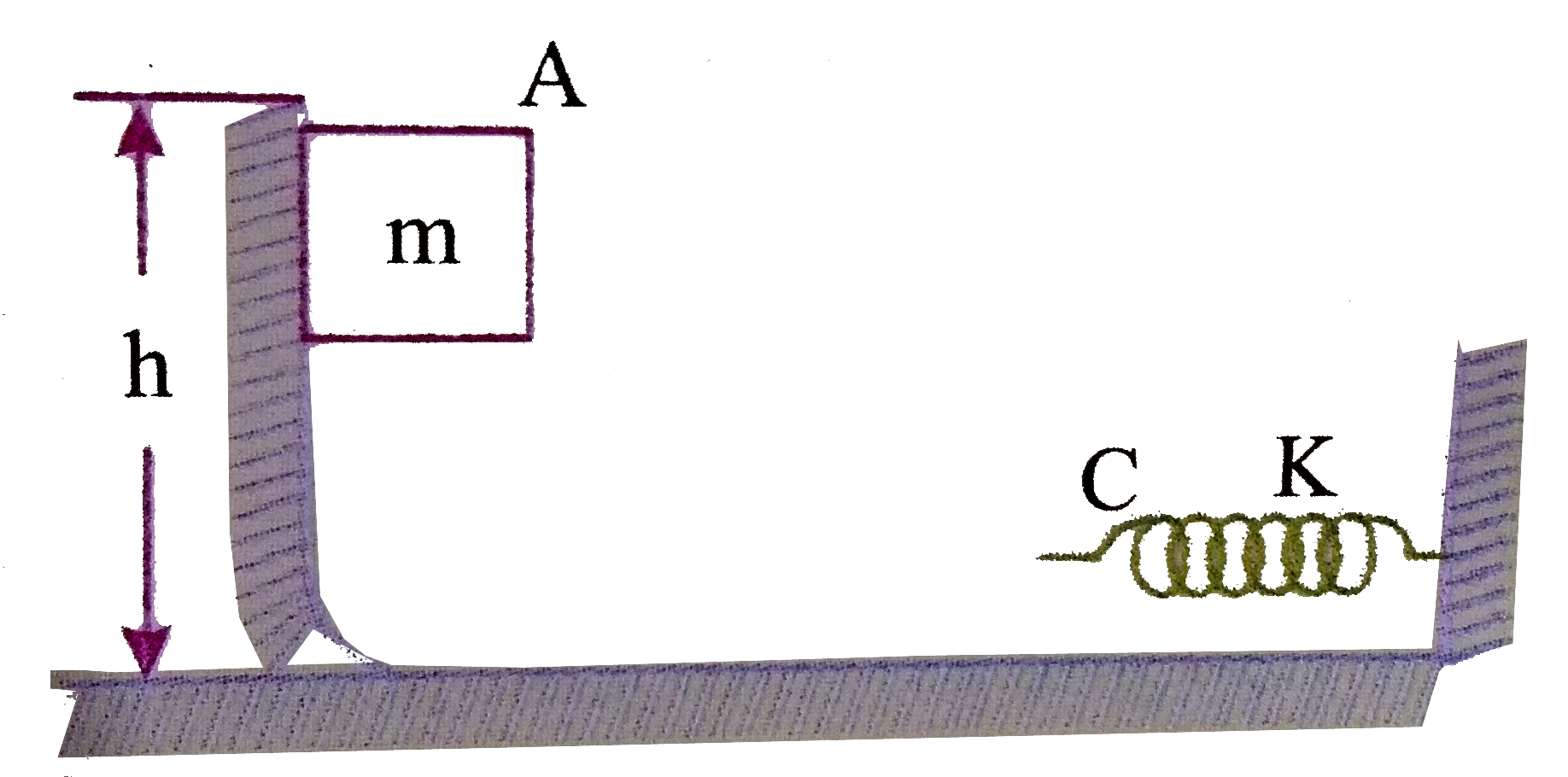 .View Solution
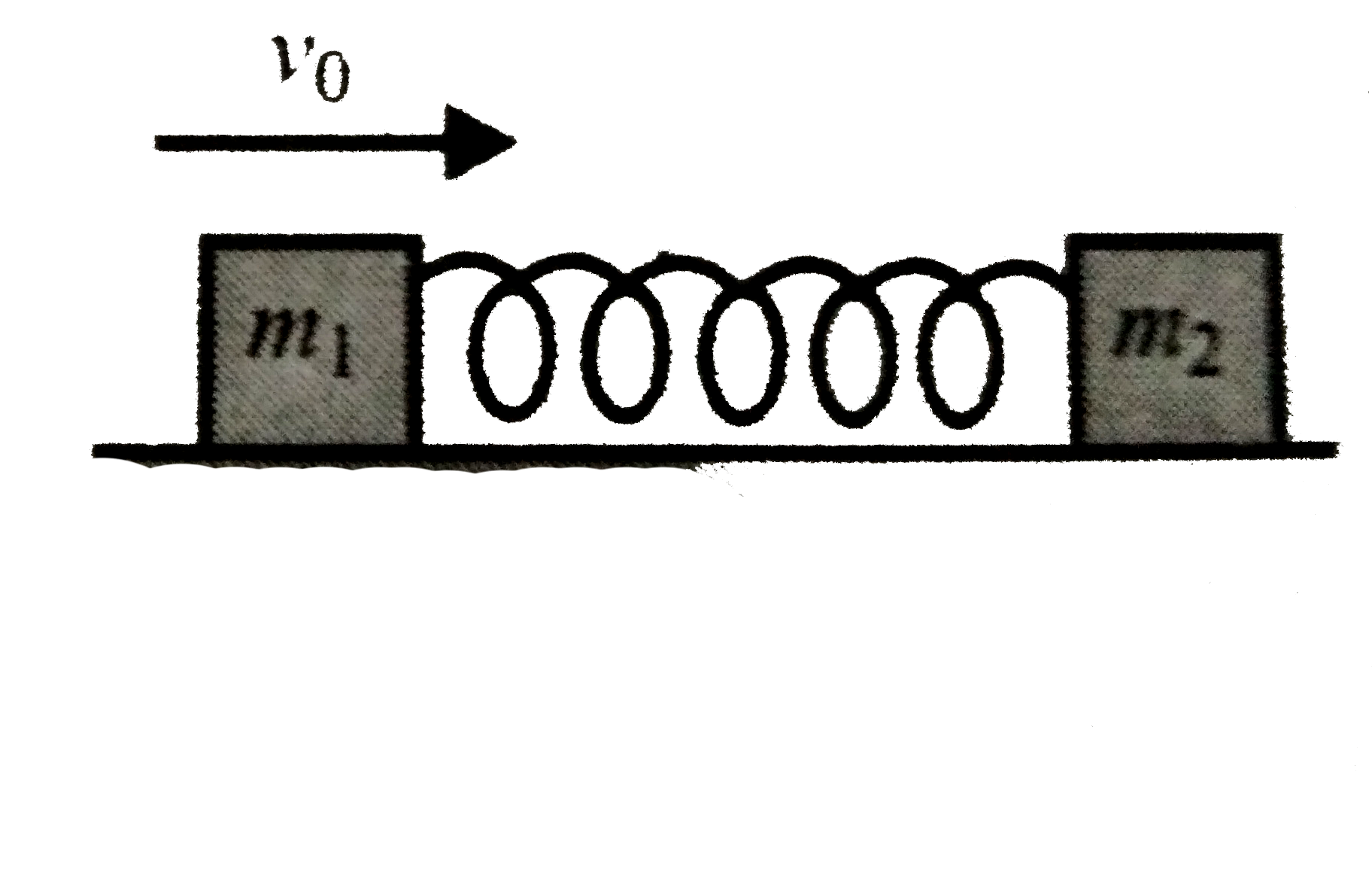
.View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
 View Solution
View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 View Solution
View SolutionA uniform solid sphere A of mass m is rolling without sliding on a a smooth horizontal surface. It collides elastically and head - on with another stationary hollow sphere B of the same mass and radius. Assuming friction to be absent everywhere, the ratio of the kinetic energy of B to that of A just after the collision is
 View Solution
View Solution

