A sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
Since →LP=→Lcm+→r×→ρcm=Icm→ω+→R×m→vcm
Since sphere is in pure rolling motion hence ω=v0/R
⇒ →L=(25MR2)v0R(−ˆk)+Mv0R(−ˆk)=75Mv0R(−ˆk)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - I
Explore 15 Videos
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
Explore 15 Videos
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:NUMERICALS BASED QUESTIONS
Explore 4 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Numerical Based Question Decimal Type
Explore 6 Videos
- SEMICONDUCTOR AND DEVICEBook:FIITJEEChapter:SEMICONDUCTOR AND DEVICEExercise:SOLVED PROBLEMS Objective: Level-I
Explore 20 Videos
Similar Questions
A solid sphere is rolling on a horizontal surface such that speed of the centre of sphere is u. Mase of the sphere is m and radius R. Magnitude of angular momentum about the point of contact is found to be 7nmvR/. Find the value of n
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View Solution
Knowledge Check
A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
A75gsinθB27gsinθC37gsinθD57gsinθA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.
A solid sphere of mass m and radius R is rolling without slipping on a rough horizontal surface with angular acceleration α. Centre of mass of sphere lies at a distance R√2 from the centre of sphere. Find the normal force applied by sphere on the surface at an instant when line joining centre of mass of sphere and centre of sphere makes an angle 45∘ with the vertical and angular velocity of sphere at this instant is ω.Amg+mR2(α−ω2)Bmg−mR2(α+ω2)Cmg−mR2(α−ω2)Dmg+mR2(α+ω2)
A uniform sphere of mass m and radius R starts rolling without slipping down an inclined plane at an angle α to the horizontal. Find the time dependence of the angular momentum of the sphere relative to the point of contact at the initial moment. How will the obtained result change in the case of a perfectly smooth inclined plane?
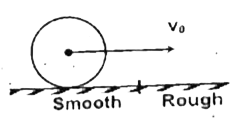
View SolutionA sphere moving with a speed v0 on a smooth surface suddenly enters on a rough horizontal surface as shown. The angular momentum of the sphere about any point on the surface is conserved.
View SolutionA symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
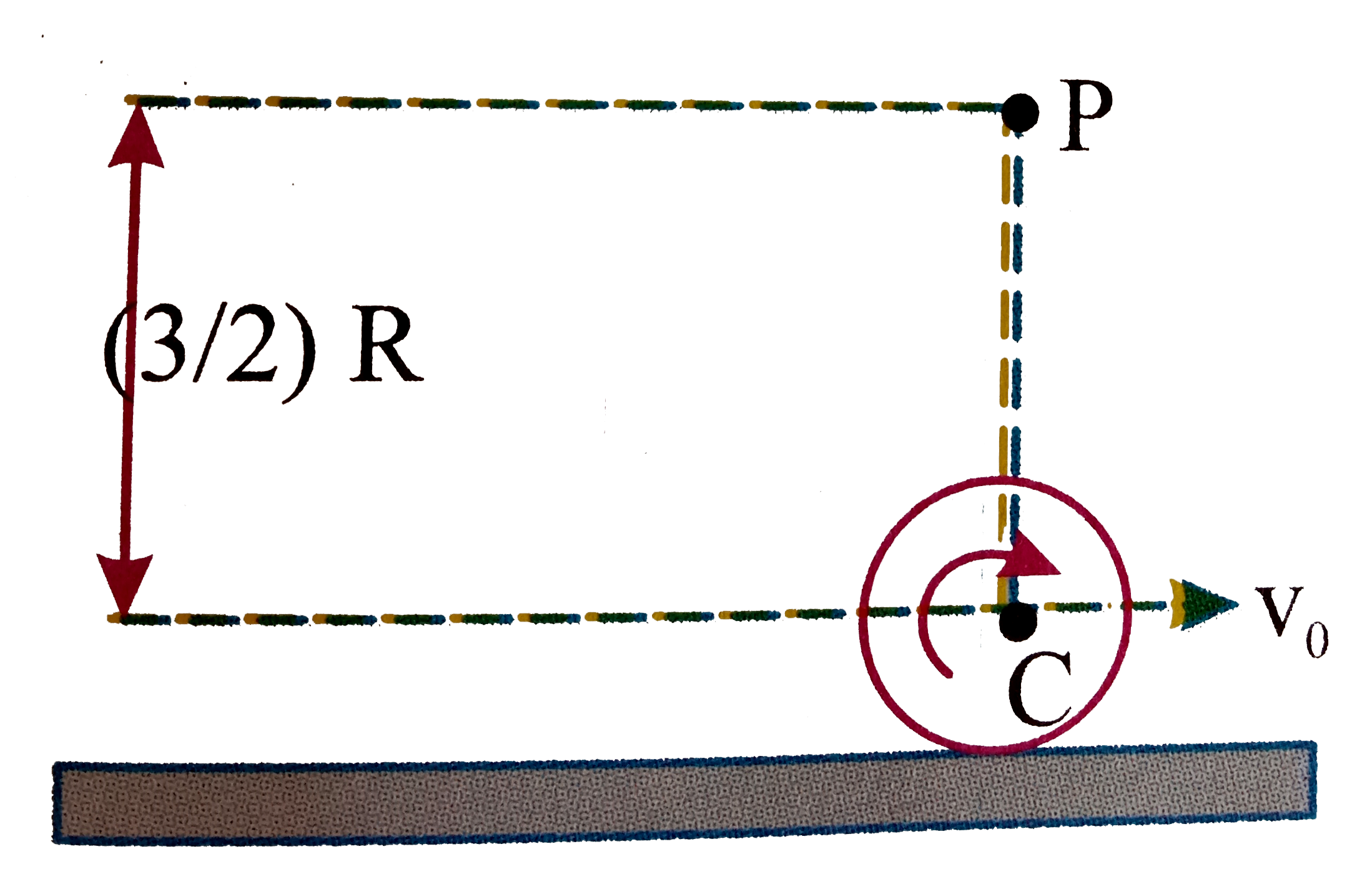
View SolutionIf a solid sphere of mass 500 gram rolls without slipping with a velocity of 20 cm/s, then the rolling kinetic energy of the sphere will be
View Solution
