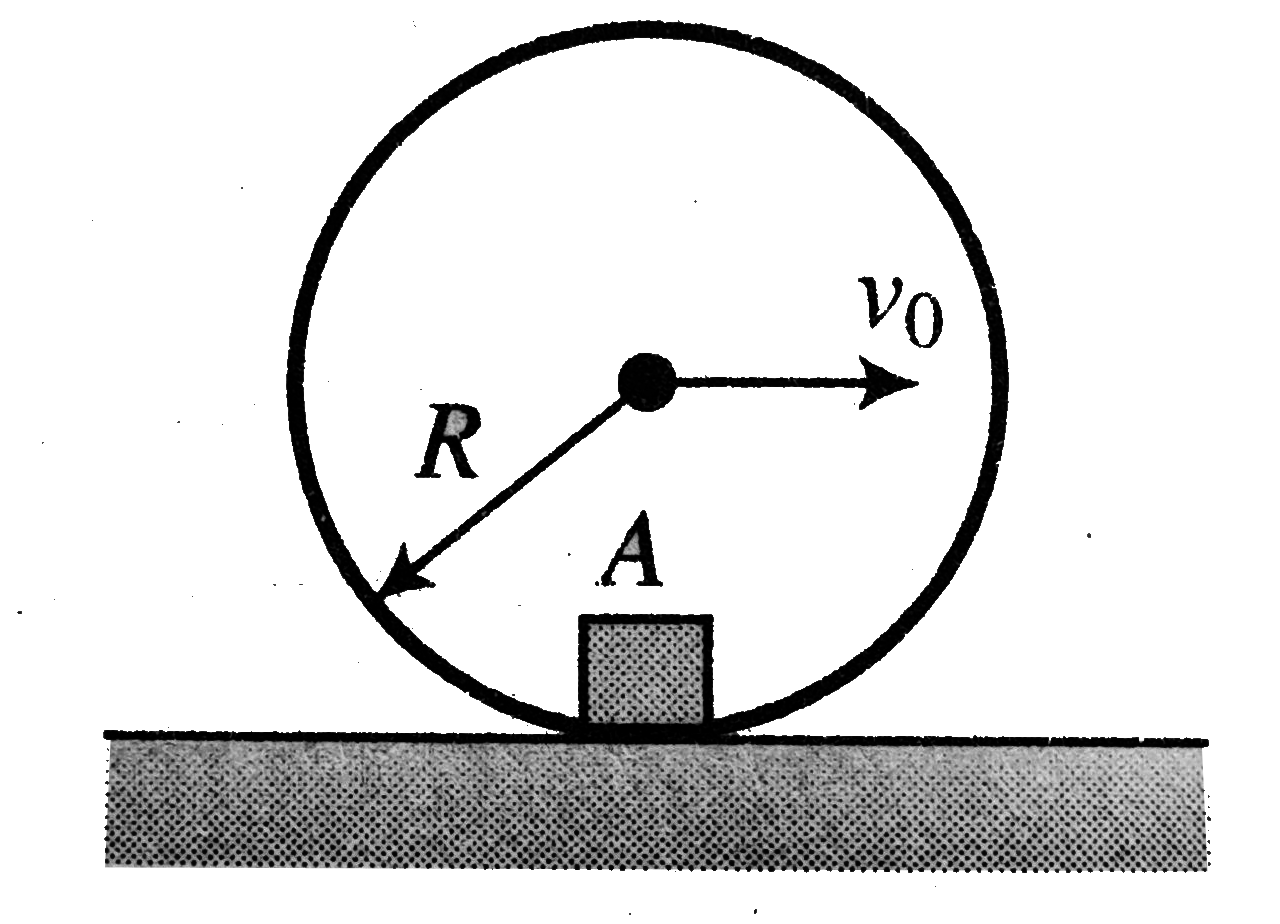
A small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane, at the moments when the body A gets into the lower position, the centre of the hoop moves with velocity v0(figure). At what values of v0 will the hoop move without bouncing?

The correct Answer is:√8gR
Step by step video, text & image solution for A small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane, at the moments when the body A gets into the lower position, the centre of the hoop moves with velocity v_0(figure). At what values of v_0 will the hoop move without bouncing? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - I
41 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - II
16 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - I
15 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
A small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane, at the moments when the body A gets into the lower position, the centre of the hoop moves with velocity v0. At what values of v0 will the hoop move without bouncing?
View SolutionA uniform sphere of mass m and radius r rolls without sliding over a horizontal plane, rotating ahout a horizontal axle OA. In the process, the centre of the sphere moves with a veocity v along a circle of radius R. Find the kinetic energy of the sphere.
View Solution
Knowledge Check
A rigid body of radius R and radius of gyration k rolls without slipping along a horizontal plane. Then, the ratio of its rotational energy to total energy is
Ak2R2Bk2k2+R2CR2k2DR2k2+R2
A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration atAA is vertically upwardsBB may be vertically downwardsCC cannot be horizontalDA point on the rim may be horizontal leftwards.A hollow sphere of radius R and mass m fully filled with water of mass m. It is rolled down a horizontal plane such that its centre of mass moves with a velocity v. If it purely rolls.
AKinetic energy of the sphere is 56mv2BKinetic energy of the sphere is 45mv2CAngular momentum of the sphere about a fixed point on ground is 82mvRDAngular momentum of the sphere about a fixed point ground is 145mvR.
A uniform solid cylinder of radius 'R' has a circular cut of radius R2 from the edge, Its mass is M. It is rolling wihtout slipping on a rough horizontal floor. When the cut part is at lowest position, centre of the disc is moving with horizontal velocity v. Choose the alternative:
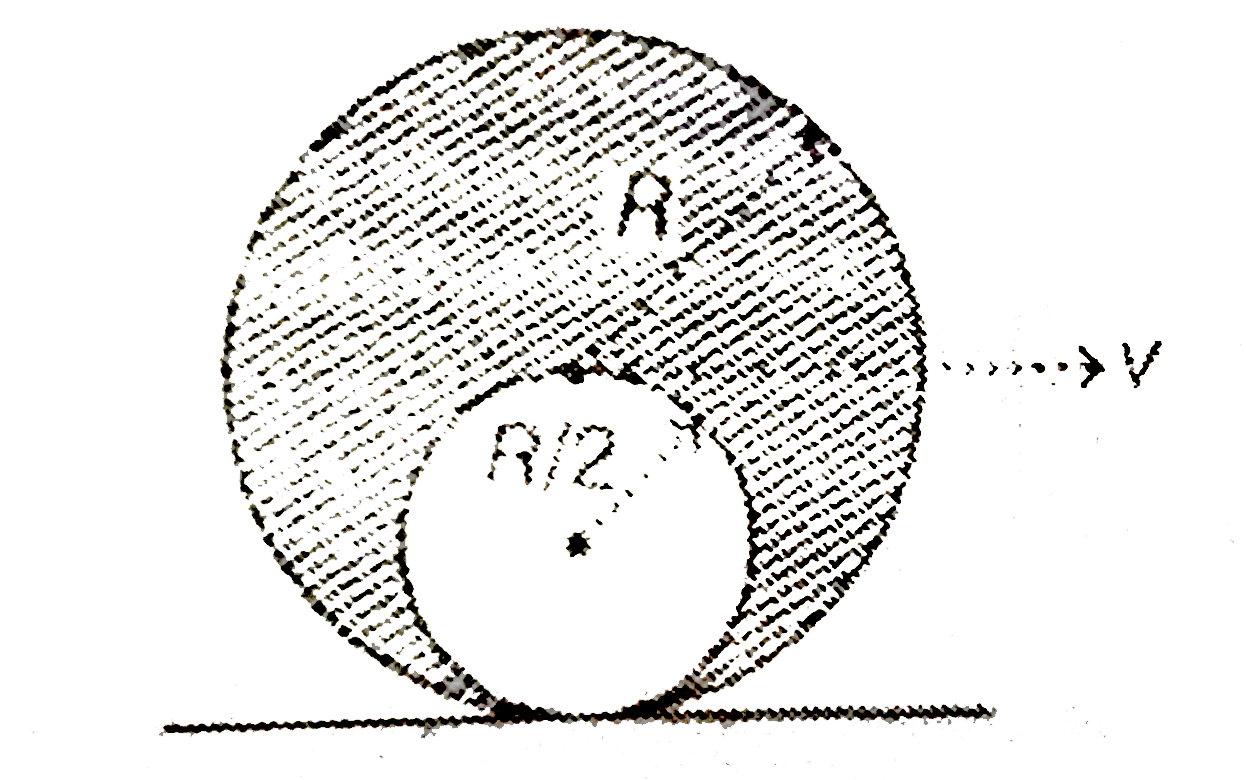
View SolutionA hoop and a solid cylinder have the same mass and radius. They both roll,without slipping, on horizontal surface. If their kinetic energies are equal -
View SolutionA round unifrom body of radius R, mass M and moment of inertia I rolls down (without slipping) an inclined plane making an angle theta with the horizontal. Then its acceleration
View SolutionA round uniform body of radius R, mass M and moment of inertia 'I' rolls down (without slipping) and inclined plane making an angle θ with the horizontal. Then its acceleration is.
View SolutionA hoop of radius r and mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
View Solution
