The free end of a thread wound on a bobbin is passed round a nail A hammered into the wall. The thread is pulled at a constant velocity 'v' . Assuming pure rolling of bobin, find the velocity v0 of the centre of the bobbin at the instant when the thread forms an angle α with the vertical: (R and r are outer and inner radii off the babbin)

The correct Answer is:RvRsinα−r
Step by step video, text & image solution for The free end of a thread wound on a bobbin is passed round a nail A hammered into the wall. The thread is pulled at a constant velocity 'v' . Assuming pure rolling of bobin, find the velocity v_(0) of the centre of the bobbin at the instant when the thread forms an angle alpha with the vertical: (R and r are outer and inner radii off the babbin) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - I41videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - II16videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - I15videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type6videos
PHYSICS PART2
- BOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I20videos
SEMICONDUCTOR AND DEVICE
Similar Questions
Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.
 View Solution
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0 and forms an angle α with the horizontal.
View Solution
Knowledge Check
- Question 1 - Select One or More
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘
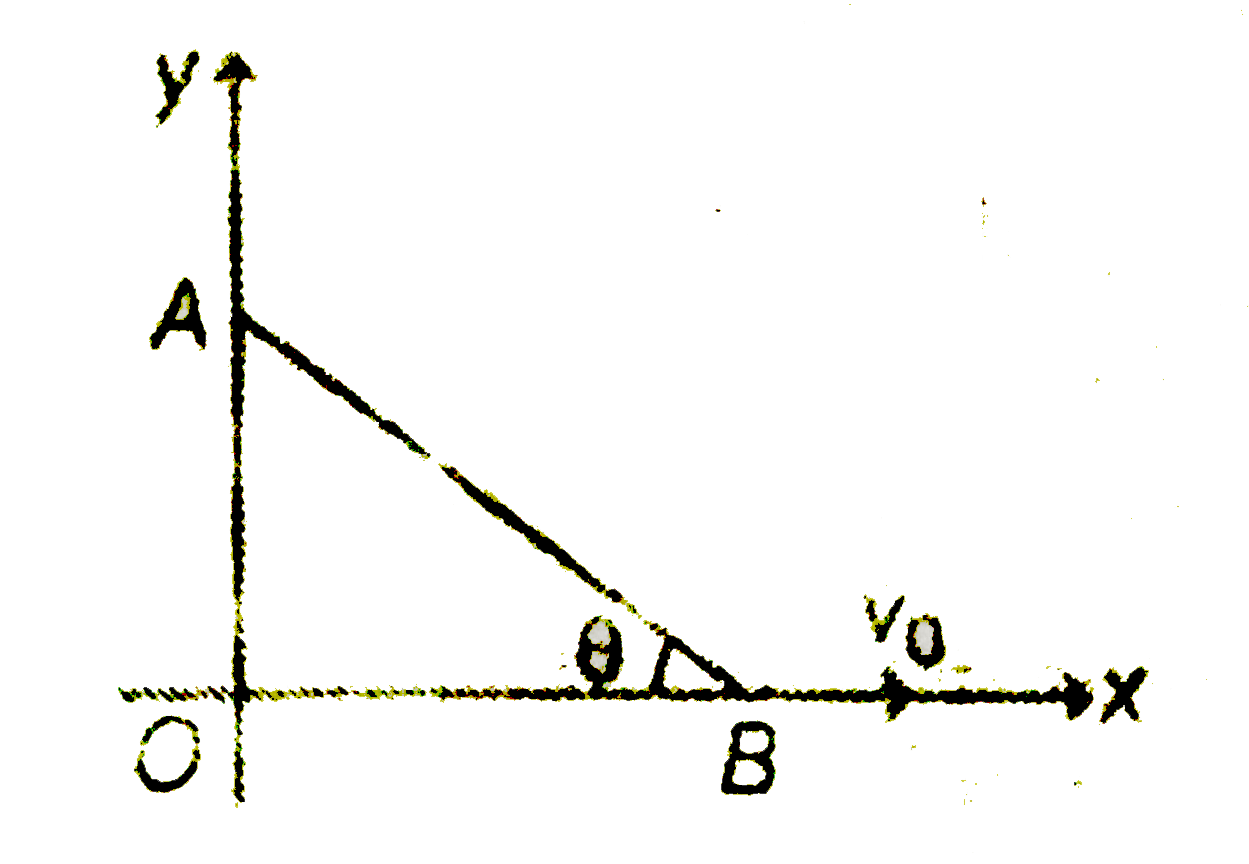 Avelocity of end A is 43v0 downwardsBangular velocity of rod is 53v0lCangular velocity of rod is constantDvelocity of end A is constant
Avelocity of end A is 43v0 downwardsBangular velocity of rod is 53v0lCangular velocity of rod is constantDvelocity of end A is constant - Question 2 - Select One
End A of a rod AB is being pulled on the floor with a constant velocity v0 as shown. Taking the length of the rod as l, at an instant when the rod makes an angle 37∘ with the horizontal, calculate

the velocity of the CM of the rodA57v0 at tan−143 below horizontalB57v0 at tan−134 below horizontalC56v0 at tan−134 below horizontalD56v0 at tan−143 below horizontal - Question 3 - Select One
A uniform circular loop of radius a and resistance R is pulled at a constant velocity v out of a region of a uniform plane of the loop and the velocity are both perpendicular to B. Then the electrical power in the circular loop at the instant when the arc (of the circular loop) outside the region of magnetic field subtends an angle π3 at the centre of the loop is
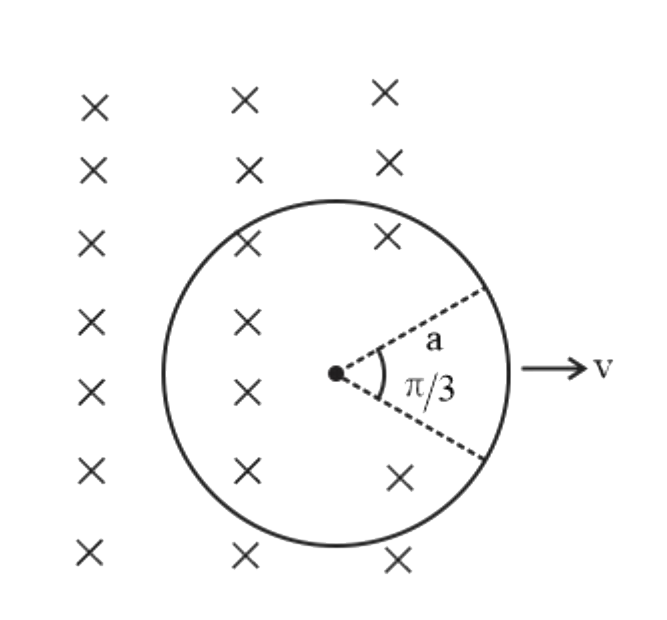 AB2a2v2RB2B2a2v2RCB2a2v22RDnone of these
AB2a2v2RB2B2a2v2RCB2a2v22RDnone of these
A light thread is tightly wrapped around a fixed disc of radius R. A particle of mass m is tied to the end P of the thread and the vertically hanging part of the string has length πR. The particle is imparted a horizontal velocity V=√4πgR3. The string wraps around the disc as the particle moves up. At the instant the velocity of the particle makes an angle of θ=60∘ with horizontal, calculate.
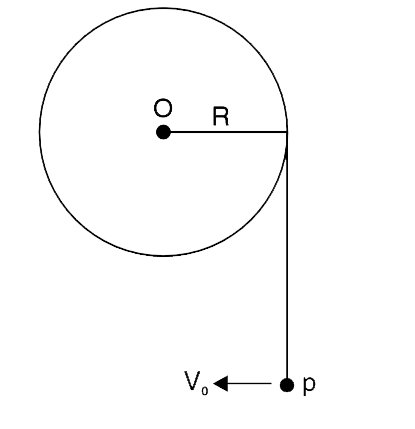
(a) Speed of the particle
(b) Tension in the stringView SolutionA round cone with half-angle α=30∘ and the radius of the base R=5.0cm rolls uniformly and without slipping over a horizontal plane as shown in fiugre. The cone apex is hinged at the point O which is one the same level with the point C, the cone base centre. The velocity of point C is v=10.0cm/s. Find the moduli of
(a) the vector of the angular velocity of the cone and the angle it forms with the vertical,
(b) the vector of the angular acceleration of the cone.
 View Solution
View SolutionA ring of mass M and radius R lies flat on a horizontal table. A light thread is wound around it and its free end is pulled with a constant velocity v.
(a) Two small segment A and B (see fig.) in the ring are rough and have a coefficient of friction μ with the table. Rest of the ring is smooth. Find the speed with which the ring moves.
(b) Find the speed of the ring if coefficient of friction is μ everywhere, for all points on the ring.
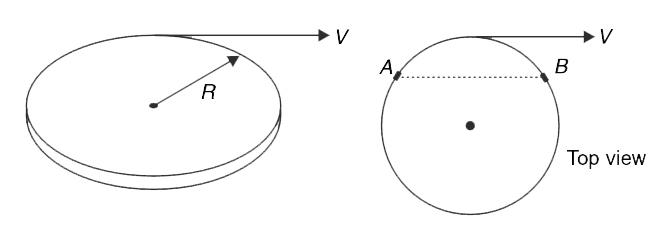 View Solution
View SolutionA projectile, thrown with velocity v0 at an angle α to the horizontal, has a range R. it will strike a vertical wall at a distance R/2 from the point of projection with a speed of
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
View Solution

