Least Integer Function:
We know that any real number x can be expressed as following x= [x] + {x}, where [x] is an integer and 0≤{x}<1. We define [x] as the greatest integer less than or equal to x or integral part of x and (x} as the fractional part of x:
Suppose for any real number x we write x = [x]+{x}, where [x] is integer and 0≤{x}<1. We define (x) as the least integer greater than or equal to x. For example:
(2.36) = 3
(-13.11) =-13
(4)=4
Clearly, If x≠I, then (x)=x -{x}+1
if x ∈ I, then (x) = [x] +1.
We can also define that ξn(n,n+1]⇒(x)=n+1, where n∈I.
The domain of definition of the function f(x)=1√x−{x} is

A

I

B

R~I

C

(0,∞)

D

ϕ

Text Solution
Verified by Experts

The correct Answer is:D

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSFUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Least Integer Function:
    We know that any real number x can be expressed as following x= [x] + {x}, where (x) is an integer and 0≤{x}<1. We define [x] as the greatest integer less than or equal to x or integral part of x and (x} as the fractional part of x:
    Suppose for any real number x we write x = (x) - 0, whore (x) Is integer and 0≤(x)<1. We define (x) as the least integer greater than or equal to x. For example:
    (2.36) = 3
    (-13.11) =-13
    (4)=4
    Clearly, If ξnl, then (x)-{x]
    if x ∈ l, then (x) = [x] +1.
    We can also define that ξn(n,n+1]⇒(x)=n+1, where n∈I.
    The range of the function f(x)=1√(x)−[x] is

    Aϕ
    B{1}
    C{1√n,n∈N}
    D(1,∞)

  • Let [x] be the greatest integer less than or equal to x, for a real number x. Then the following sum
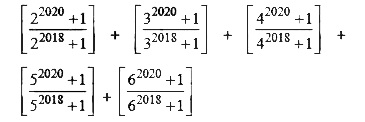
    ocr_image
    is-

    A80
    B85
    C90
    D95

  • Let [x] be the greatest integer less than or equal to x, for a real number x. Then the equation [x2]=x+1 has

    Atwo solutions
    Bone solution
    Cno solution
    Dmore than two solutions