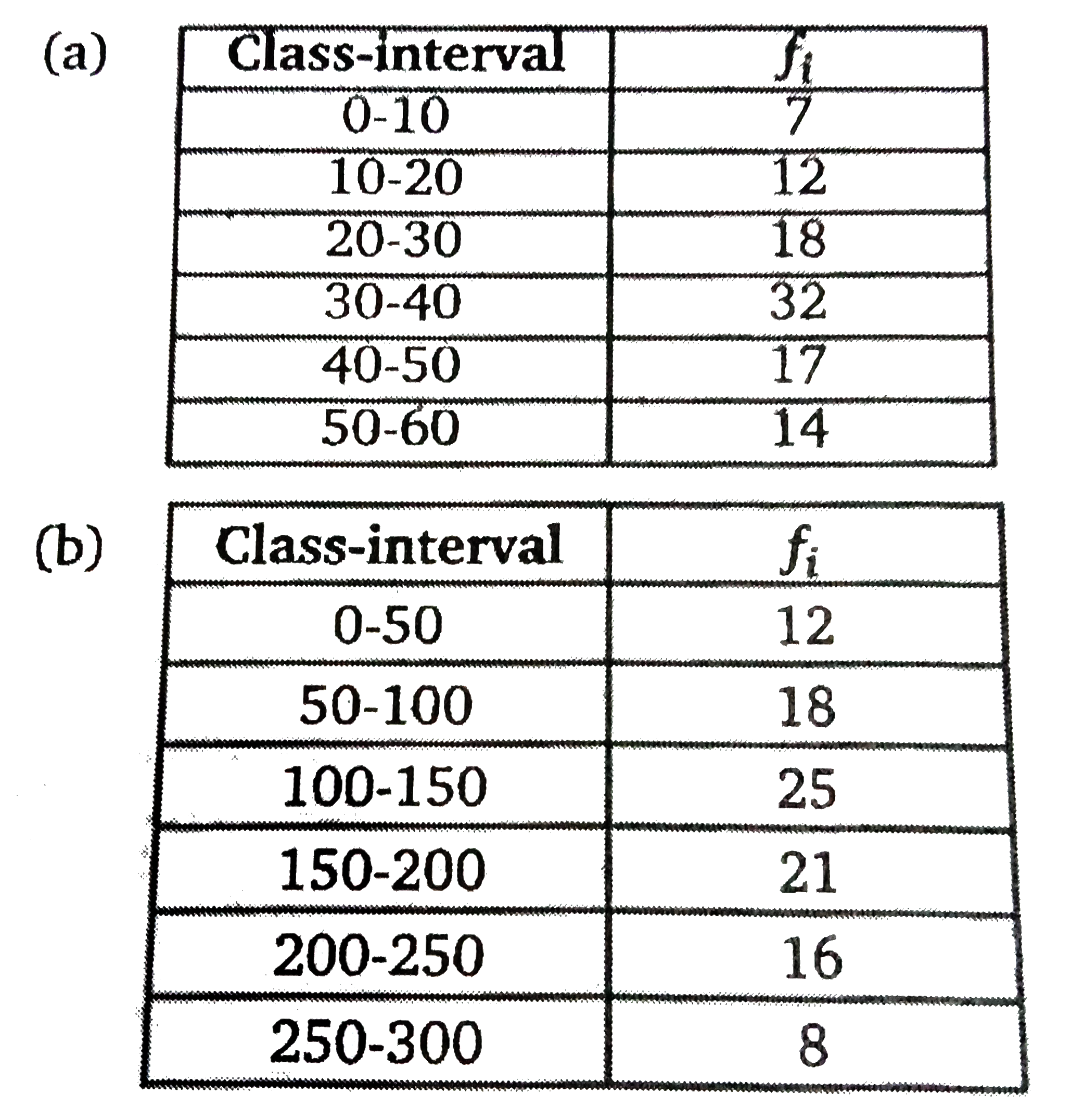
Find the mean deviation from the mean of the A.P., a,a+d, a+2d, .........,a+2nd.
To find the mean deviation from the mean of the arithmetic progression (A.P.) given by the terms a,a+d,a+2d,…,a+2nd, we will follow these steps:
Step 1: Identify the number of terms in the A.P.
The first term is a and the last term is a+2nd. The general term of the A.P. can be expressed as:
Tn=a+(n−1)d
To find the total number of terms, we set n−1=2n (since the last term is a+2nd). Solving for n:
n−1=2n⟹n=2n+1⟹n=2n+1⟹n=2n+1⟹n=2n+1⟹n=2n+1
Thus, the total number of terms is 2n+1.
Step 2: Calculate the mean of the A.P.
The mean ¯x of the A.P. is given by the formula:
¯x=Sum of all termsNumber of terms
The sum of the terms in the A.P. is:
S=a+(a+d)+(a+2d)+…+(a+2nd)
This can be simplified as:
S=(2n+1)a+d(0+1+2+…+2n)
Using the formula for the sum of the first m natural numbers m(m+1)2:
0+1+2+…+2n=2n(2n+1)2=n(2n+1)
Thus, the sum becomes:
S=(2n+1)a+d(n(2n+1))=(2n+1)(a+nd)
Now, substituting back into the mean formula:
¯x=(2n+1)(a+nd)2n+1=a+nd
Step 3: Calculate the mean deviation from the mean.
The mean deviation MD is calculated as:
MD=∑|xi−¯x|N
where N is the total number of terms, which is 2n+1.
The deviations from the mean are:
- For x0=a: |a−(a+nd)|=|−nd|=nd
- For x1=a+d: |(a+d)−(a+nd)|=|d−nd|=|(1−n)d|
- For x2=a+2d: |(a+2d)−(a+nd)|=|2d−nd|=|(2−n)d|
- Continuing this way until x2n=a+2nd: |(a+2nd)−(a+nd)|=|2nd−nd|=|nd|
The deviations can be summarized as:
nd,(1−n)d,(2−n)d,…,(n−1)d,0,(1−n)d,(2−n)d,…,nd
Step 4: Calculate the total deviation.
The total deviation is:
∑|xi−¯x|=nd+(1−n)d+(2−n)d+…+0+…+(n−1)d+(1−n)d+…+nd
This can be simplified by recognizing symmetry and the cancellation of terms.
Step 5: Final calculation of mean deviation.
The mean deviation simplifies to:
MD=2d⋅n(n+1)22n+1=nd(n+1)2n+1
Final Answer:
Thus, the mean deviation from the mean of the A.P. is:
Mean Deviation=nd(n+1)2n+1
The first term is a and the last term is a+2nd. The general term of the A.P. can be expressed as:
Tn=a+(n−1)d
To find the total number of terms, we set n−1=2n (since the last term is a+2nd). Solving for n:
n−1=2n⟹n=2n+1⟹n=2n+1⟹n=2n+1⟹n=2n+1⟹n=2n+1
Thus, the total number of terms is 2n+1.
The mean ¯x of the A.P. is given by the formula:
¯x=Sum of all termsNumber of terms
The sum of the terms in the A.P. is:
S=a+(a+d)+(a+2d)+…+(a+2nd)
This can be simplified as:
S=(2n+1)a+d(0+1+2+…+2n)
Using the formula for the sum of the first m natural numbers m(m+1)2:
0+1+2+…+2n=2n(2n+1)2=n(2n+1)
Thus, the sum becomes:
S=(2n+1)a+d(n(2n+1))=(2n+1)(a+nd)
Now, substituting back into the mean formula:
¯x=(2n+1)(a+nd)2n+1=a+nd
The mean deviation MD is calculated as:
MD=∑|xi−¯x|N
where N is the total number of terms, which is 2n+1.
- For x0=a: |a−(a+nd)|=|−nd|=nd
- For x1=a+d: |(a+d)−(a+nd)|=|d−nd|=|(1−n)d|
- For x2=a+2d: |(a+2d)−(a+nd)|=|2d−nd|=|(2−n)d|
- Continuing this way until x2n=a+2nd: |(a+2nd)−(a+nd)|=|2nd−nd|=|nd|
nd,(1−n)d,(2−n)d,…,(n−1)d,0,(1−n)d,(2−n)d,…,nd
The total deviation is:
∑|xi−¯x|=nd+(1−n)d+(2−n)d+…+0+…+(n−1)d+(1−n)d+…+nd
This can be simplified by recognizing symmetry and the cancellation of terms.
The mean deviation simplifies to:
MD=2d⋅n(n+1)22n+1=nd(n+1)2n+1
Thus, the mean deviation from the mean of the A.P. is:
Mean Deviation=nd(n+1)2n+1
Topper's Solved these Questions
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Solved Problems(Subjective)
9 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Solved Problems(Objective)
24 Videos
- SET, RELATION & FUNCTIONBOOK - FIITJEECHAPTER - SET, RELATION & FUNCTIONEXERCISE - Exercise 3
8 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - NUMERICAL BASED
4 Videos
Similar Questions
Knowledge Check
The mean deviations from the mean of AP a,a,d,a+2d,....,a+2nd is
An(n+1)d(2n+1)2Bn(n+1)d2n+1C2n(n+1)dnDn(n−1)d2n+1Find the mean deviation from the median of the following data
 A7.08B7C7.1D7.05
A7.08B7C7.1D7.05The mean deviation from the mean for the following data is
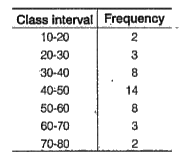 A5B10C15D20
A5B10C15D20
Find the mean deviation about the mean of the distributon .

View SolutionFind the mean deviation about the mean for the following data.

View SolutionFind the mean deviation about the mean for the following data :

View SolutionFind the mean deviation about the mean for the following data :

View SolutionThe mean deviation from the mean for the following data is
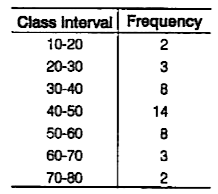
View Solution