A→A,ΔH=+Ve, Graph between log10Aand1T is straight line of slpe 14.606 find ΔH in cel
The correct Answer is:1
To solve the problem step by step, we will follow the reasoning provided in the video transcript and derive the value of ΔH in calories.
Step 1: Understand the relationship between ΔG, ΔH, and ΔS
We start with the thermodynamic relationship:
ΔG=ΔH−TΔS
And also, we know that:
ΔG=−2.303RTlogK
Where K is the equilibrium constant.
Step 2: Set the equations equal
By equating the two expressions for ΔG, we have:
−2.303RTlogK=ΔH−TΔS
Step 3: Rearrange the equation
Rearranging gives:
ΔH=TΔS−2.303RTlogK
Dividing through by T:
ΔHT=ΔS−2.303RlogK
Step 4: Identify the slope of the graph
From the problem, we know that the graph of logK versus 1T is a straight line. The slope m of this line can be expressed as:
m=−ΔH2.303R
Step 5: Substitute the given slope
We are given that the slope m=14.606. Thus, we can write:
−ΔH2.303R=14.606
Step 6: Solve for ΔH
Rearranging gives:
ΔH=−2.303R⋅14.606
Step 7: Substitute the value of R
The value of the gas constant R in calories is approximately 2cal/mol⋅K. Substituting this value in:
ΔH=−2.303⋅2⋅14.606
Step 8: Calculate ΔH
Calculating the numerical value:
ΔH=−2.303⋅24.606
ΔH≈−1.000cal/mol
Since ΔH is given as positive in the problem, we take the absolute value:
ΔH≈1.000cal/mol
Final Answer
Thus, the value of ΔH in calories is:
ΔH≈1cal/mol
We start with the thermodynamic relationship:
ΔG=ΔH−TΔS
And also, we know that:
ΔG=−2.303RTlogK
Where K is the equilibrium constant.
By equating the two expressions for ΔG, we have:
−2.303RTlogK=ΔH−TΔS
Rearranging gives:
ΔH=TΔS−2.303RTlogK
Dividing through by T:
ΔHT=ΔS−2.303RlogK
From the problem, we know that the graph of logK versus 1T is a straight line. The slope m of this line can be expressed as:
m=−ΔH2.303R
We are given that the slope m=14.606. Thus, we can write:
−ΔH2.303R=14.606
Rearranging gives:
ΔH=−2.303R⋅14.606
The value of the gas constant R in calories is approximately 2cal/mol⋅K. Substituting this value in:
ΔH=−2.303⋅2⋅14.606
Calculating the numerical value:
ΔH=−2.303⋅24.606
ΔH≈−1.000cal/mol
ΔH≈1.000cal/mol
Thus, the value of ΔH in calories is:
ΔH≈1cal/mol
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - EXERCISE14videos
CHEMICAL EQUILIBRIUM
- BOOK - FIITJEECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ( SHORT ANSWER TYPE QUESTIONS ) )7videos
CHEMICAL EQUILIBRIUM
- BOOK - FIITJEECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - REASONING TYPE QUESTION1videos
CHEMICAL EQUILIBRIUM
- BOOK - FIITJEECHAPTER - CHEMICAL ENERGETICS EXERCISE - NUMERICAL BASED QUESTIONS2videos
CHEMICAL ENERGETICS
- BOOK - FIITJEECHAPTER - CHEMICAL KINETICS AND RADIOACTIVITYEXERCISE - Exercise9videos
CHEMICAL KINETICS AND RADIOACTIVITY
Similar Questions
The graph between logk versus 1/T is a straight line.
View SolutionA graph plotted between log10Kc and 1/T is straight line with intercept 10 and slpoe equal t0 0.5. Calculate :
(i) pre -exponential factor A.
(ii) heat of reaction at 298K.
(iii) equilibrium constant at 298K.
(iv) equilibrium constant in at 800k assuming ΔH remains constant in between 298K and 800K.View Solution
Knowledge Check
- Question 1 - Select One
The graph between the log K versus 1T is a straight line. The slope of the line is
A−2.303REaB−Ea2.303RC2.303REaDEa2.303R - Question 2 - Select One
For a reaction having rate constant k at a temperature T, when a graph between ln k and 1/T is drawn a straight line is obtained. The point at which line cuts y -axis and x -axis respectively correspond to the temperature:
A0,Ea2.303RlogAB∞,EaR ln AC0,logADNone of these. - Question 3 - Select One
For a hypothetical reaction: A(g)+B(g)⇔C(g)+D(g) a graph between log Keq and T− is striaght line as follows, where θ=tan−10.5 and OA=1.0 (S.I. units) Assuming ΔH∘ is independent of temperature, the equilibrium constant at 298 K will be:
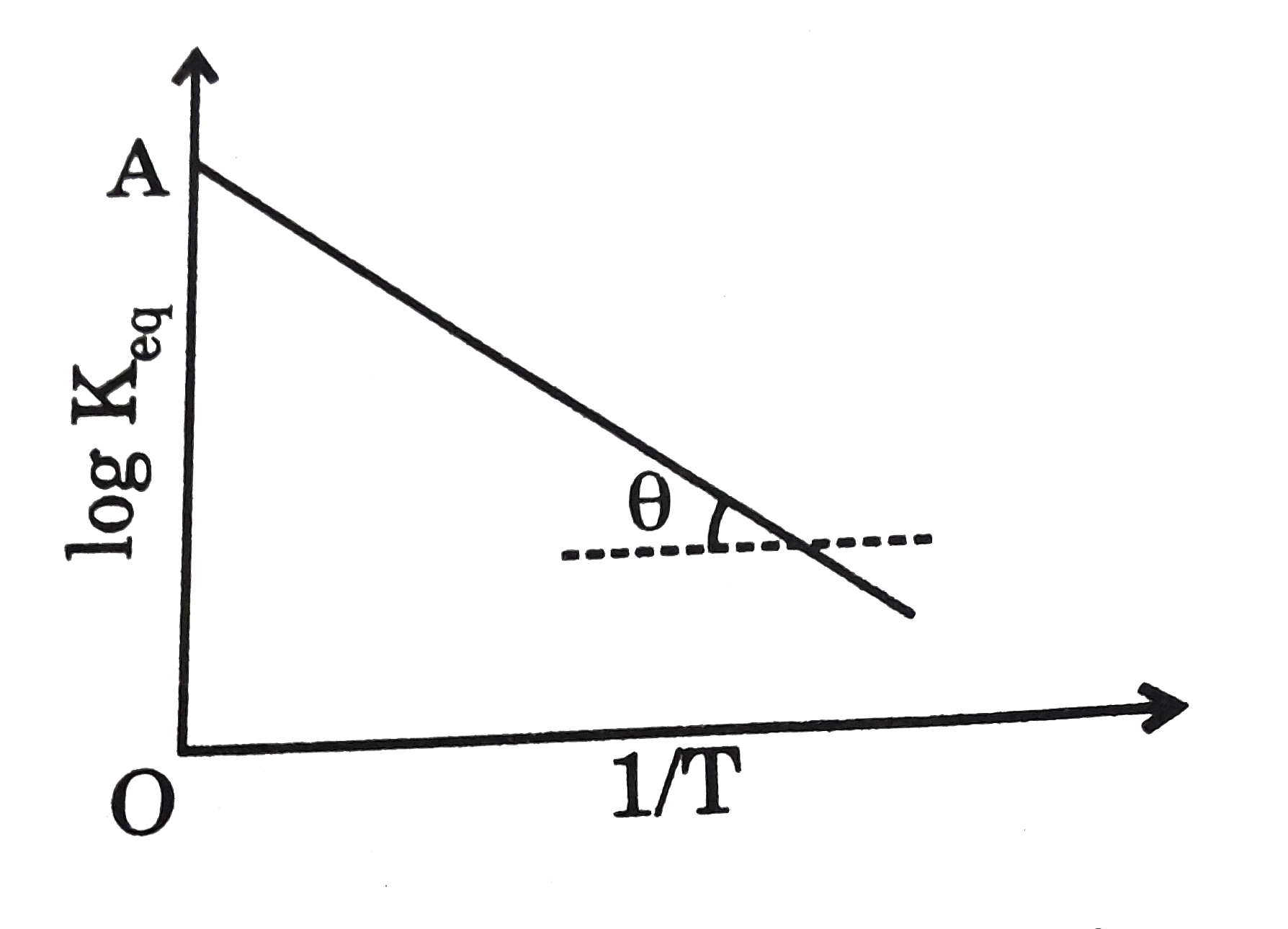 A10.002×109B3.79×108C7.96×109D9.96×109
A10.002×109B3.79×108C7.96×109D9.96×109
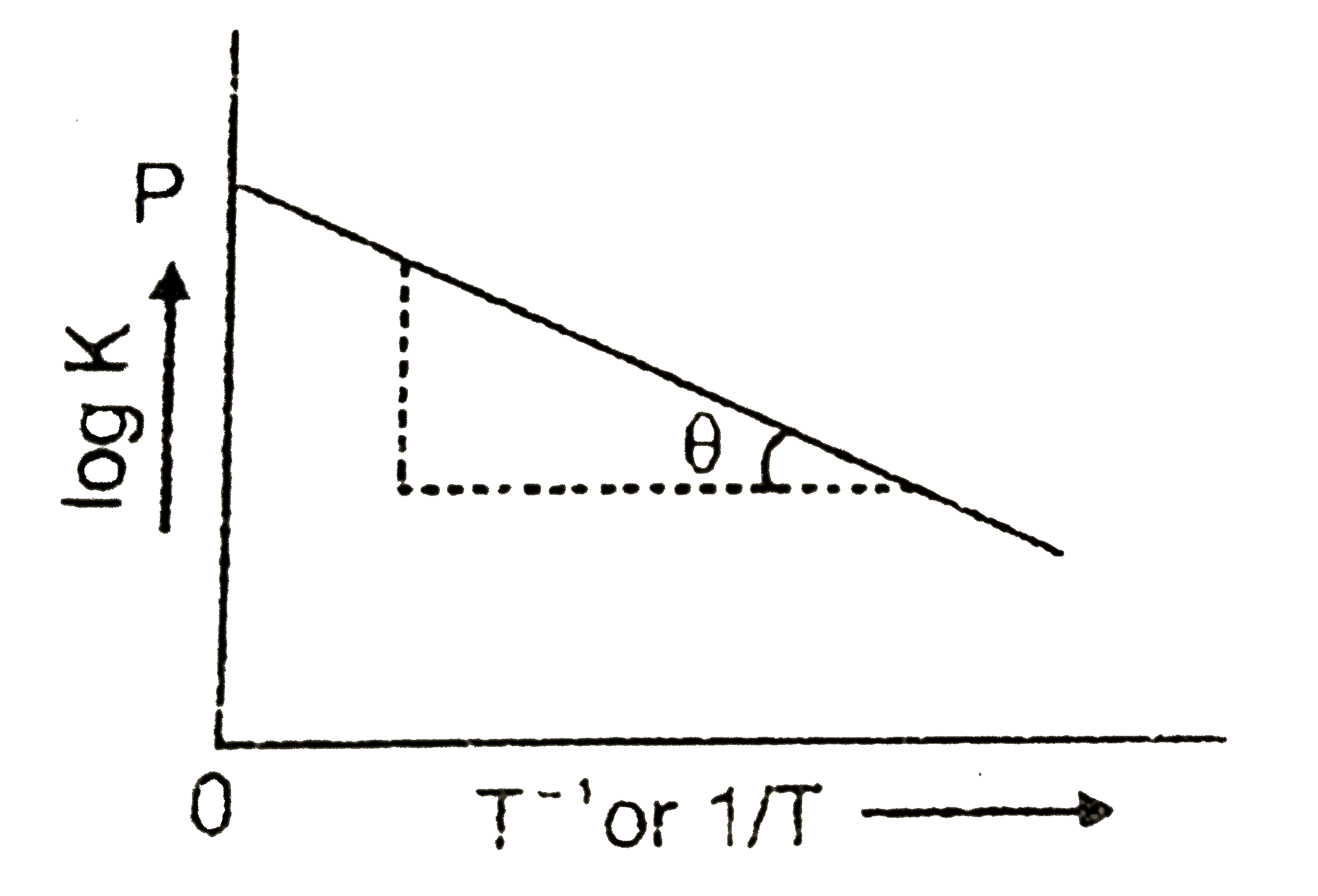
Variation of equiibrium constant K with temperature T is given by van 't Holf equation,
logK=logA−ΔH∘2.303RT
A graph between log K and T−1 was a straight line as shown in the figure and having θ=tan−1(0.5)andOP=10. Calculate:
(a) ΔH∘ (standard heat of reaction)when T=300K,
(b) A (pre-exponetial factor),
(c) Equilibrium constant K at 300K,
(d) Kat900KifΔH∘ is independent of temperature.
 View Solution
View SolutionWhen a graph between log K and 1/T is drawn a straight line is obtained. The point at which line cuts y-axis and x-axis respectively correspond to the temperature :
View SolutionA graph plotted between log k vs 1T is represented by
View SolutionMatch the following :−
List-I List -II
(P) Plot of lot t1/2 vs log[A0] is a straight line with a slope of '-1' (1) Zero order
( Q ) Plot of log t1/2 vs log[A0] is a straight line with a slope of '1' (2) 2nd order
( R ) Plot of log Kp vs 1/T is a straight line with a negative slope (3) ΔH∘ is negative
( S ) Plot of log Kp vs 1/T is a straight line with a positive slope (4) ΔH∘ is positiveView SolutionIn accordance to Arrhenius equation, the plot of log k against 1T is a straight line. The slope of the line is equal to
View Solution

