Ratio of ΔTb/Kbof6%AB2and9%A2BAB2andA2B both are non-electrolytes is 1 mol/kg in both cases. Hence atomic masses of A and B are respetively.
60,90
40,40
40,10
10,40
The correct Answer is:C
To solve the question regarding the ratio of ΔTb/Kb for the solutions of 6% AB₂ and 9% A₂BAB₂, we need to follow these steps:
Step 1: Understand the Problem
We are given two solutions:
1. 6% AB₂
2. 9% A₂BAB₂
Both solutions are non-electrolytes and have the same molality (1 mol/kg). We need to find the atomic masses of A and B based on the ratio of their boiling point elevation constants.
Step 2: Define the Boiling Point Elevation Formula
The boiling point elevation can be expressed using the formula:
ΔTb=i⋅Kb⋅m
where:
- ΔTb = boiling point elevation
- i = van 't Hoff factor (number of particles the solute breaks into)
- Kb = ebullioscopic constant of the solvent
- m = molality of the solution
Step 3: Calculate the Van 't Hoff Factor (i)
For non-electrolytes, the van 't Hoff factor i is equal to 1. Thus, for both solutions:
- For 6% AB₂: i=1
- For 9% A₂BAB₂: i=1
Step 4: Set Up the Ratio
Given that the ratio of ΔTb/Kb for both solutions is equal to 1, we can set up the following equation:
ΔTb1Kb1=ΔTb2Kb2
Step 5: Express the Boiling Point Elevation
Using the boiling point elevation formula:
ΔTb1=Kb1⋅m
ΔTb2=Kb2⋅m
Since both solutions have the same molality (1 mol/kg), we can simplify the ratio:
Kb1Kb2=6%9%
Step 6: Calculate the Ratio
Now, substituting the percentages:
Kb1Kb2=69=23
Step 7: Relate to Molar Mass
The boiling point elevation constant Kb is related to the molar mass of the solute. Therefore, we can set up the relationship:
MAMB=23
Step 8: Solve for Atomic Masses
Let the atomic mass of A be MA and that of B be MB. From the ratio, we can express:
MA=23MB
Step 9: Conclusion
To find the specific atomic masses, we would need additional information or constraints (like the total mass of the solute). However, based on the ratio derived, we can conclude that the atomic masses of A and B are related as MA:MB=2:3.
We are given two solutions:
1. 6% AB₂
2. 9% A₂BAB₂
The boiling point elevation can be expressed using the formula:
ΔTb=i⋅Kb⋅m
where:
- ΔTb = boiling point elevation
- i = van 't Hoff factor (number of particles the solute breaks into)
- Kb = ebullioscopic constant of the solvent
- m = molality of the solution
For non-electrolytes, the van 't Hoff factor i is equal to 1. Thus, for both solutions:
- For 6% AB₂: i=1
- For 9% A₂BAB₂: i=1
Given that the ratio of ΔTb/Kb for both solutions is equal to 1, we can set up the following equation:
ΔTb1Kb1=ΔTb2Kb2
Using the boiling point elevation formula:
ΔTb1=Kb1⋅m
ΔTb2=Kb2⋅m
Kb1Kb2=6%9%
Now, substituting the percentages:
Kb1Kb2=69=23
The boiling point elevation constant Kb is related to the molar mass of the solute. Therefore, we can set up the relationship:
MAMB=23
Let the atomic mass of A be MA and that of B be MB. From the ratio, we can express:
MA=23MB
To find the specific atomic masses, we would need additional information or constraints (like the total mass of the solute). However, based on the ratio derived, we can conclude that the atomic masses of A and B are related as MA:MB=2:3.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - LIQUID SOLUTION EXERCISE - REASONING TYPE QUESTIONS5videos
LIQUID SOLUTION
- BOOK - FIITJEECHAPTER - LIQUID SOLUTION EXERCISE - COMPREHENSION3videos
LIQUID SOLUTION
- BOOK - FIITJEECHAPTER - LIQUID SOLUTION EXERCISE - SOLVED PROBLEMS (SUBJECTIVE)17videos
LIQUID SOLUTION
- BOOK - FIITJEECHAPTER - IONIC EQUILIBRIUM EXERCISE - SINGLE INTEGER ANSWER QUESTIONS4videos
IONIC EQUILIBRIUM
- BOOK - FIITJEECHAPTER - NUCLEIC ACID AND VITAMIN EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE)15videos
NUCLEIC ACID AND VITAMIN
Similar Questions
Ratio of ΔTbKb of 10 g AB2 and 14g A2B per 100 g of solvent in their respective, solution (AB2 and A2B both are non-electrolytes) is 1 mol/kg in both cases. Hence, atomic wt. of A and B are respectively.
View SolutionAB2 and A2B3 are two compounds of the elements A and B 0.15 mole of each of these compounds weights 9.3and 15.9g respectively. Find the atomic masses of A and B.
View Solution
Knowledge Check
- Question 1 - Select One
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Ratio of ΔTb/Kb of 6%AB2 and 9%A2B(AB2 and A2B both are non-electrolytes) is 1 mol/kg in both cases. Hence, atomic masses of A and B are respectively.A60,90B40,40C40,10D10,40 - Question 2 - Select One
Ratio of ΔTb/Kb for 6%AB2and9%A2B(AB2andA2B both are non-electrolytes ) is 1 mol/kg in both cases. Hence , atomic masses of A and B are respectively :
A60, 90B40 , 40C40 , 10D10 , 40 - Question 3 - Select One
Let →a=a1ˆi+a2ˆj+a3ˆk,→b=b2ˆj+b3ˆkand→c=c1ˆi+c2ˆj+c3ˆk gve three non-zero vectors such that →c is a unit vector perpendicular to both →aand→b. If the angle between →aand→bisπ6, then prove that ∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣p=14(a21+a22+a23)(b21+b22+b23)
A0B1C14Σa21.Σb21D34Σa21.Σb21.Σa21
if Δ=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣
View SolutionA mixture of AB3(g) and A2B4(g) is placed in a sealed container. (At. Mass of A = 14 and At. ,mass of B =1 )
The temperature initially maintained is 300K. The total pressure is 0.5 atm. The container is heated to 1200k, when both AB3 and A2B4 decomposed to A2 and B2 when the decomposition was complete the pressure observed was 4.5 atm.
What is the percentage of AB3(g) in the original mixture ?View SolutionIn the figure, if B1,B2,B3, and A1,A2,A3,….. have been marked at equal distances. In what ratio C divides AB?
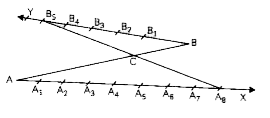 View Solution
View Solutionvan't Hoff factor of an electrolyte A2B3 assuming that it ionizes 75% in the solution is
View SolutionA2+2B2→A2B4
32A2+2B2→A3B4
Two substance A2&B2 react in the above manner when A2 is limited it gives A2B4 in excess gives A3B4.A2B4 can be converted to A3B4 when reacted with A2. Using this information calculate the composition of the final mixture when the mentioned amount of A%B are taken :c
(a)4 mole A2&4mole B2
(b)12 moles A2&2 moles B2
(c)1.25 moles A2&2 moles B2View Solution

