Question

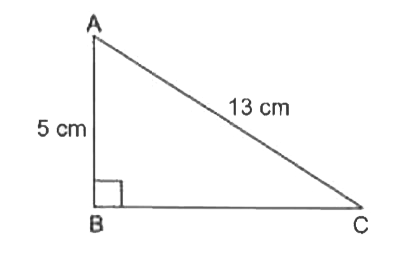
In $\Delta ABC,\angle B={90}^{\circ },BC=5cm$ and AC - AB = 1 cm. Find the value of sinC and cos C.

Answer

`sin C = ( 12)/( 13)`
`cos C = ( 5)/( 13)`

Explanation

To solve the problem step by step, we will analyze the given information and apply the Pythagorean theorem to find the values of sin C and cos C.

Step 1: Understand the triangle and given information
We have a right triangle ABC where:
- Angle B = 90°
- Side BC = 5 cm
- AC - AB = 1 cm

Step 2: Define the sides
Let:
- AB = x cm
- AC = x + 1 cm (since AC - AB = 1 cm)

Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem, in a right triangle:
\( AC^2 = AB^2 + BC^2 \)
Substituting the values we have:
\( (x + 1)^2 = x^2 + 5^2 \)

Step 4: Expand and simplify the equation
Expanding the left side:
\( x^2 + 2x + 1 = x^2 + 25 \)
Now, we can simplify this equation by subtracting \( x^2 \) from both sides:
\( 2x + 1 = 25 \)

Step 5: Solve for x
Now, isolate x:
\( 2x = 25 - 1 \)
\( 2x = 24 \)
\( x = 12 \)

Step 6: Find the lengths of AB and AC
Now that we have x:
- AB = x = 12 cm
- AC = x + 1 = 12 + 1 = 13 cm

Step 7: Calculate sin C
The sine of angle C is given by the ratio of the opposite side (AB) to the hypotenuse (AC):
\( \sin C = \frac{AB}{AC} = \frac{12}{13} \)

Step 8: Calculate cos C
The cosine of angle C is given by the ratio of the adjacent side (BC) to the hypotenuse (AC):
\( \cos C = \frac{BC}{AC} = \frac{5}{13} \)

Final Answers
- \( \sin C = \frac{12}{13} \)
- \( \cos C = \frac{5}{13} \)

---