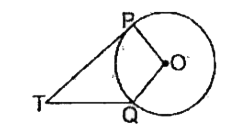
Two tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
Step by step video, text & image solution for Two tangents T P and T Q are drawn to a circle with centre O from an external point T . Prove that /_P T Q=2/_O P Q . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRACTICE TEST-1 BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE TEST-1 EXERCISE - SECTION-B
7 Videos
- PRACTICE PAPER- I (WITH SOLUTIONS) CLASS: X Mathematics (Standard)BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE PAPER- I (WITH SOLUTIONS) CLASS: X Mathematics (Standard)EXERCISE - SECTION -D
6 Videos
- PRACTICE TEST-IIBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE TEST-IIEXERCISE - Section C
14 Videos
Similar Questions
Knowledge Check
Two tangents PA and PB are drawn to a circle with centre O from an external point P. If ∠OAB=30∘, then ∠APB is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि ∠OAB=30∘ है, तो ∠APB का मान क्या होगा ?A15∘B30∘C120∘D60∘TP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ?
 ANoBYesCCannot sayDData insufficient
ANoBYesCCannot sayDData insufficient
Two circles touch externally at a point P . From a point T on the tangent at P , tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ=TR . (FIGURE)
View SolutionFrom an external point P, two tangents PAandPB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View SolutionIn the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT=30∘, prove that BA:AT =2:1
View SolutionIn Fig, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR=130∘ and S is a point on the circle, find ∠1+∠2.
View SolutionFrom any point P tangents of length t1 and t2 are drawn to two circles with centre A,B and if PN is the perpendicular from P to the radical axis and t21-t22=K.PN⋅AB then K=
View SolutionIf angle between two tangents drawn from a point P to a circle of radius 'a' and the centre O is 90∘ then prove that OP=√a
View Solution