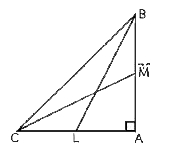
BL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM2)=5BC2
Step by step video, text & image solution for BL and CM are medians of a triangle ABC right angled at A. Prove that 4(B L^2+C M^2)=5B C^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRACTICE TEST-IIBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE TEST-IIEXERCISE - Section B
6 Videos
- PRACTICE TEST-1 BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE TEST-1 EXERCISE - SECTION-C
14 Videos
- PROBABILITYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROBABILITYEXERCISE - PRACTICE-TEST
11 Videos
Similar Questions
Knowledge Check
In a Δ right angled at B . AC = 5 cm , median AL=3√52 find the length of second median CM in cm ?
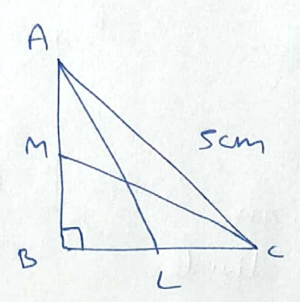 A2√5 cmB5√2 cmC10√2 cmD4√5 cm
A2√5 cmB5√2 cmC10√2 cmD4√5 cm
ABC is an isosceles right triangle right-angled at C . Prove that AB2=2AC2 .
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View SolutionIn ΔABC,∠BAC=90∘, seg BL and seg CM are median of ΔABC. Then prove that: 4(Bl2+Cm2)=5BC2
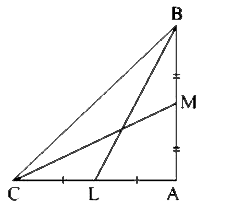
View Solutionseg AN and seg CM are the medians of △ABC in which ∠B=90∘ Prove that 4(AN2+CM2)=5AC2
View SolutionThe points A(2,9),B(a,5),C(5,5) are the vertices of a triangle ABC right angled at B . Find the value of a and hence the area of ABC.
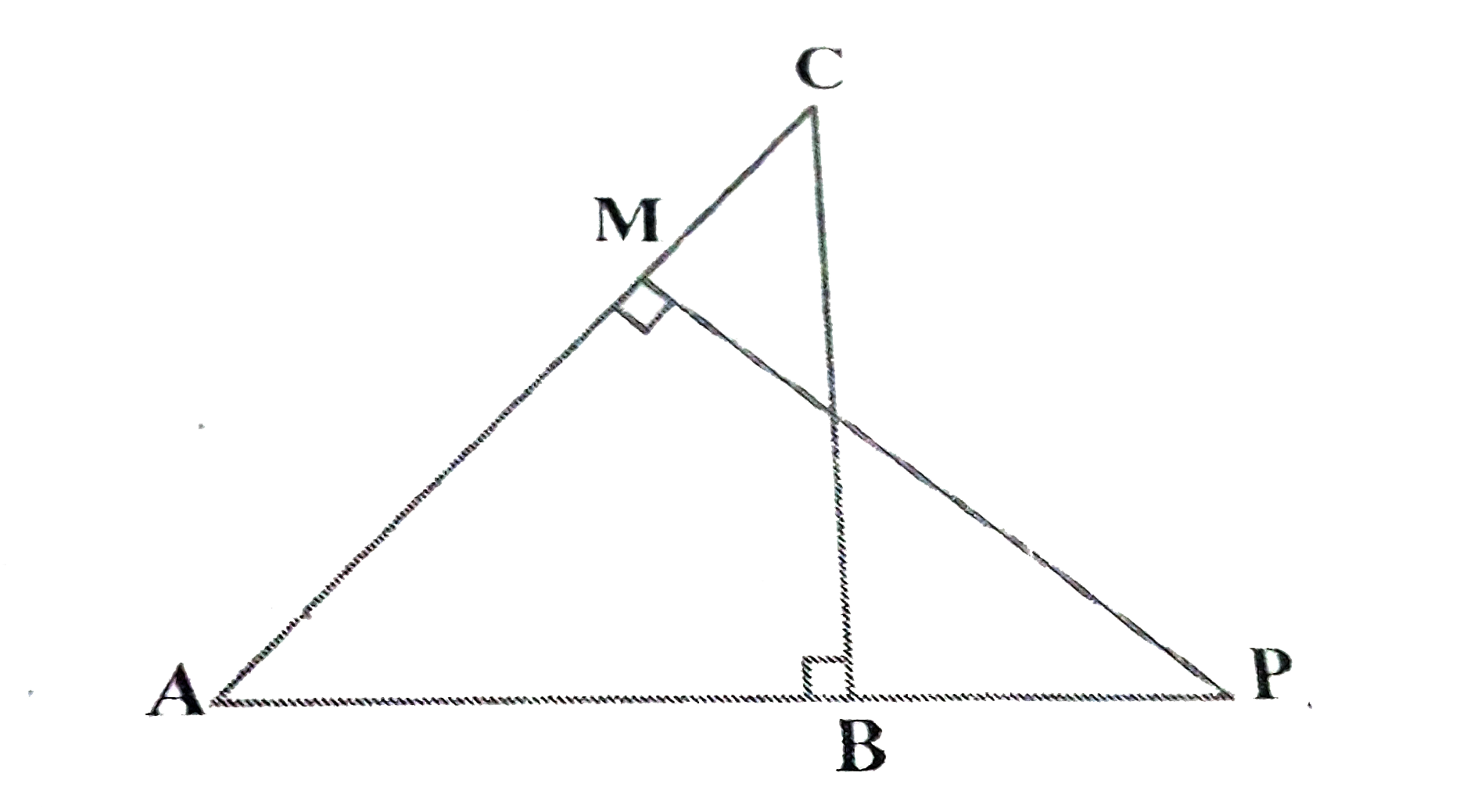
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
View Solution