A coin lies on the bottom of a lake 2m deep at a horizontal distance x from the spotlight (a source of thin parallel been of light) situated 1m above the surface of a liquid of refractive index μ=√2) and height 2m. Find x.
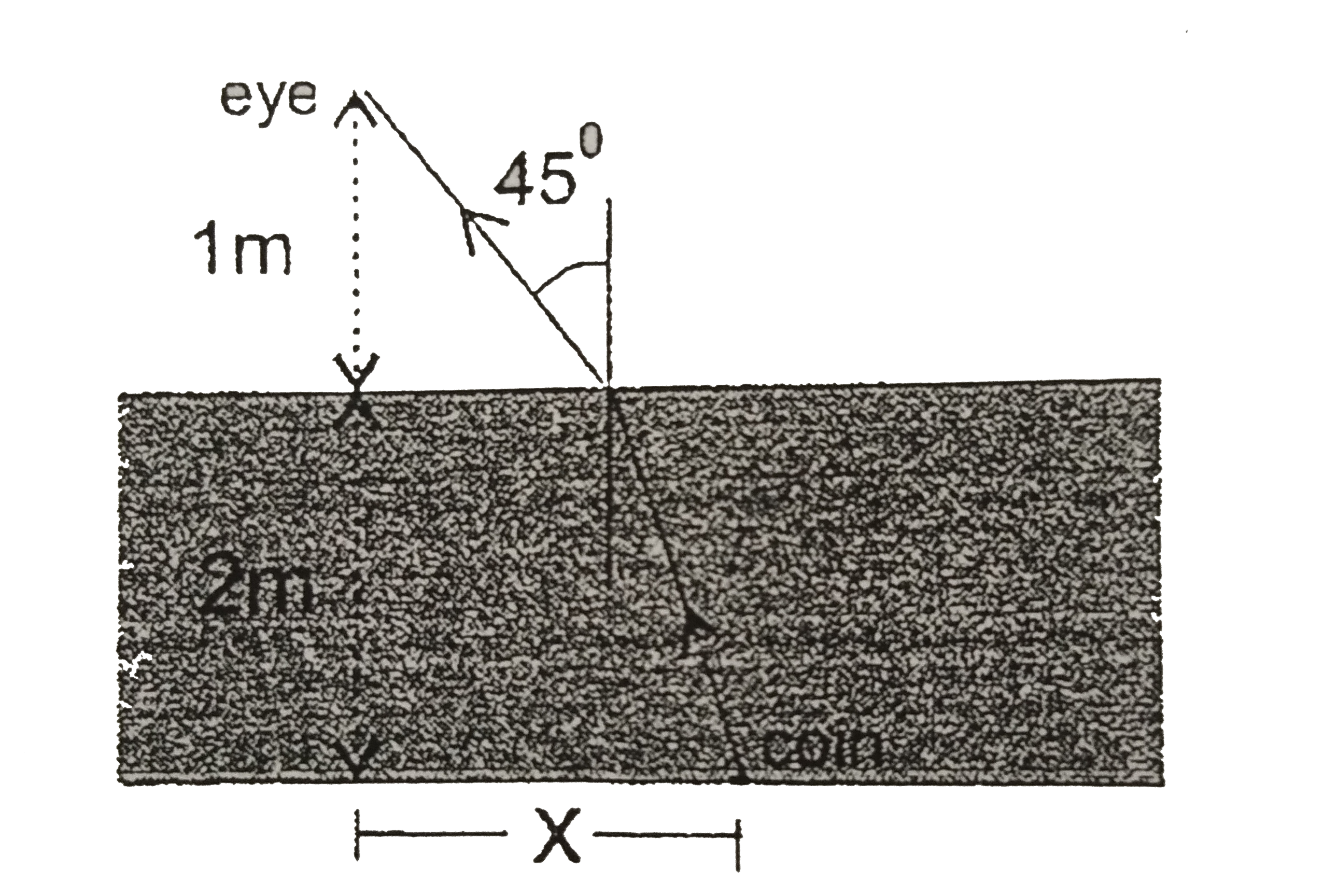
√2=sin45∘sinr
⇒sinr=12⇒r=30∘
x=RQ+QP
1m+2tan30∘m
=(1+2√3)m

Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1
142 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
63 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
A coin lies on the bottom of a lake 2 m deep at a horizontal distance x from the spot light S which is a source of thin parallel beam of light situated 1 m above the surface of the liquid of refractive index p= as shown in figure. The liquid height is 2m. Find x so that a narrow beam of light from S when incident on the liquid surface at incidence angle 45∘ fells directly on the coin

View SolutionA point source of light is placed at a distance h below the surface of a large and deep lake. If f is the fraction of light energy that escapes directly from water surface and μ is refractive index of water then:
View Solution
Knowledge Check
A double convex lens of refractive index m1 is immersed in a liquid of refractive index m2. This lens will act as:
Adiverging lens If m1>m2Bdiverging lens if m1<m2Cconverging lens if m1=m2Dconverging lens if m1<m2A fish lies at the bottom of a 4m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4/3 . Then the distance between
ABird and image of fish is 9mBFish and image of is 12mCFish and image of bird is 8mDFish and image of bird is 10mA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
A7.5cmB6.75cmC4.5cmD1.5cm
A stream of water escapes from a hole 2m above the Q. 1 base of a tank and strikes the ground at a horizontal distance of 6m .The depth of the hole from the free surface of water is
View SolutionA stream of water escapes from a hole 2m above the Q. 1 base of a tank and strikes the ground at a horizontal distance of 6m .The depth of the hole from the free surface of water is
View SolutionA pile 4m high driven into the bottom of a lake is 1m above the <br>water . Determine the length of the shadow of the pile on the bottom of the lake if <br> the sun rays make an angle of 45∘ with the water surface . The refractive index<br> if water is 43.
View SolutionConsider a tin can of height h as shown in the figure. A coin lies on the botttom at the centre. From the position shown you can barely see the far side of the bottom of the can. When the can is slowly filled with water of refractive index μ, coin is just visible when the can is full. Show that the ratio of the height to radius is
hr=2√μ2−14−μ2

View SolutionA disc is placed on a surface of pond which has refractive index 35 . A source of light is placed 4 m below the surface of liquid. The minimum radius of disc will be so light is not coming out
View Solution
