The image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
![The image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. mu of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure. As a result of this, in case of convergent lens if a screen is placed at F(v) center of the image will be violet and focused while sides are red and blurred. While at F(R) , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between f(v) and f(R) is a measure of the longitudinal chromatic aberration (L.C.A),i.e., L.C.A.=f(R)-f(v)=-df with df=f(v)-f(R) ...........(1) However, as for a single lens, (1)/(f)=(mu-1)[(1)/(R(1))-(1)/(R(2))] .............(2) rArr -(df)/(f^(2))=dmu[(1)/(R(1))-(1)/(R(2))] ...............(3) Dividing E1n. (3) by (2) : -(df)/(f)=(dmu)/((mu-1))=omega, [omega=(dmu)/((mu-1))]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_OPT_PHY_XII_C01_E01_133_Q01.png)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
Chromatic aberration in the formation of image by a lens arises because :
of non-paraxial rays.
the radil of curvature of the two sides are not same.
of the defect in grinding.
the focal length varies with wavelength.
The correct Answer is:D
N//a
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
79 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1
142 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
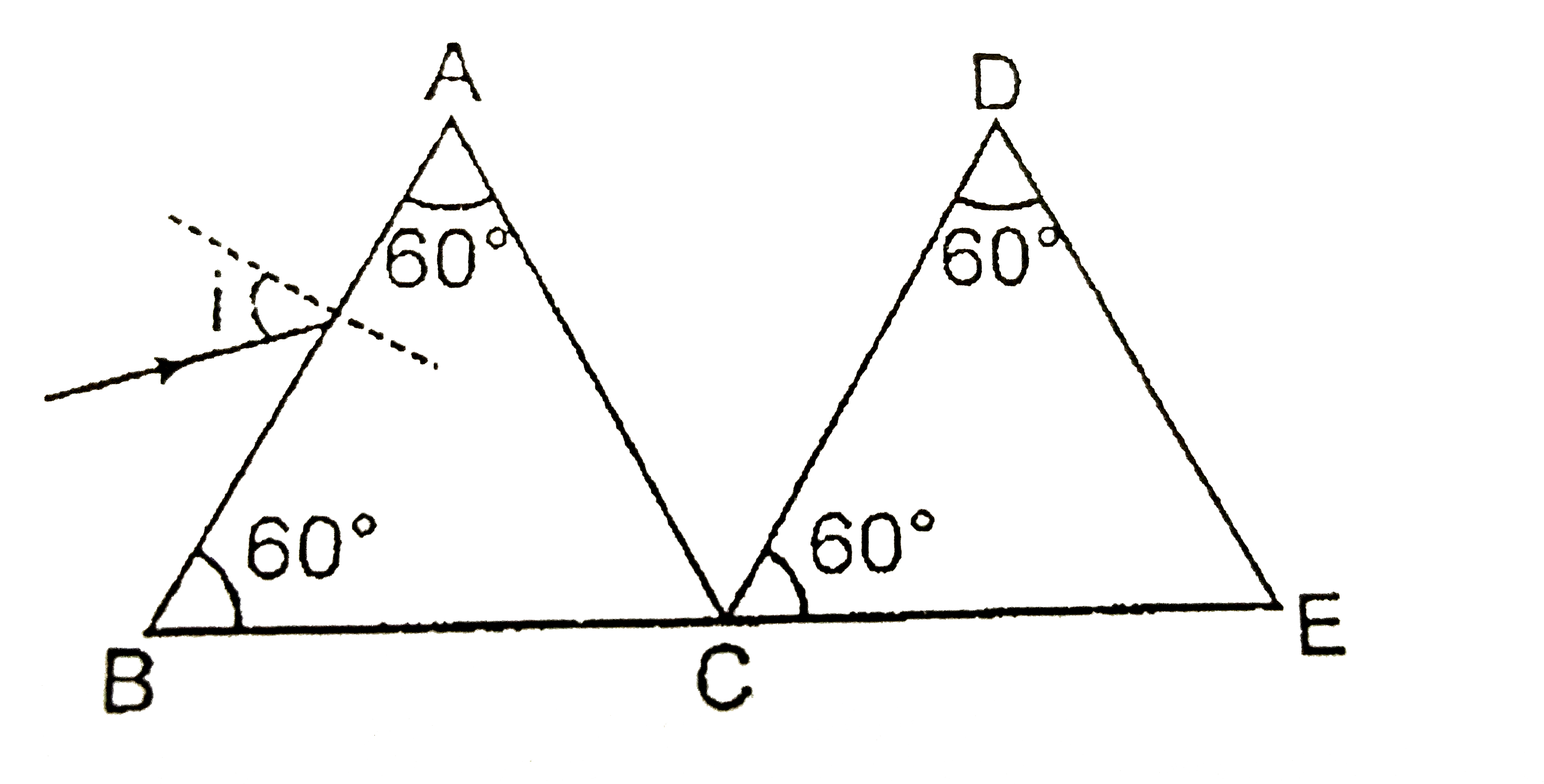
In the figure two triangular prism are shown each of refractive index √3 .
(a) Find the angle of incidence on the face AB for minimum deviation from the prism ABC ?
(b) Find the angle through which the prism DCE should be ratated about the edge passing through point C so that there should be minimum deviation from the system ?
View SolutionAU-shaped wire is placed before a concave mirror having radius of curvature 20cm as shown in figure. Find the total length of the image

View SolutionTwo plane mirros are inclined to each other at an angle 60∘ if a ray of light incident on firs tmirros paralell to the second mirror, it is reflected formt the second mirror
View SolutionTwo full turns of the circular scale of a screw gauge cover a distance of 1mm on its main scale. The total number of divisions on the circular scale is 50. Further, it is found that the screw gauge has a zero error of −0.03mm. While main scale reading of 3mm and the number of circular scale divisions in line with the main scale as 35. the dimeter of the wire is
View SolutionLet a star be much brighter than our sun but its mass is same as that of sun If our earth has average lift span of man as 70years In the earth like planet of this star system having double the distance from our star find the average lift span of a man on this planet in terms of our year
 .
.
View SolutionLet f_(v) and f_(r) are the focal lengths of a convex lens for violet and red lights respectively. If F_(v) and F_(r) are the focal lengths of a concave lens for violet and red light respectively, then
View SolutionChromatic aberrations in the formation of image by a lens arise becauses
View SolutionAssertion:- If an object placed on the optic axis of a lens is illuminated by white light, then image formed will be coloured and not exactl white. Reason:- The lens has different focal length sfor different colours.
View SolutionIf f(V) and fR are the focal lengths of a concex lens for violet and red light respectively and FVand FR are the focal lengths of concave lens for violet and red light respectively, then we have
View SolutionThe dispersive power of the material of a lens is 0.04 and the focal length of the lens is 10cm. Find the difference in the focal length (in mm) of the lens for violet and red colour.
View SolutionIf the focal length of a double convex lens for red light is f_(R) its focal length for the violet light is
View SolutionThe focal lengths of a thin convergent lens are 0.20m and 0.21m for voilet and red lights, respectively, An object is placed at a distance of 0.15m. Calculate the chromatic aberration in the image.
View SolutionThe focal length of a thin convex lens for red and violet colour are 44.6cm and 42.5cm. Calculate focal length for the mean colour and dispersive power of the lens.
View SolutionThe refractive indices of the material of a lens for violet, yellow and red colours of light are 1.66, 1.64 and 1.62 respectively. The mean focal length of the lens is 10 cm. What is the chromatic aberration of the lens between the violet and the red colours ?
View Solutionयदि लाल और बैंगनी किरणों के लिए एक उत्तल लेन्स की फ़ोकस दूरियाँ, क्रमश: 25 cm और 24 cm हों, तो लेन्स के पदार्थ का वर्णिक विपथन और परिक्षेपण क्षमता निकालें |
View SolutionFocal lengths of a lens for violet, yellow and red colours are f_(v), f_(y) and f_(r) respectively. Calculate the dispersive power of the material of the lens.
View Solution
