The dispersive power of the material of a lens is 0.04 and the focal length of the lens is 10cm. Find the difference in the focal length (in mm) of the lens for violet and red colour.
The correct Answer is:4
To solve the problem, we need to find the difference in the focal lengths of the lens for violet and red colors based on the given dispersive power and the focal length of the lens.
1. Understanding Dispersive Power:
The dispersive power (ω) is given by the formula:
ω=μv−μrμmean−1
where:
- μv is the refractive index for violet light,
- μr is the refractive index for red light,
- μmean is the mean refractive index.
Given that the dispersive power is 0.04, we can use this value in our calculations.
2. Using the Lens Maker's Formula:
The lens maker's formula relates the focal length f of a lens to its refractive index and radii of curvature:
1f=(μ−1)(1R1−1R2)
For small changes in refractive index, we can differentiate this equation.
3. Differentiating the Lens Maker's Formula:
We differentiate the lens maker's formula to find the change in focal length df with respect to the change in refractive index dμ:
df=dμ(μ−1)⋅1f2⋅(1R1−1R2)
However, since we are interested in the difference in focal lengths for violet and red light, we will focus on the changes in refractive index.
4. Calculating the Change in Focal Length:
We know that:
df=−10⋅(μv−μr)(μ−1)
Substituting the dispersive power:
df=−10⋅0.041=−0.4 cm
5. Converting to mm:
Since we need the answer in mm, we convert:
df=−0.4 cm×10=−4 mm
The negative sign indicates a difference, but we are interested in the magnitude:
Difference in focal length=4 mm
Final Answer:
The difference in the focal length of the lens for violet and red color is 4 mm.
The dispersive power (ω) is given by the formula:
ω=μv−μrμmean−1
where:
- μv is the refractive index for violet light,
- μr is the refractive index for red light,
- μmean is the mean refractive index.
The lens maker's formula relates the focal length f of a lens to its refractive index and radii of curvature:
1f=(μ−1)(1R1−1R2)
For small changes in refractive index, we can differentiate this equation.
We differentiate the lens maker's formula to find the change in focal length df with respect to the change in refractive index dμ:
df=dμ(μ−1)⋅1f2⋅(1R1−1R2)
However, since we are interested in the difference in focal lengths for violet and red light, we will focus on the changes in refractive index.
We know that:
df=−10⋅(μv−μr)(μ−1)
Substituting the dispersive power:
df=−10⋅0.041=−0.4 cm
Since we need the answer in mm, we convert:
df=−0.4 cm×10=−4 mm
The negative sign indicates a difference, but we are interested in the magnitude:
Difference in focal length=4 mm
The difference in the focal length of the lens for violet and red color is 4 mm.
Topper's Solved these Questions
Similar Questions
Find the focal length of the lens used.
View SolutionFind the focal length of the lens shown in Fig.
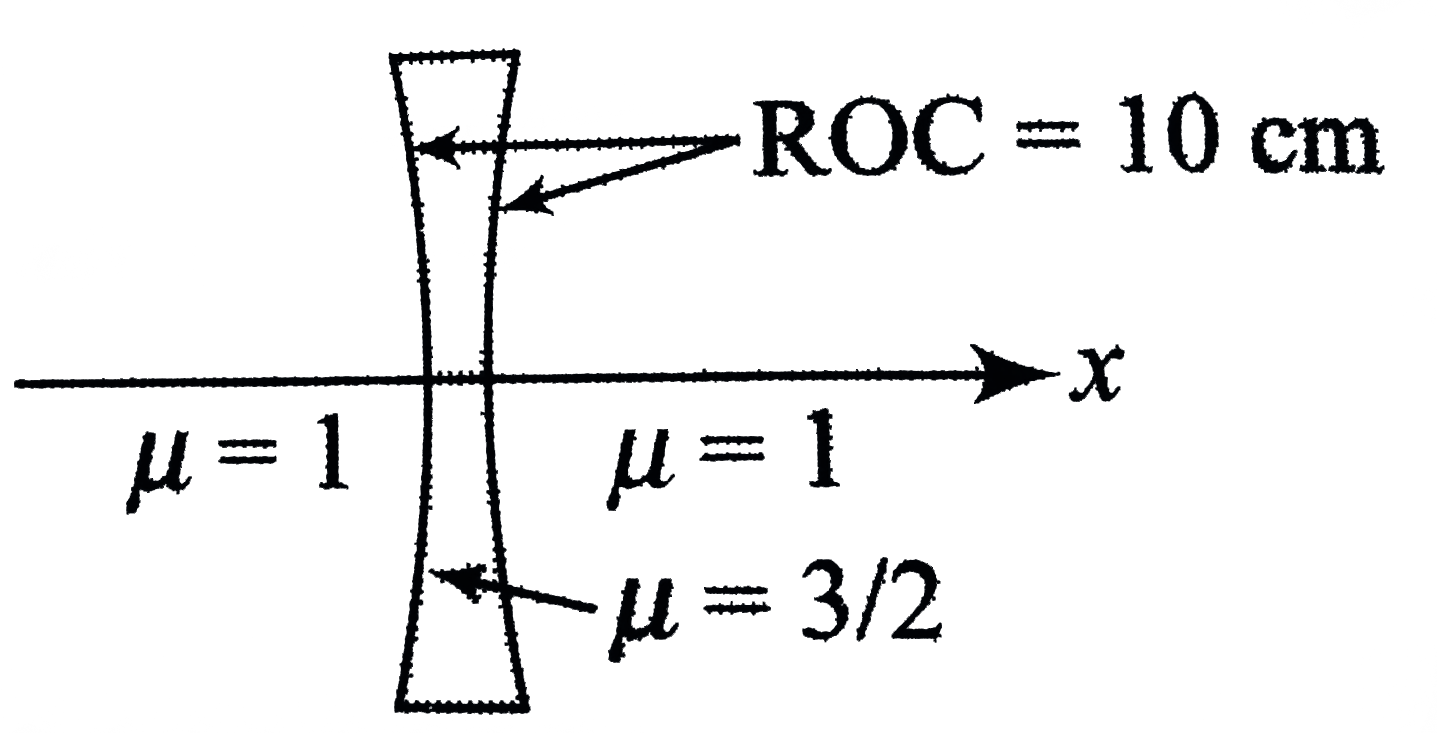 View Solution
View SolutionFind the focal length of the lens shown in the Fig..
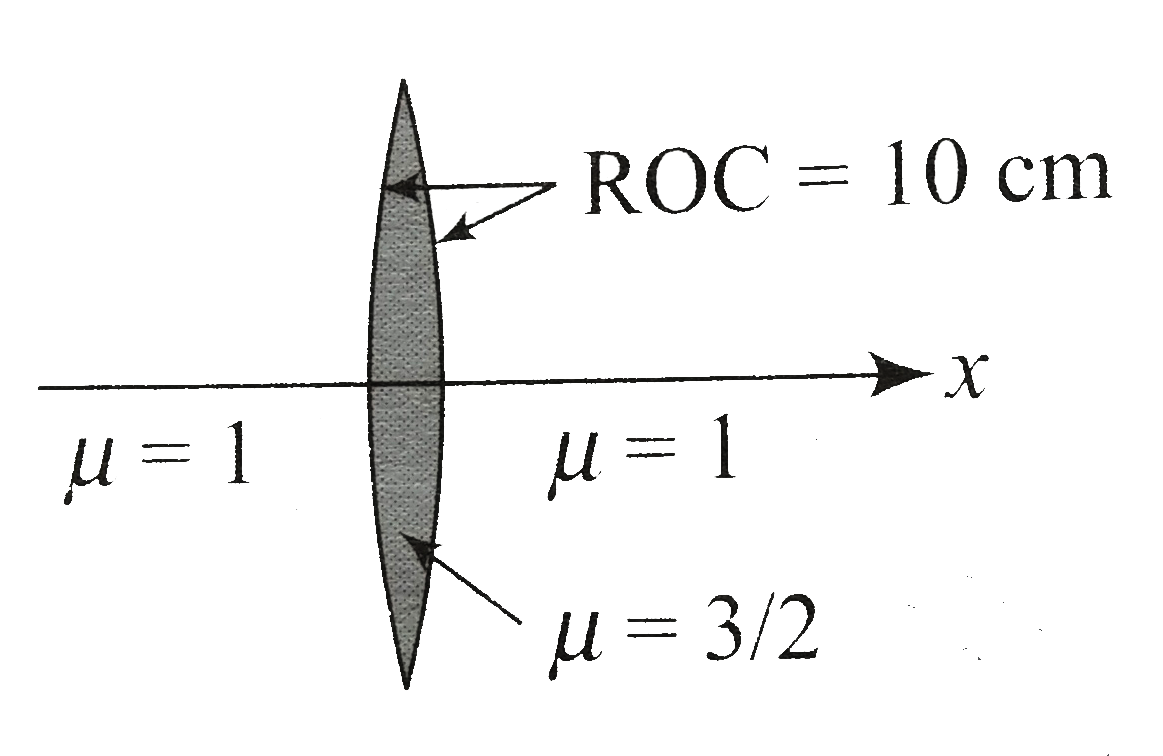 View Solution
View SolutionThe power of a lens is -5 D.
Find its focal length.View SolutionIf the focal length of the lens is 20 cm, find the distance of the image from the lens in the following figure?
 View Solution
View SolutionA focal length of a lens 10cm. What is power of a lens in dipotre?
View SolutionIf the focal length of objective lens is increased then magnifying power of
View SolutionFind the power of a concave lens of focal length 2m.
View SolutionIf the focal length of the objective lens is increased then Magnifying power
View SolutionThe focal length of a plano-concave lens is -10 cm , then its focal length when its palne surface is polished is
View Solution

