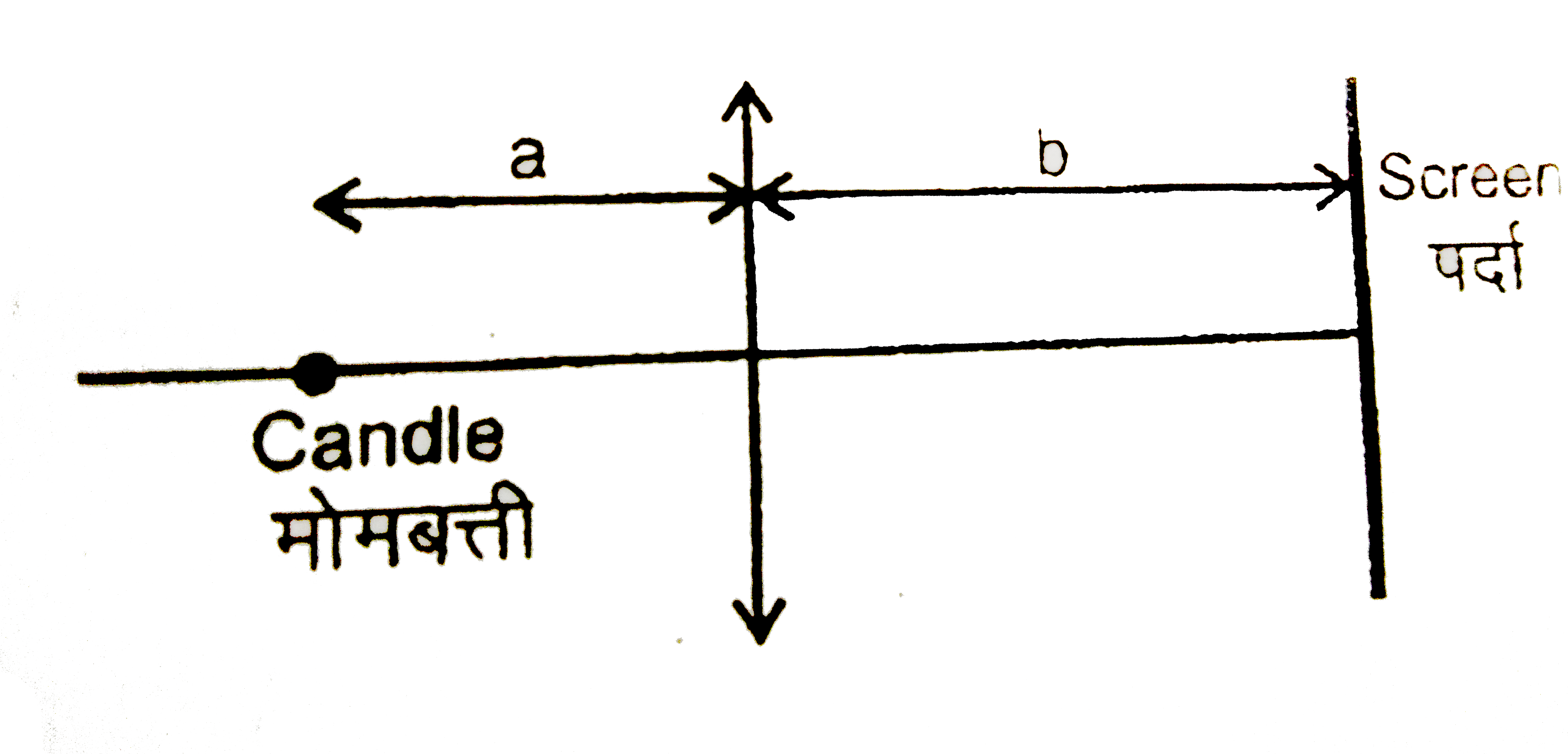
A convex lens produces an image of a condle flame upon a screen whose distance from candle is D. When the lens is displaced through a distance x, (the distance between the candle and the screen is kept constant), it is found that a sharp image is again produced upon the screen. Find the focal length of the lens in terms of D and x .
The correct Answer is:f=(D2−x2)/4D
a+b=Db−a=x2b=D+x
b=(D+x)/2a=(D−x)/2
1b−1−a=1f⇒2D+x+2D−x=1f
_(2).(D-x+D+x)/(D^(2)-x^(2))=(1)/(f) rArr(4D)/(D^(2)-x^(2))=(1)/(f) rArr f=(D^(2)-x^(2))//4D Ans.]
Topper's Solved these Questions
Similar Questions
A convex lens produces an image of a real object on a screen with a magnification of 1/2. When the lens is moved 30 cm away from the object, the magnification of the image on the screen is 2. The focal length of the lens is
View SolutionA convex lens of focal length f is placed somewhere in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal lnegth oof the lens is .
View Solution
Knowledge Check
A convex lens produces an image of a real object on a screen with a magnification of 1/2. When the lens is moved 30 cm away from the object, the magnification of the image on the screen is 2. The focal length of the lens is
A30 cmB60 cmC20 cmD15 cmA convex lens of focal length f is placed somewhere, in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal length of the lens is
Amx(m+1)2Bmx(m−1)2C(m+1)2mxD(m−1)2mxA convex lens of focal length f is placed somewhere in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal lnegth oof the lens is .
Amx(m+1)2Bmx(m−1)2C(m+1)2mxD(m−1)2mx
A convex lens forms an image of an object on a screen 30 cm from the lens. When the lens is moved 90 cm towards the object, then the image is again formed on the screen. Then, the focal length of the lens is
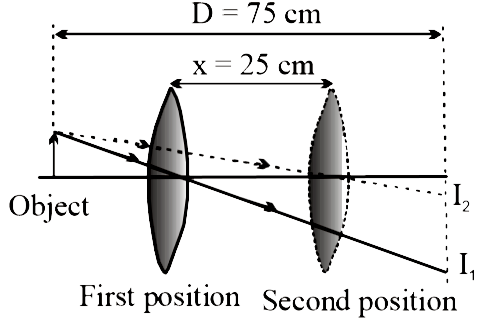
View SolutionA convex lens when placed in the first position forms a real image of an object on a fixed screen. The distance between the object and the screen is 75 cm. On displacing the lens from first position by 25 cm to the second position, again a real image is formed on the screen. Then the focal length of the lens is
View SolutionA convex lens forms an image of an object on a screen 30 cm from the lens. When the lens is moved 90 cm towards the object, then the image is again formed on the screen. Then, the focal length of the lens is
View SolutionA convex lens forms a real image on a screen placed at a distance 60 cm from the object. When the lens is shifted towards the screen by 20 cm , another image of the object is formed on the screen. The focal length of the lens is :
View SolutionAn object and a screen are mounted on an optical bench and a converging lens is placed between them so that a sharp image is obtained on the screen. The linear magnification of the image is 25. The lens is now moved 30 cm towards the screen and a sharp image is ■ again formed on the screen. Find the focal length of the lens
View Solution
