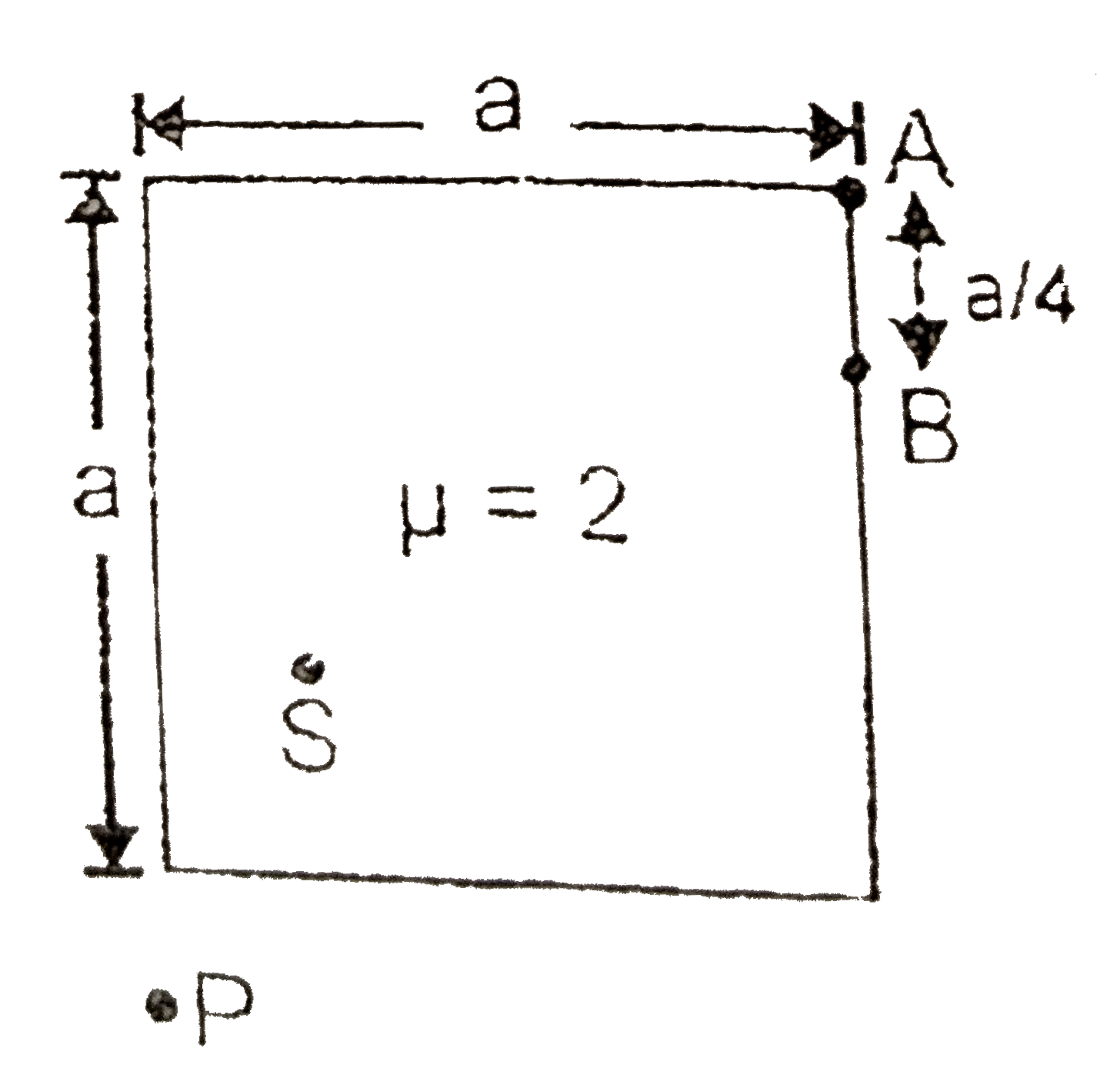
The figure shows the square face (of side 'a') of a transparent cuboidal block. The thickness or the third dimension of the block is negligible in comparison to 'a'. The block has uniform refrative index μ equal to 2. A point source S which can emit light in all directions can move inside the block. It is desired that no light of 'S' should pass through AB. Sketch the region in which S should be present to satisfy this condition.
The correct Answer is:(##RESOPTPHYXIIC01E01238_A01##)
sinC=12,C=30∘
If S is anywhere in the shaded region, the light rays from S will strike AB making an angle more than critical angle.

Topper's Solved these Questions
Similar Questions
An uncharge aluminium block has a cavity within it. The block is placed in a region where a uniform electric field is directed upward. Which of the following is a correct statement descrining conditions in the interior of the block's cavity?
View SolutionLight of wavelength 4500Å in vacuum enters into a glass block of refractive index 1.5. What is the wavelength of light in the glass block?
View Solution
Knowledge Check
A ray of light incident on a transparent block at an angle of incident 60∘. If the refractive index of the block is 1.732, the angle of deviation of the refracted ray is
A15∘B25∘C30∘D45∘An uncharge aluminium block has a cavity within it. The block is placed in a region where a uniform electric field is directed upward. Which of the following is a correct statement descrining conditions in the interior of the block's cavity?
AThe electric field in the cavity is directed upward.BThe electric field in the cavity is directed downward.CThere is no electric field in the cavity.DThe electric field in the cavity is of varying magnitude and is zero at the exact center.The reflected and refracted rays are observed to be perpendicular to each other, when ray of light is incident at an angle of 60∘ on a transparent block. The refractive index of the block is
A32B12C2√3D√3
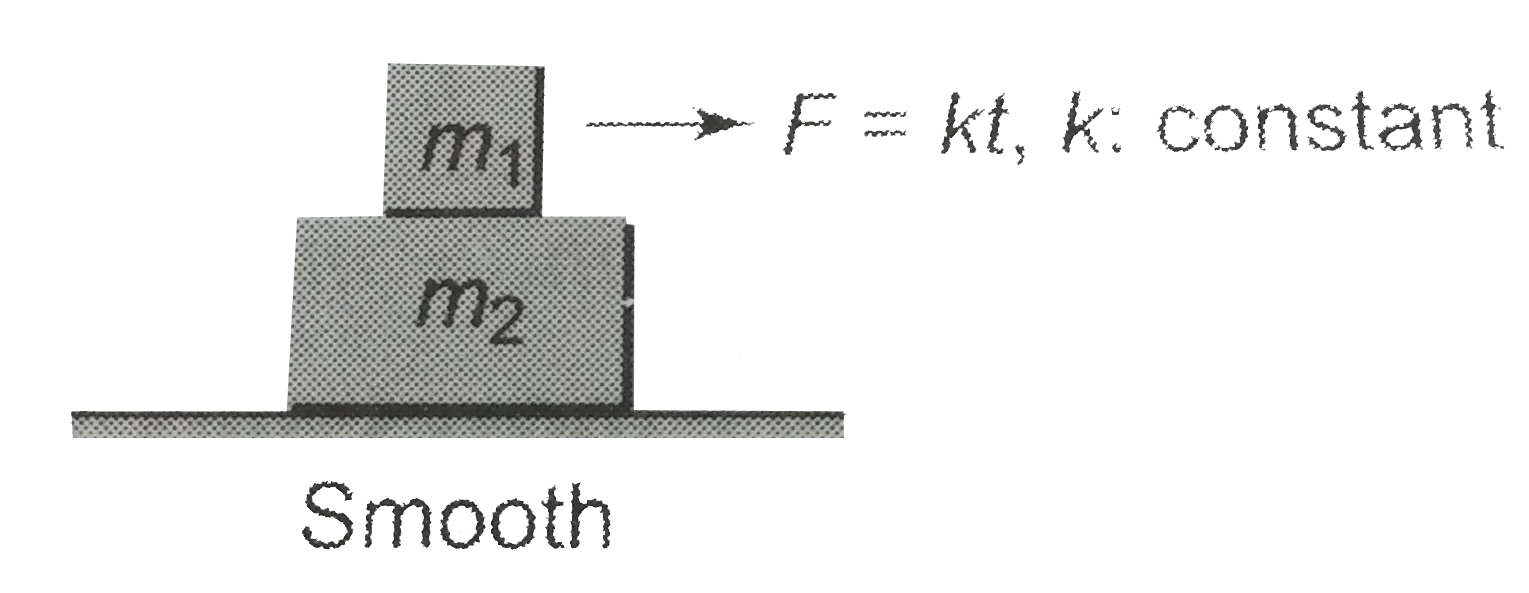
The friction coefficient between the blocks is μ. Sketch a graph showing variation of acceleration of the blocks will move separately.
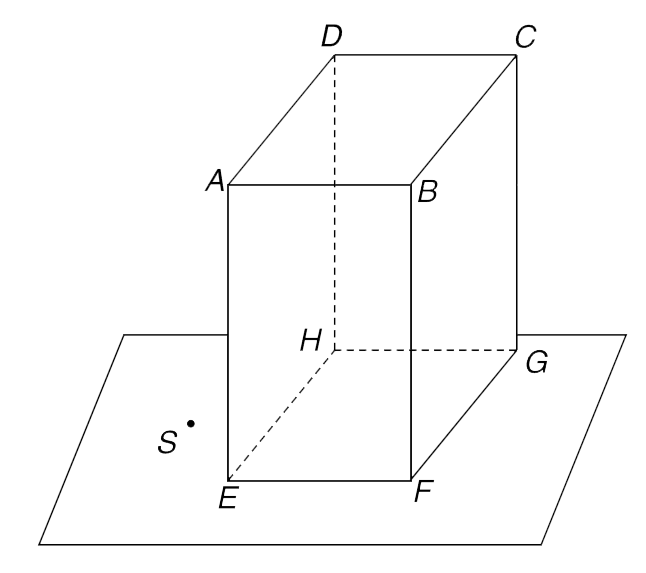
View SolutionA large rectangular glass block of refractive index μ is lying on a horizontal surface as shown in Figure. Find the minimum value of μ so that the spot S on the surface cannot be seen through top plane ‘ABCD’ of the block.
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horixontal plane. The cofficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horixontal plane. The cofficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View Solution
