Find the magnetic induction of the field at the point O at a loop with current I, whose shape is illustrated in figure
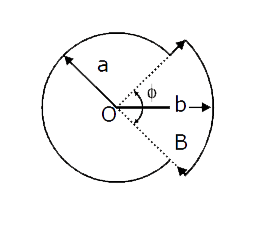
(a)In figure a the radii a and b, as well as the angle φ are known
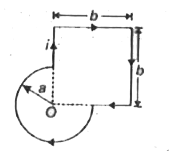
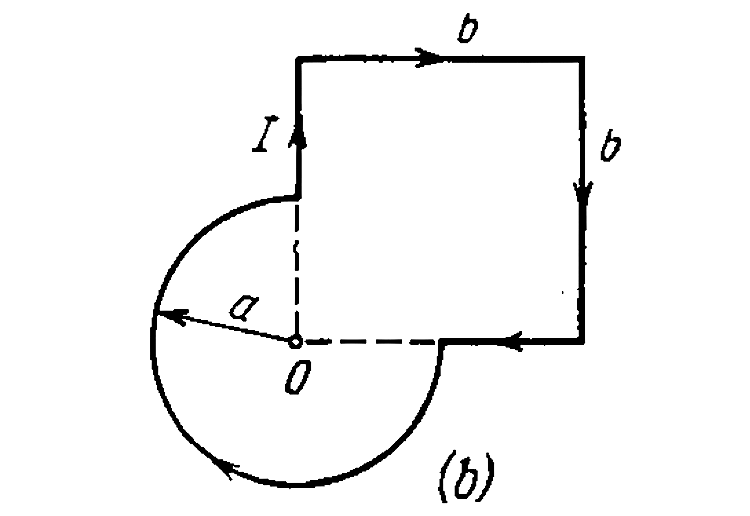
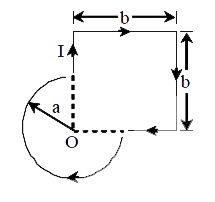
(b)In figure b,the raidus a and the side b are known.
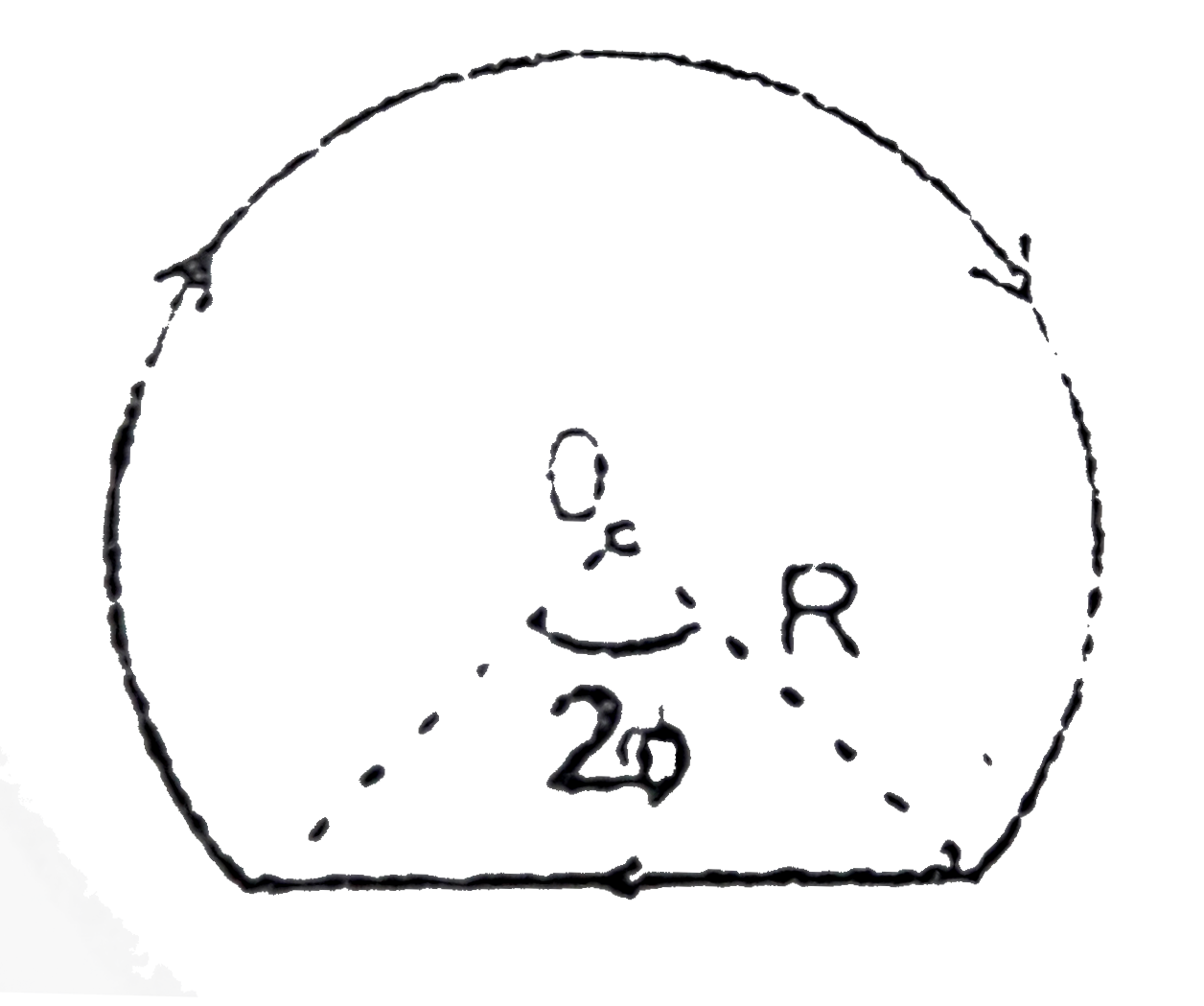
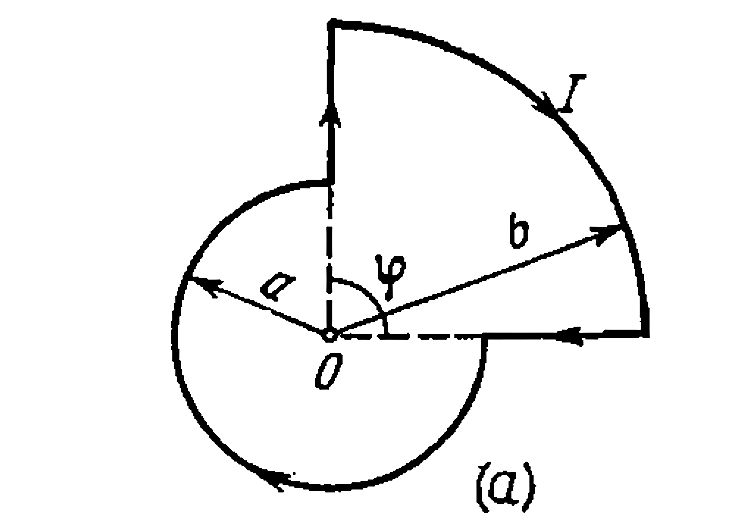
(c)A current I=5.0A flows along a thin wire shaped as shown in figure.The radius of a curved part of the wire is equal to R=120mm,the angle 2φ=90∘.Find the magnetic induction of the field at the point O.
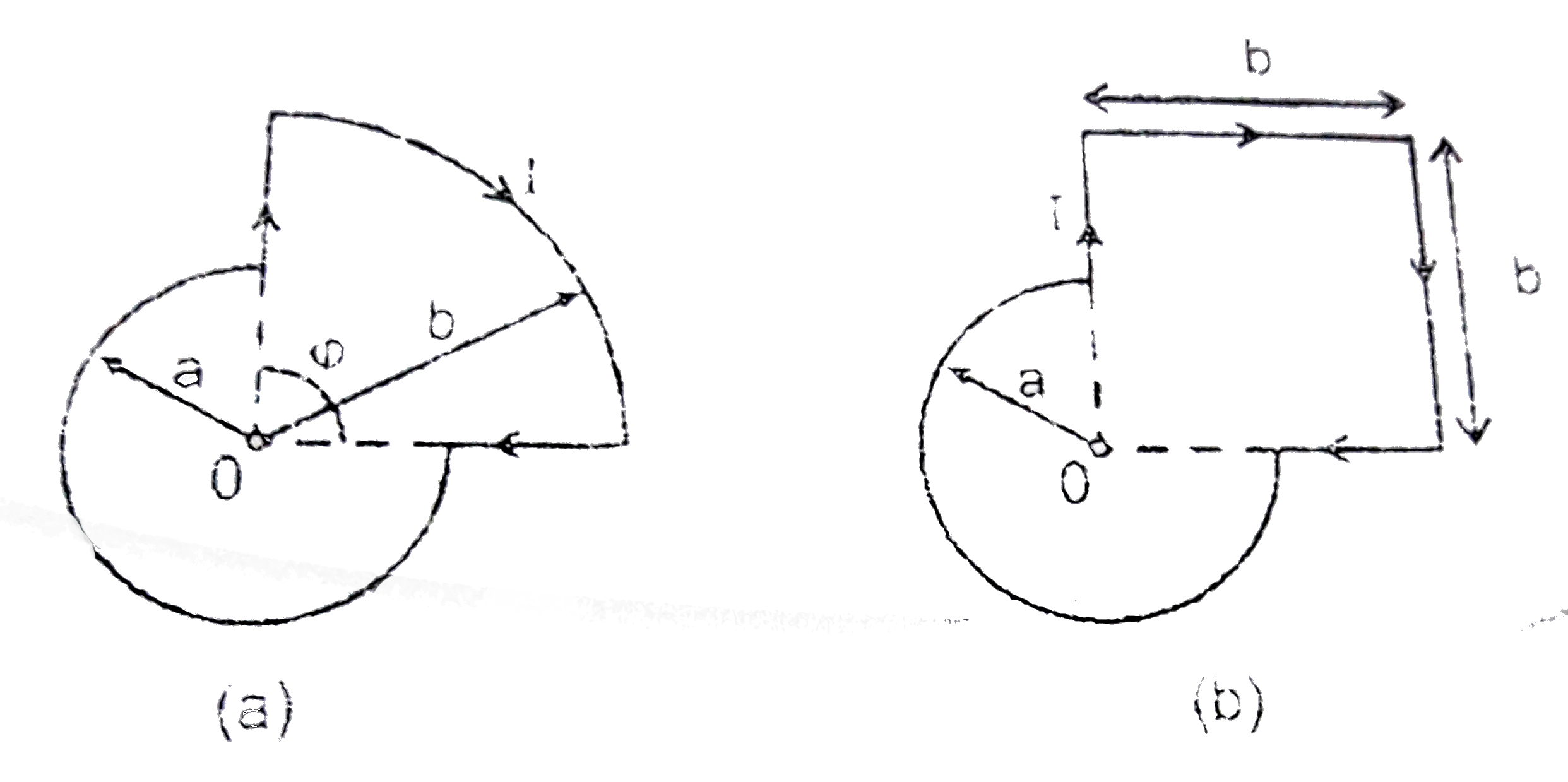
The correct Answer is:A, B, C, D
Bdue to st.part AB=0=Bdue to st.part CD
Bdue to curved part AD=(2π−ϕ2π)(μ0i2a) Into the plane of paper.
Bdue to curved part BC=ϕ2π(μ0i2b) Into the plane of paper.
BNet=μ0i4π[2π−ϕa+ϕb] Into the plane of paper.
(b)Bdue to BC=Bdue to EA=0
Bdue to curved part AB=3π22πμ0I2a⇒=38μ0la Into the plane of paper
Bdue to CD=μ0i4πb[cos90∘+cos45∘]⇒=μ0I4√2πb Into the paper
Bdue to DE=μ0I4√2πb Into the plane of paper
→BNet=μ0I4π[3π2a−√2b] Into the plane of paper.
(c) B=Bdue to st.part+Bdue to curved part both into the plane of paper
=(2π−2ϕ2π)μ0i2R+μ0i4πd[sinϕ+sinϕ]
=(2π−2ϕ2π)μ0i2R+μ0i4πRcosϕ[2sinϕ]
μ0i2πR[π−ϕ+tanϕ]=28μT


Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-2
54 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-1
15 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - PROBLEM
12 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
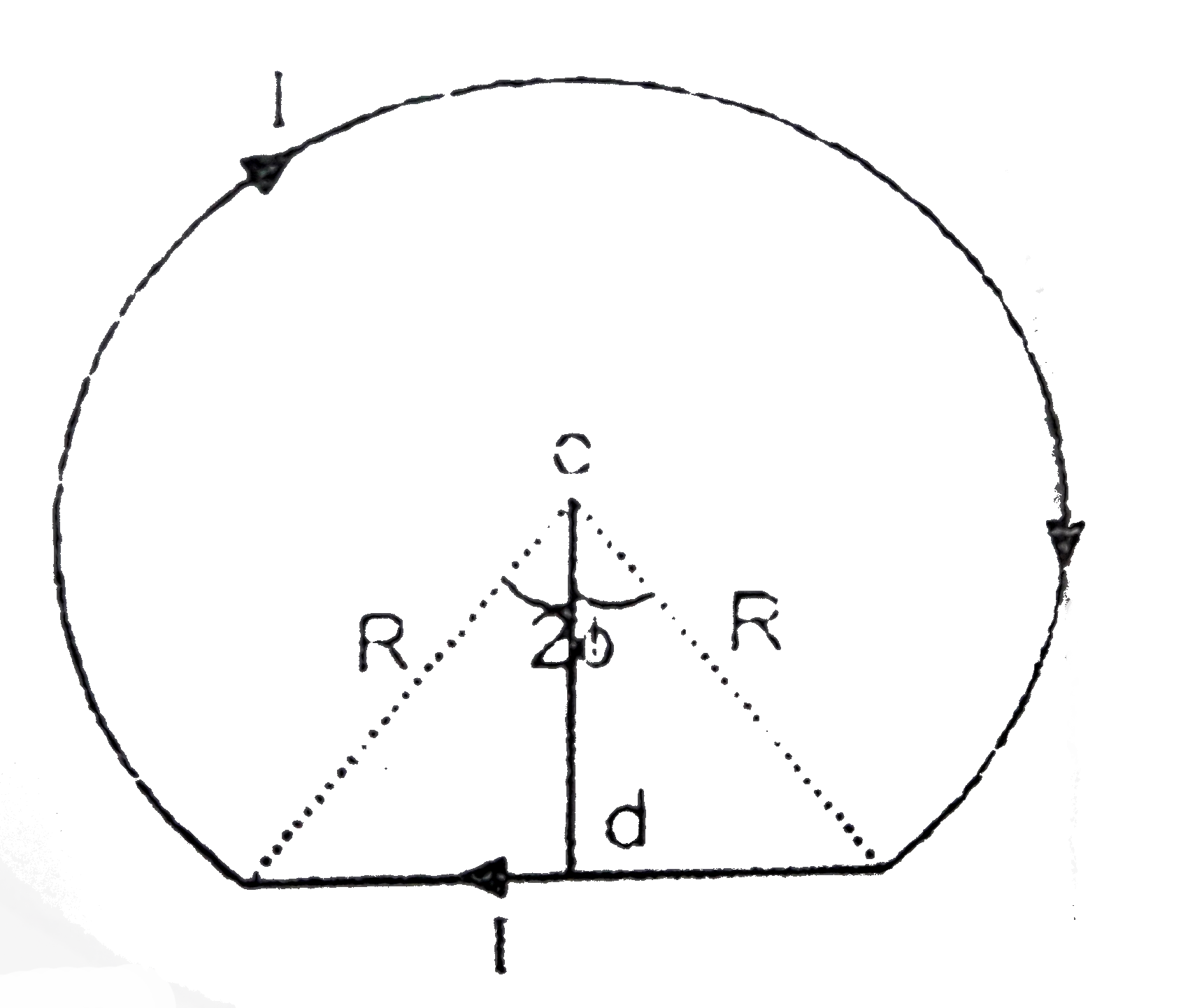
A current I=5.0A A flows along a thin wire shaped as shwon in Fig. The radius of a curved part of the wire is equal to R=120mm, the angle 2φ=90∘. Find the magentic induction of the field at the point O.
View SolutionThe magnetic induction of the field at the point O of a loop with current I, whose shape is given in figure:
View Solution
Knowledge Check
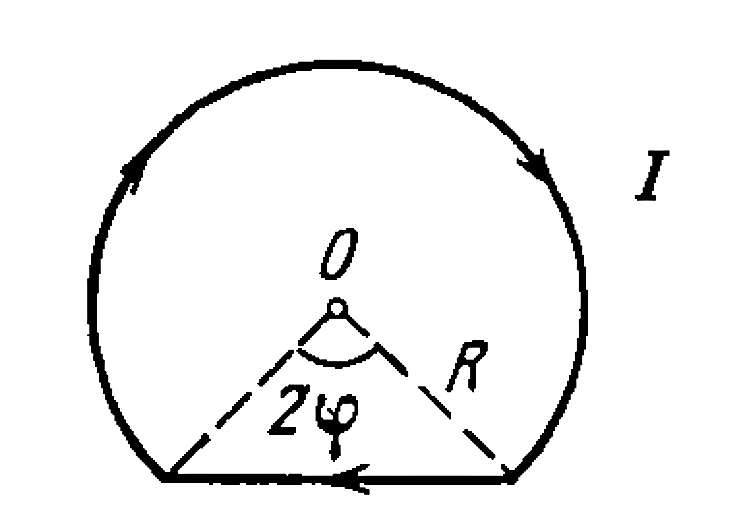
The magnetic field intensity at the point O of a loop with current I, whose shape is illustrated below is
 Aμ0i4π[3π2a+√2b]Bμ0i4π2[2a+b]Cμ0i2π[1a+1b]Dμ0i4π[1a+1b]
Aμ0i4π[3π2a+√2b]Bμ0i4π2[2a+b]Cμ0i2π[1a+1b]Dμ0i4π[1a+1b]A current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
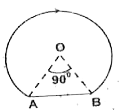 Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)
Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)
Find the magnetic induction of the field at the point O of a loop with current I, whose shape is ilustrated
(a) in Fig. the radil a and b as welll as the angle φ are known,
(b) In Fig , the radius a and the side b are known.
View SolutionThe magnetic field intensity at the point O of a loop with current I, whose shape is illustrated below is

View SolutionA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:

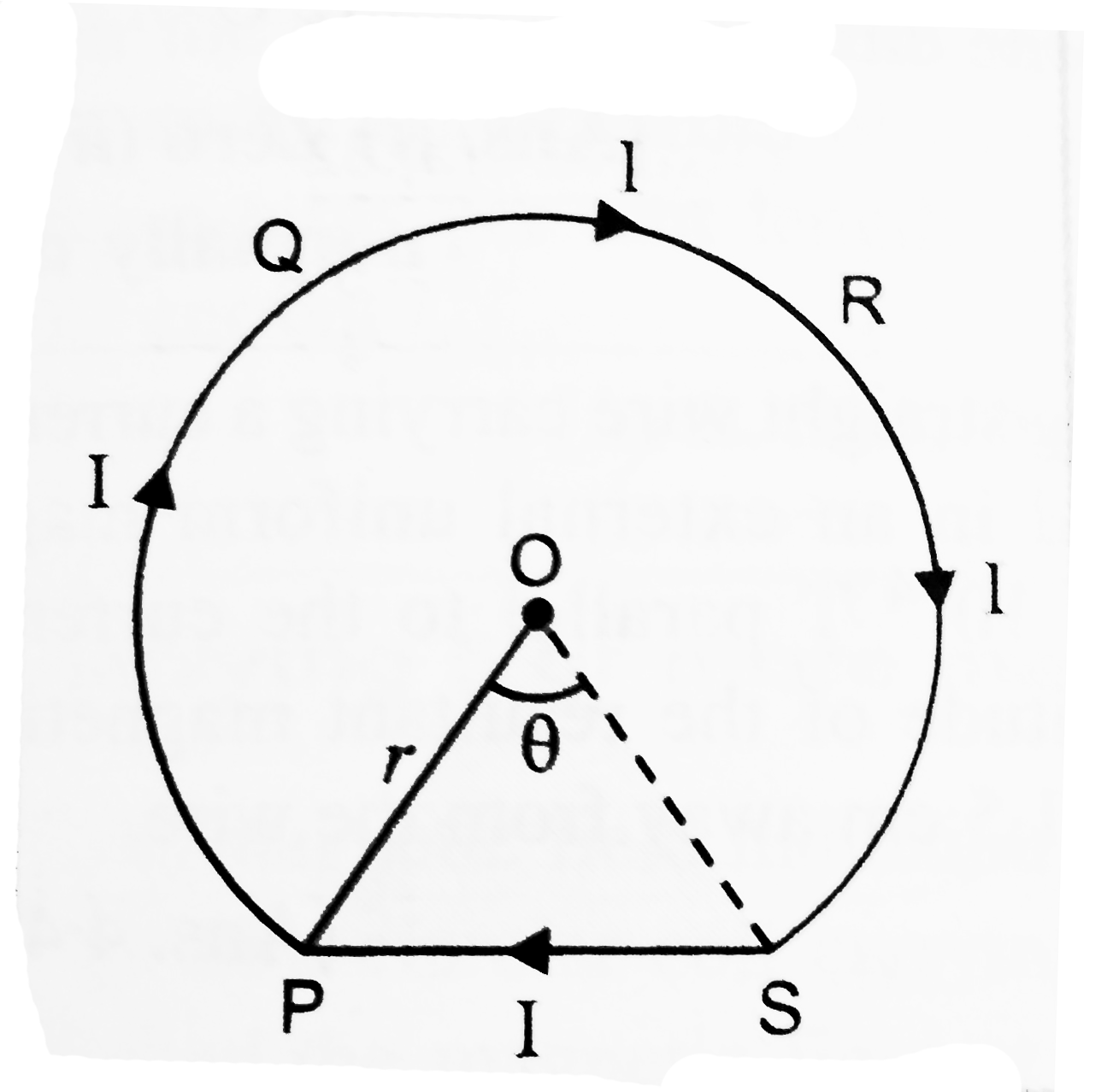
View SolutionA current I(=4A) flows along a thin wire PQRS shaped as shown in figure. The radius of the curved part of the wire is 10⋅0cm. The angle θ=90∘. Find the magnitude of the total magnetic field at the point O.
View SolutionThe magnetic induction of the field at the point O of a loop with current O of a loop with current I, whose shape is illustrated below is-
View SolutionFind the magnetic induction at the point O due to the loop current I in the two cases given below. The shape of the loop are illustrated as
(a) In figure-4.17 (a), the radii A and b, as well as the angle ϕ are known.

(b) In figure 4.17 (b), the radius a and the side b are known.

View Solution
