The magnetic field at the origin due to a current element I(→dl) placed at a positon →r is
μ0i4πd→l×→rr3
−μ0i4πr×→rr3
μ0i4πd→l×→rr3
−μ0i4πd→l×→rr1
The correct Answer is:C, D
Step by step video, text & image solution for The magnetic field at the origin due to a current element I(vec dl ) placed at a positon vec r is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION-15videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION-23videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-226videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
- BOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Find the magnitude of the magnetic field at the origin O due to very long conductor carrying current I of the shape as shown in figure.
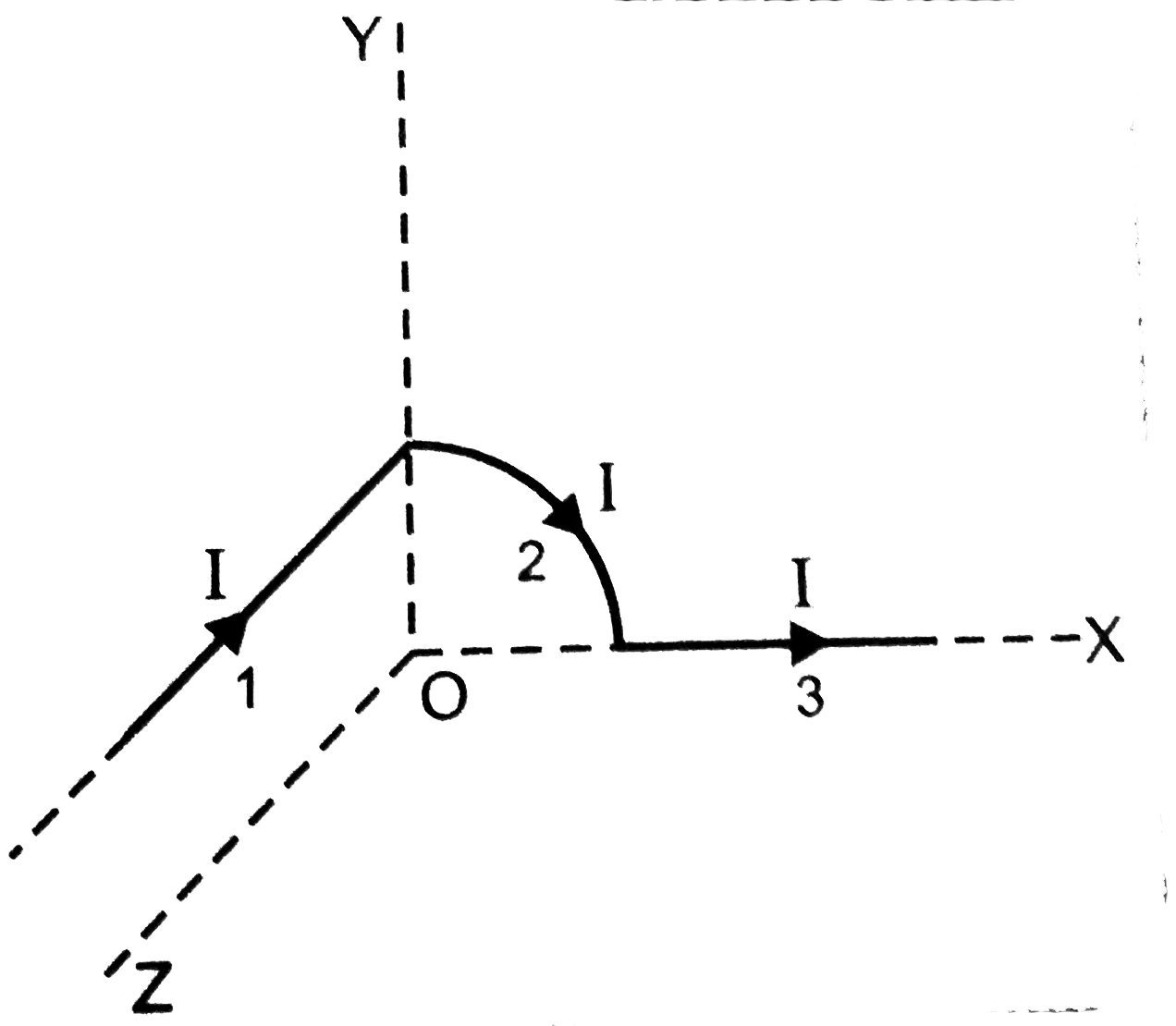 View Solution
View SolutionFind the magnetic field at the ccentre of a current carrying conductor bent in the form of an arc subtending angle θ at its centre. Radius of the arc is R
Strategy: Let the arc lie in x-y plane with its centre at the origin. Consider a small current element i→dl as shown. The field due to this element at the centre can be obtained by Biot-Savart lawView Solution
Knowledge Check
- Question 1 - Select One
The magnetic field at the origin due to a current element I→dl placed at position r is
(i) (μ0i4π)(d→l×→rr3)
−(μ0i4π)(d→l×→rr3)
(iii) (μ0i4π)(→r×d→lr3)
−(μ0i4π)(→r×d→lr3)A(i),(ii)B(ii),(iii)C(i),(ii)D(iii),(iv) - Question 2 - Select One
The magnetic field at the origin due to the current flowing in the wire is
 A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk)
A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk) - Question 3 - Select One
The magnetic field −→dB due to a small current element →dl carrying a current I at a distance →r is given as
A−→dB=μ04πI⎡⎣−→dI×→rr⎤⎦B−→dB=μ04πI2⎡⎣→dl×→rr⎤⎦C−→dB=μ04πI2⎡⎣→dl×→rr2⎤⎦D−→dB=μ04πI⎡⎣→dl×→rr3⎤⎦
What is the magnetic field ∣∣→B∣∣ at the point P due to a current carrying wire of length AB (having a current of 2A) shown in figure ?
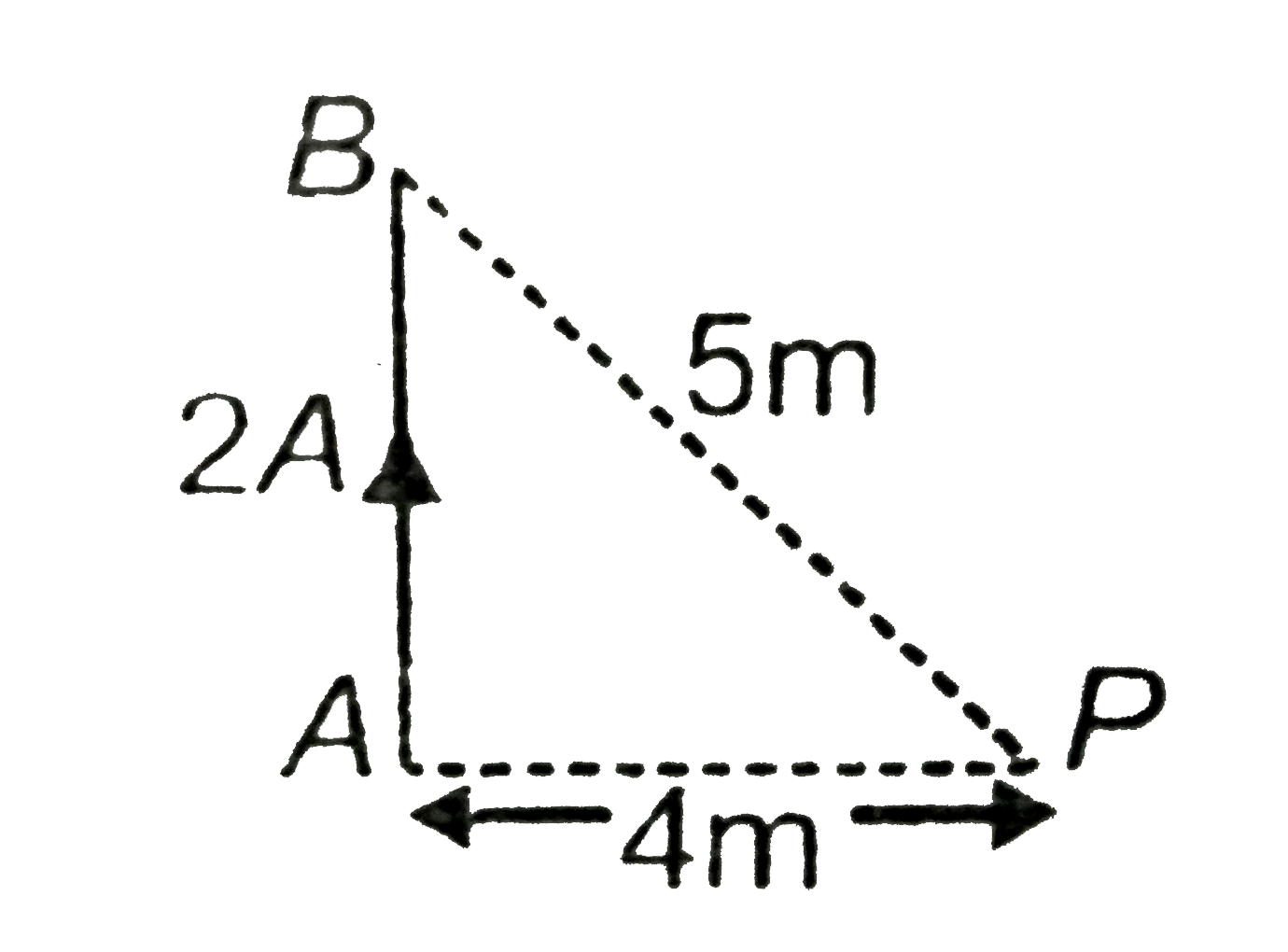 View Solution
View SolutionState the Biot-Savart's law for the magnetic field due to a current carrying element. Use this law to obtain a formula for magnetic field at the centre of a circular loop of radius R carrying a steady current I, sketch the magnetic field lines for a current loop clearly indicating the direction of the field.
View Solution(a) State Bio-Savart's law in vector form expressing the magnetic field due to an element →dl carrying current I at a distance r from the element.
(b) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius 'R' carrying a steady current I. Draw the field lines due to the current loop.View SolutionThe magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
View SolutionThe magnetic field d→B due to a small current element d→l at a distance →r and element carrying current i is,
View Solution

