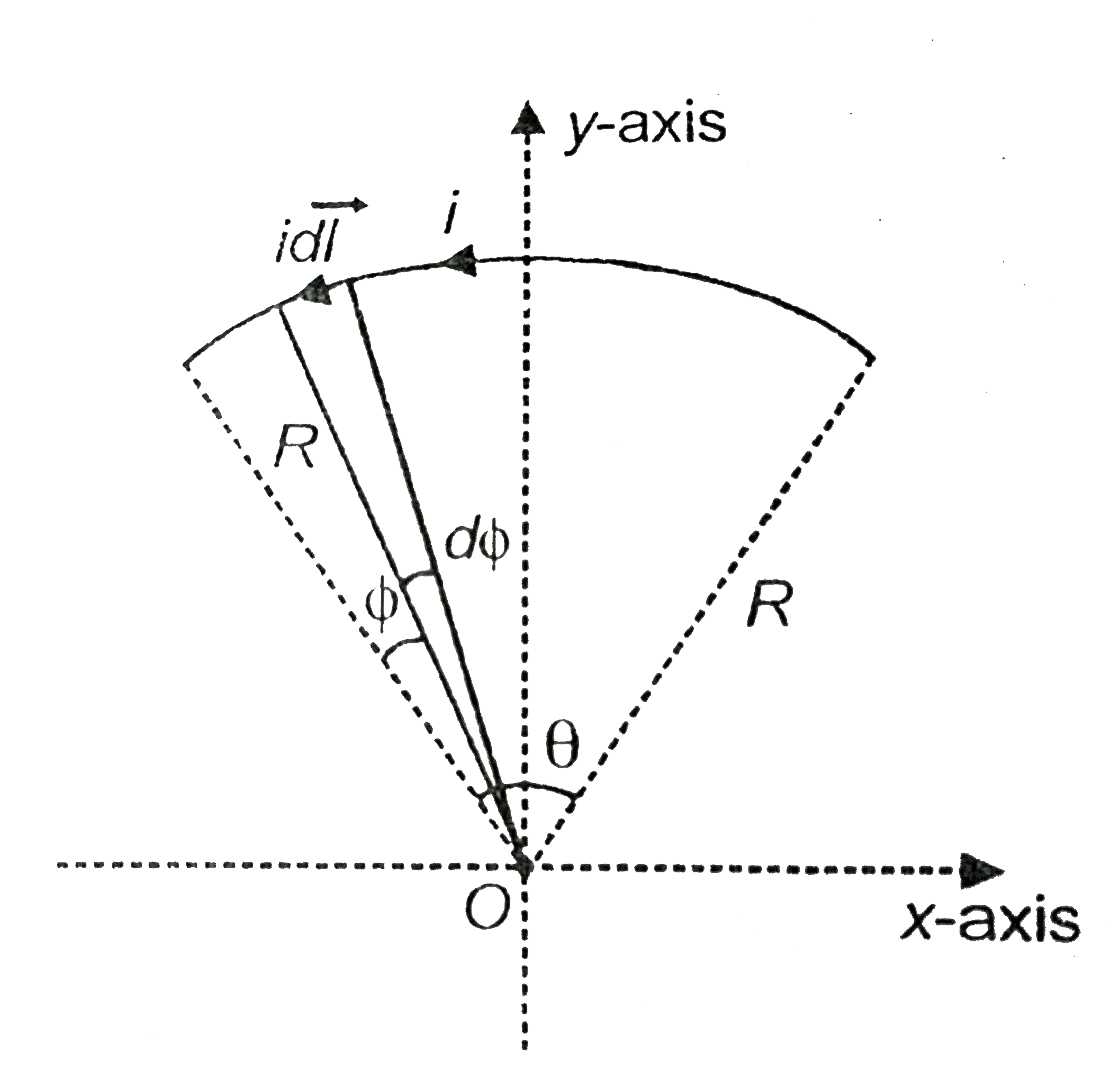
Find the magnetic field at the ccentre of a current carrying conductor bent in the form of an arc subtending angle θ at its centre. Radius of the arc is R
Strategy: Let the arc lie in x-y plane with its centre at the origin. Consider a small current element i→dl as shown. The field due to this element at the centre can be obtained by Biot-Savart law
dB=μ04πsin90∘R2 (∵i→dlandR are perpendicular)
Now dl=Rdϕ
∴dB=μ04πiRdϕR2⇒dB=μ04πiRdϕ
The direction of field is outward perpendicular to plane of paper.
Total magnetic field
B=∫dB∴B=μ0i4πR∫00dϕ=μ0i4πR[ϕ]θ0
∴B=μ0i4πRθ
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration12videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself27videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the magnetic field at the centre of arc in the figure below?
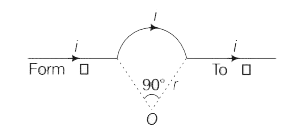 Aμ04π⋅2ir[√2+π]Bμ04π⋅2ir[√2+π4]Cμ04π⋅ir[√2+π]Dμ04π⋅ir[√2+π4]
Aμ04π⋅2ir[√2+π]Bμ04π⋅2ir[√2+π4]Cμ04π⋅ir[√2+π]Dμ04π⋅ir[√2+π4] - Question 2 - Select One
The magnetic field at centre O of the arc in Fig.
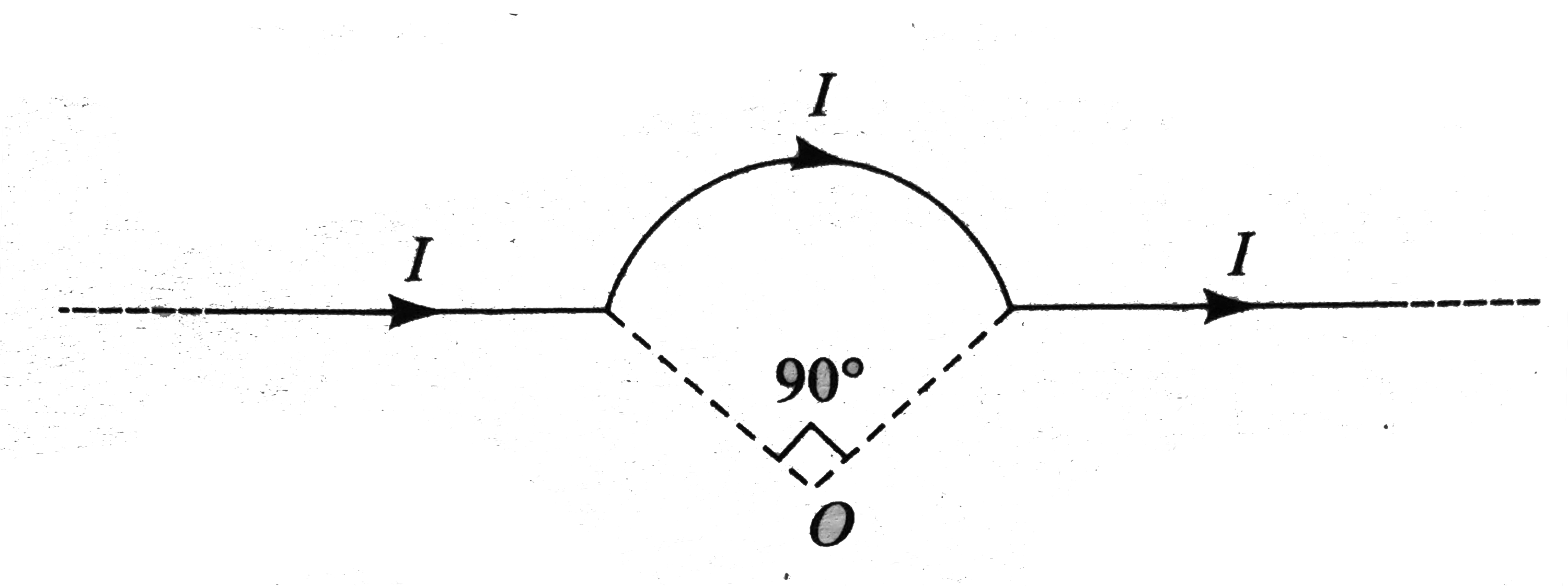 Aμ0I4π×r[√2+π]BμI2πr[π4+(√2−1)]Cμ04π×Ir[(√2−π)]DμI4π×Ir[√2+π4]
Aμ0I4π×r[√2+π]BμI2πr[π4+(√2−1)]Cμ04π×Ir[(√2−π)]DμI4π×Ir[√2+π4] - Question 3 - Select One
In a circle of radius 21 cm, an arc subtends an angle of 72 at the centre. The length of the arc is
A21.6 cmB26.4 cmC13.2 cmD19.8 cm
A piece of wire 20 cm long is bent into the from of an arc of a circle, subtending an angle of 60∘ at its centre. Find the radius of the circle.
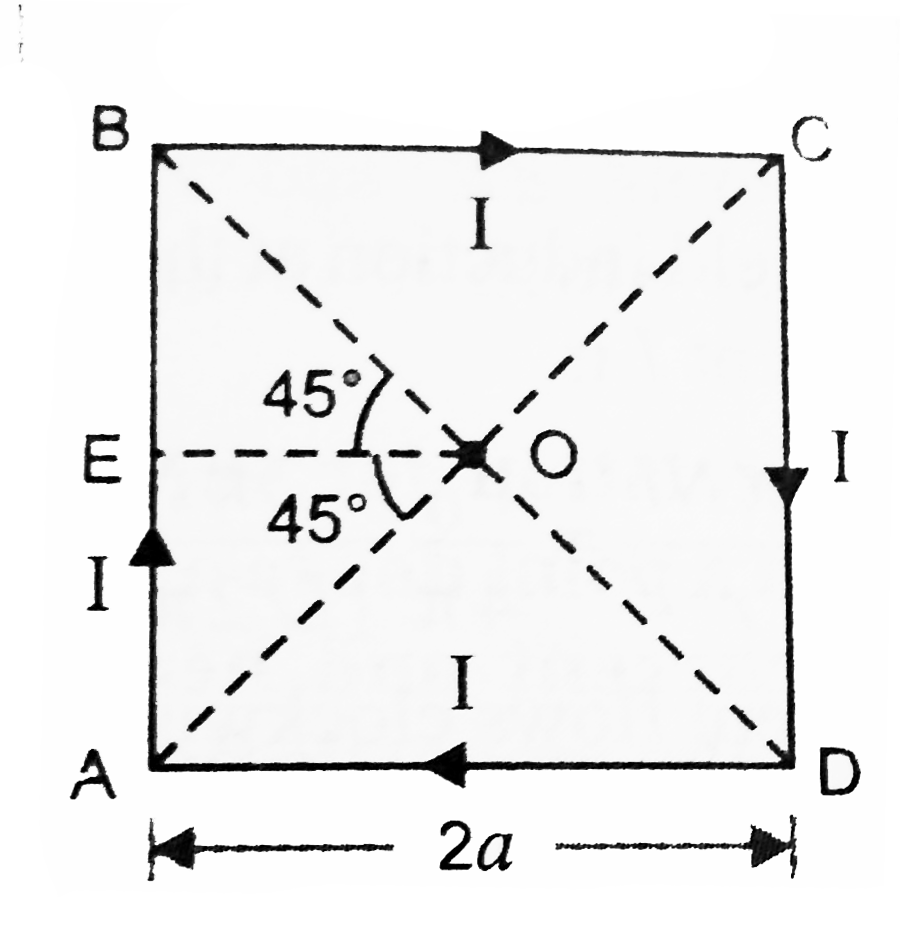
View SolutionFind the experssion for the magnetic field at the centre O of a coil bent in the form of a square of side 2a, carrying current I, figure.
 View Solution
View SolutionThe magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
View SolutionFind an expression for the magnetic field induction at the centre of a coil bent in the form of a square of side 2a, carrying current I, figure
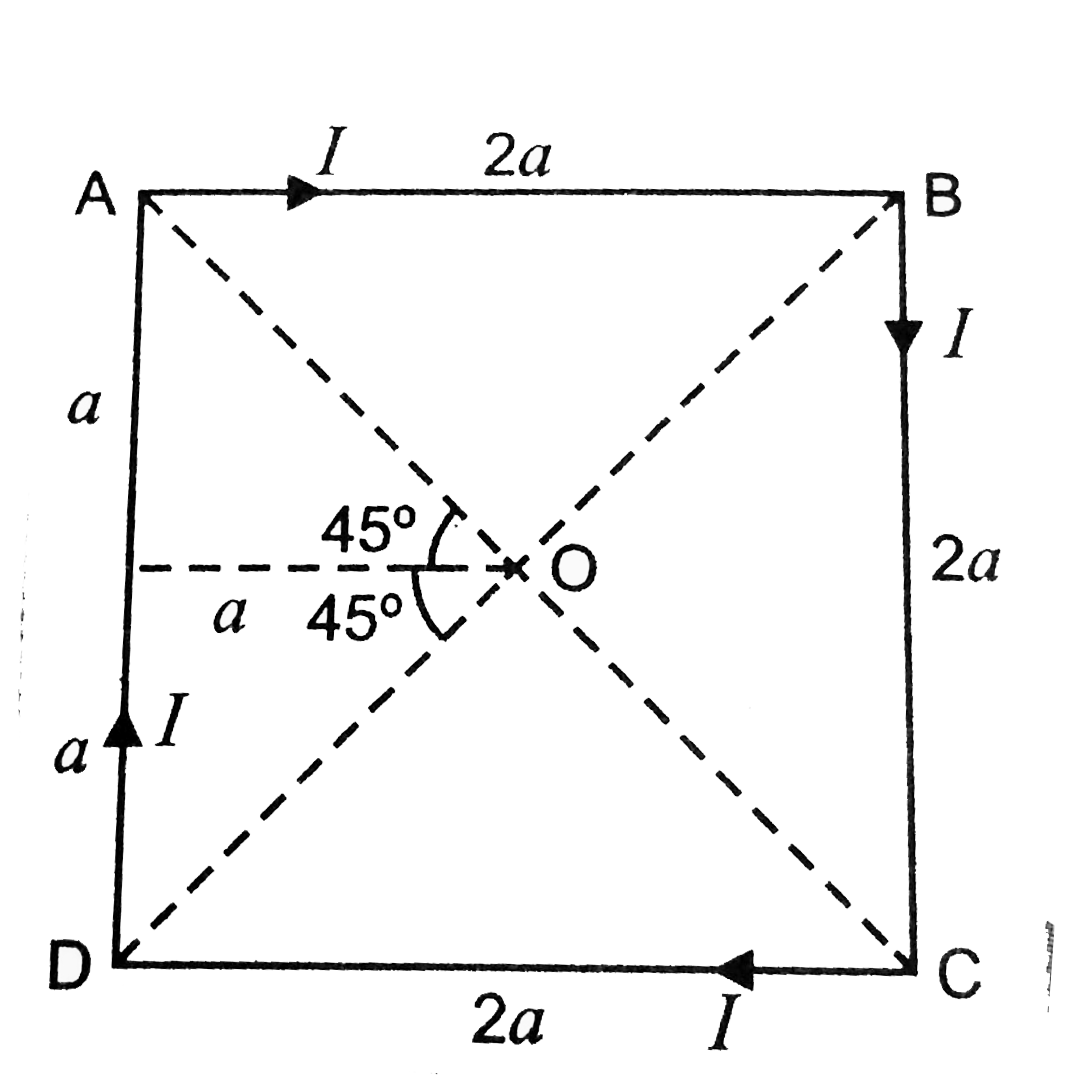 View Solution
View SolutionThe magnetic field at the centre of current carrying coil is B0. If its radius is reduced to half keeping current the same, then magnetic field at its centre become
View Solution

