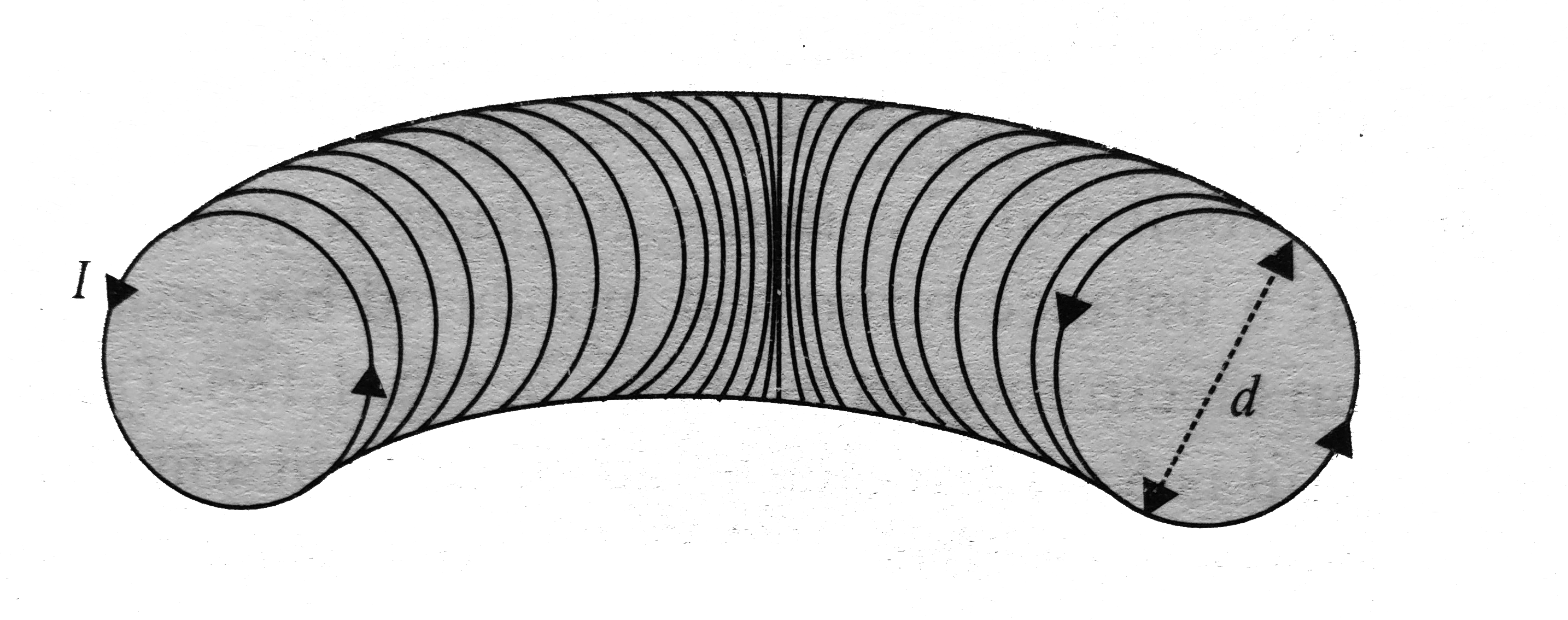
Calculate the magnetic moment of a thin wire with a current I=0.8A, wound tightly on half a toroid (figure).the diameter of the cross-section of the tore is equal to d=5.0cm,the number of turns is N=500.

The correct Answer is:12A.m2
M=π∫θ=0dMsinθ
=π∫θ=0(dN).i.A.sinθ=π∫0Nπ⊥(pd24)sinθdθ
M=12N.i.d2⇒M=12(Ampm2)

Topper's Solved these Questions
Similar Questions
Calculating the magnetic moment ( in Am2) of a thin wire with a current I=8A, wound tightly on a half a tore (see figure). The diameter of the cross section of the tore is equal to d=5cm, and the number of turns is N=500.
View SolutionAn iron tor suports N=500 turns. Find the magnetic field energy if a current I=2.0A preoduces a magnetic flux across the tore's cross-section equal to Φ=1.0mWb.
View Solution(a) Find magnetic field inside a long solenoid, carrying current (1/π) A and having number of turns per unit length 10. Also calculate magnetic field at ends.
(b) A long solenoid is fabricated by closely winding a wire of diameter 10mm over a cylinderical non-magnetic frame so that the successive turns nearly touch each other. Find magnetic field at the centre and ends of solenoid if it carriers a current (4/π) A?
(c) A single-layer coil (solenoid) has length l and cross-section radius R. The number of turns per unit length is equal to n. Find the magnetic induction at the centre of the coil when a current i flows through it.
(d) A solenoid of length 0.4m and diameter 0.6m consists of a single layer of 1000 turns of the fine wire carrying a current of 5mA. Calculate the magnetic field on the axis at the middle and at the ends of the solenoid.
View SolutionA thin ring made of magnetic has a mean diameter d=30cm and supports a winding of N=800 turns. The cross-sectional area of the ring is equal to S=5.0cm2. The ring has a cross-cut of width b=2.0mm. When the winding carries a certain current, the permeability of the magnectic equals μ=1400. Neglectign the disipation of magnetic flux at the gap edges, find:
(a) the ratio of magnetic energies in the gap and in the magnetic,
the inductance of the system, do it two ways: using the flux and using the energy of the field.
View SolutionA wire carrying current of 5 A is wound on a toroid in 4,000 turns, Calculate the magnetic field inside the core of toroid and outside the toroid if its inner radius is 15 cm and the outer radius is 18 cm.
View SolutionIn the problem 1, a coil of 500 turns is wound closely on the toroid. Calculate the induced emf in the coil if the current in toroid is 5 A and it reverses its direction in 0.3 s.
View SolutionA solenoid of length 1⋅0m and 3⋅0cm diameter has five layers of windings of 850 turns each hand carries a current of 5 ampere. What is the magnetic field at the centre of the solenoid? Also calculate the magnetic flux for a cross-section of the solenoid at the centre of the solenoid.
View SolutionA thin wire is wound very tightly in one layer on the surface of a sphere of paramagnetic material (μr≈1). The planes of all the turns can be assumed to be perpendicular to the same diameter of the sphere. The turns over the entire surface of the sphere. The radius of the sphere is R, the total number of turns is N, and the current in the winding is I. Find the magnetic induction at the centre of the sphere. (Given μ0NI=20R)
View SolutionFigure-4.78 shows a toroidal solenoid whose cross-section is rectangular in shape. Find the magnetic flux through this cross-section if the current through the toroidal winding is I, total number of turns in winding is N, the inside and outside radii of the toroid are a and b respectively and the height of toroid is equal to h.

View Solution(a) Calculate the self-inductance of a solenoid that is tightly wound with wire of diameter 0.10cm, has a cross-sectional area 0.90cm2 and is 40cm long
(b) If the current through the solenoid decreases uniformly from 10 A to 0A in 0.10s, what is the emf induced between the ends of the solenoid?
View Solution
