A current of 10A flows around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists oif eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
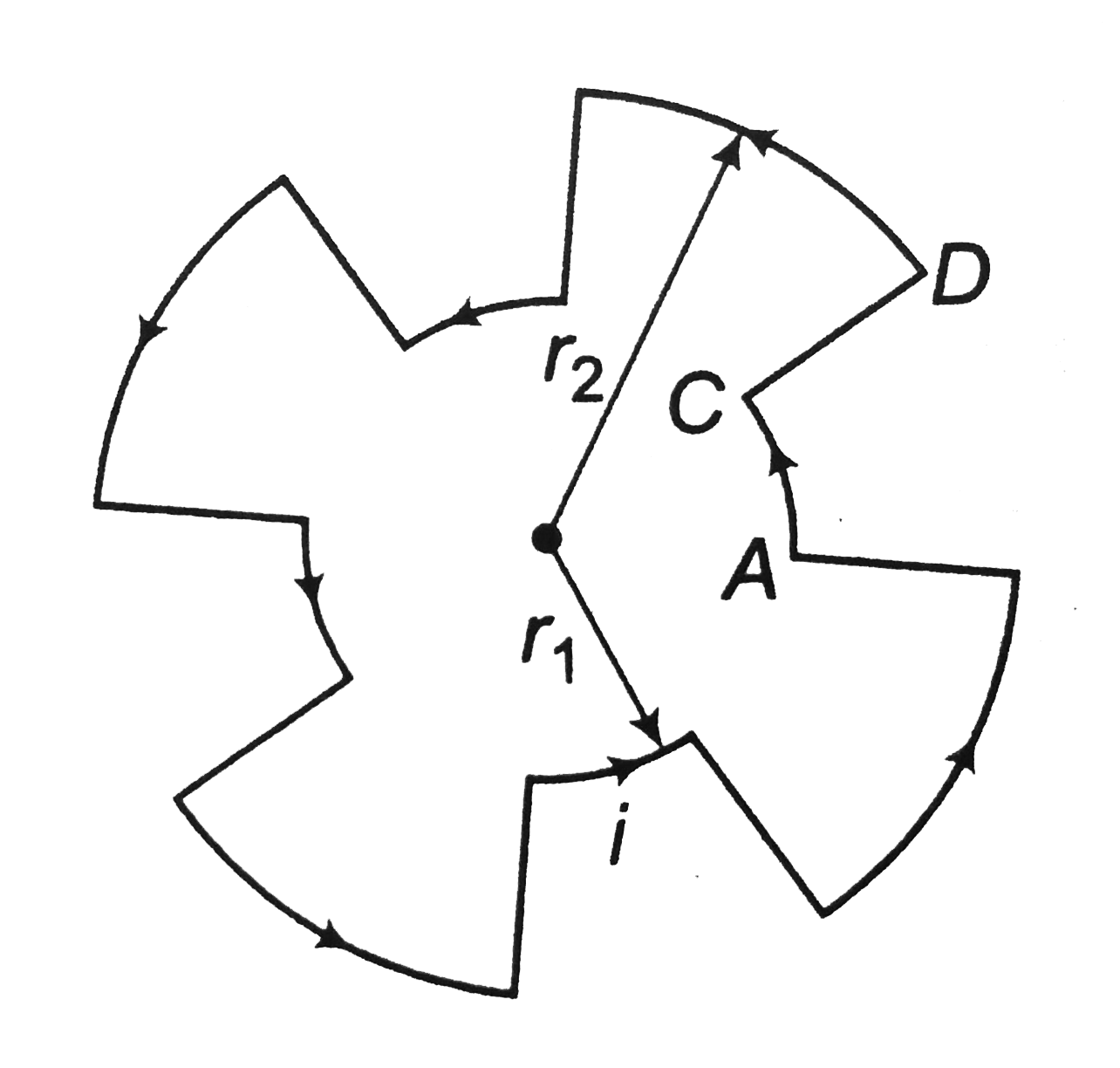
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carryin as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centre due to the current in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
The correct Answer is:(i)Bc=5π×10−424T
(ii)F on central wire =0 ,
FAC=0;FCD=2×10−5In(32)
(a)Giveni=10A,r1=0.08m and r2=0.12m Straight portions i.e. CD etc. will produce zero magnetic field at the centre.Rest eight arcs will produce the magnetic field at the centre in the same direction i.e. perpendicular to the paper putwards to vertically upwards and its magnitude is B=Binner arcs+Bouter arcs
=12{μ0i2r1}+12{μ0i2r2}
={μ0i4π(πi)(r1+r2r1r2)
Substituting the values, we have
B=(10−7)(3.14)(10)(0.08+0.12)(0.08+0.12)Tesla
B=6.54×10−5T(Vertically upward and outward normal to the paper)
Force on AC
(b)Force on circular portions of the circuit i.e. AC etc. due to the wire at the centre will be zero because magnetic field due to the central wire at these arcs will be tangential (θ=180∘) as shown.
Force on CD
Current in central wire is also i=10A
Magnetic field at P due to central wire,
B=μ02πix
∴ Magnetic force on elecent dx due to this magnetic field
dF=(i)(μ02πix).dx=μ02πi2dxx
(F=i/Bsin90∘)
Therefore, net force on CD is
F=x=f2∫x=f1dF=μ0i22π−0.12∫0.08dxx=μ02πi2ln(32)
Substituting the values ,F=(2×10−7)(10)2ln(1.5)
or F=8.1×10−6N (inwards)
Force on wire at the centre Net magnetic field at the centre due to the circuit is in vertical direction and current in the wire in centre is also in vertical direction.Therefore,net force on the wire at the centre will be zero. (θ=180∘).Hence
(i)Force acting on the wire at the centre is zero.
(ii)Force on arc AC=0.
(iii)Force on segment CD is 8.1×10−6N(inwards).


Topper's Solved these Questions
Similar Questions
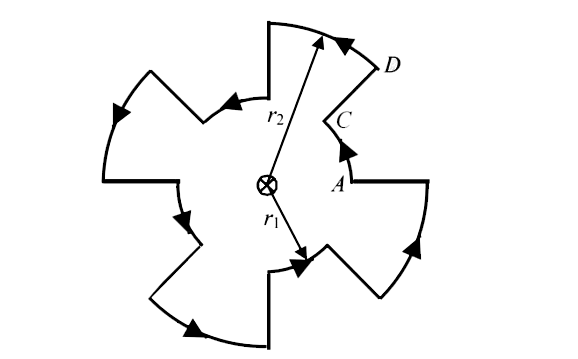
A current of 10A flows around a closed path in a circuit which is int eh horizontal plne as shown in the figure. The circuit consists oif eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.

a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carryin as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centredue to the curren in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?View SolutionA current of 10A flows around a closed path in a circuit which is in horizontal plane as shown in the figure . The circuit consists of eight alternating arcs of radiir1=0.08mandr1=0.12m.Eacharc⊂tendsthesameathecenter.<br>(a)F∈dthemag≠tixcfield∏ucedbythis∘uitatthecenter.<br>(b)An∈f∈itelylongstraightwirecarry∈gacurrentof10 Aispassingthroughthecenteroftheabove∘uitverticallywiththedirectionofthecurrentbe∈g∫othepla≠ofthe∘uit.Wˆistheforceact∈gonthearcACandthestraightsegment CD due to the current at the center?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A current I flows around a closed path in the horizontal plane of circle as shown in the figure The path consists of eight arcs with alternating radii r and 2r . Each segment of arc subtends equal angle at the common centre P The magnetic field produced by current path at point P is
 .A38μ0Ir , perpendicular to the plane of the paper and directed inward .B38μ0Ir , perpendicular to the plane of the paper and directed outward .C38μ0Ir , perpendicular to the plane of the paper and directed inward .D38μ0Ir , perpendicular to the plane of the paper and directed outward .
.A38μ0Ir , perpendicular to the plane of the paper and directed inward .B38μ0Ir , perpendicular to the plane of the paper and directed outward .C38μ0Ir , perpendicular to the plane of the paper and directed inward .D38μ0Ir , perpendicular to the plane of the paper and directed outward . - Question 2 - Select One
In the circuit shown in figure current in the circuit is
 A1.27AB2.23AC4.26AD4 A
A1.27AB2.23AC4.26AD4 A - Question 3 - Select One
The magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
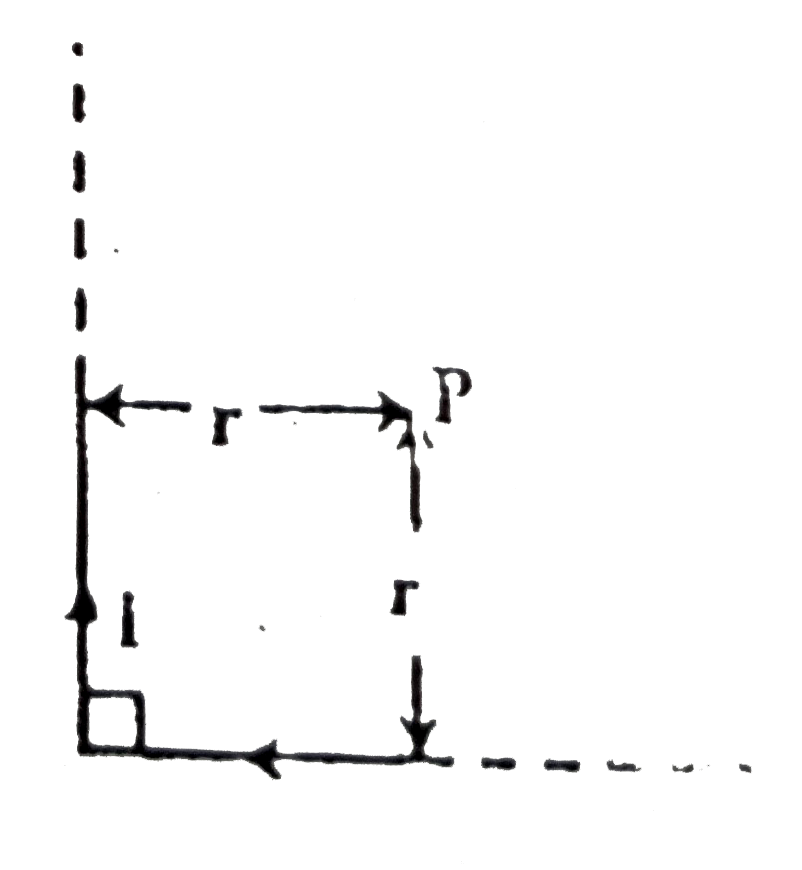 Aμ0Bμ0i/2√2rC(μ0i/√2πr)Dμ0i4πr[2+√2]
Aμ0Bμ0i/2√2rC(μ0i/√2πr)Dμ0i4πr[2+√2]
Switch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png) View Solution
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.
 View Solution
View SolutionAn L-R circuit has a cell of e.m.f. E , which is switched on at time t = 0. The current in the circuit after a long time will be
View SolutionAn arc of a circle of radius R subtends an angle π2 at the centre. It carriers a current i. The magnetic field at the centre will be
View Solution

