ABC is an isosceles triangle with AB=AC and D is a point on ABC BC such that AD⊥BC (see figure ). To prove that ∠BAD=∠CAD a student proceeded as follows
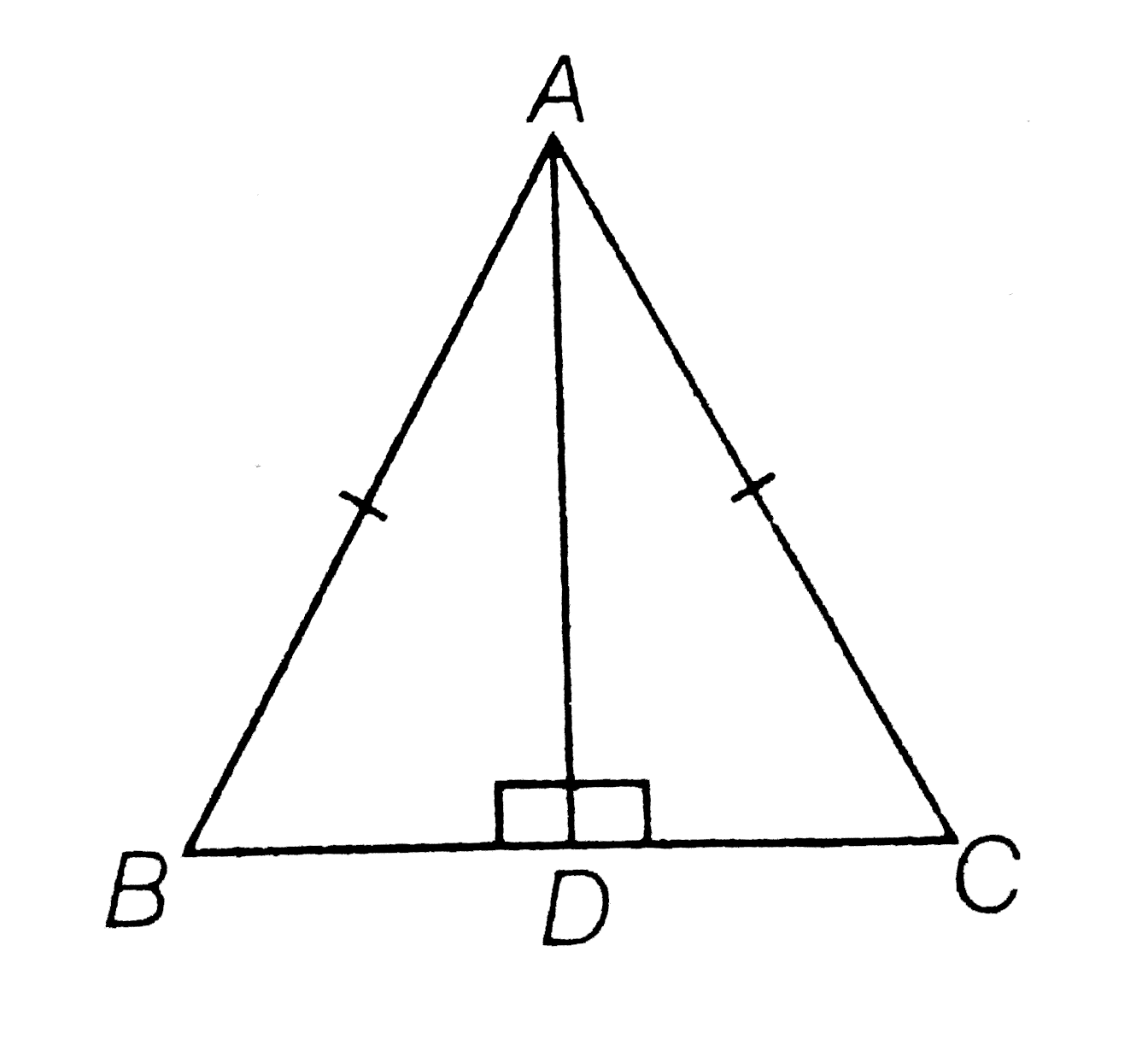
InΔABDandΔACD,we have
AB=AC [ Given]
∠B=∠C [∵ AB=AC ]
and ∠ADB=∠ADC
Therefore ΔABD≅ΔACD [by AAS congruence rule]
So , ∠BAD=∠CAD [byCPCT]
What is the defect in the above argument ?
In ΔABC, AB=AC [given]
⇒ ∠ACB=∠ABC [angles opposite to equal sides are equal ]
in ΔABDandΔACD,
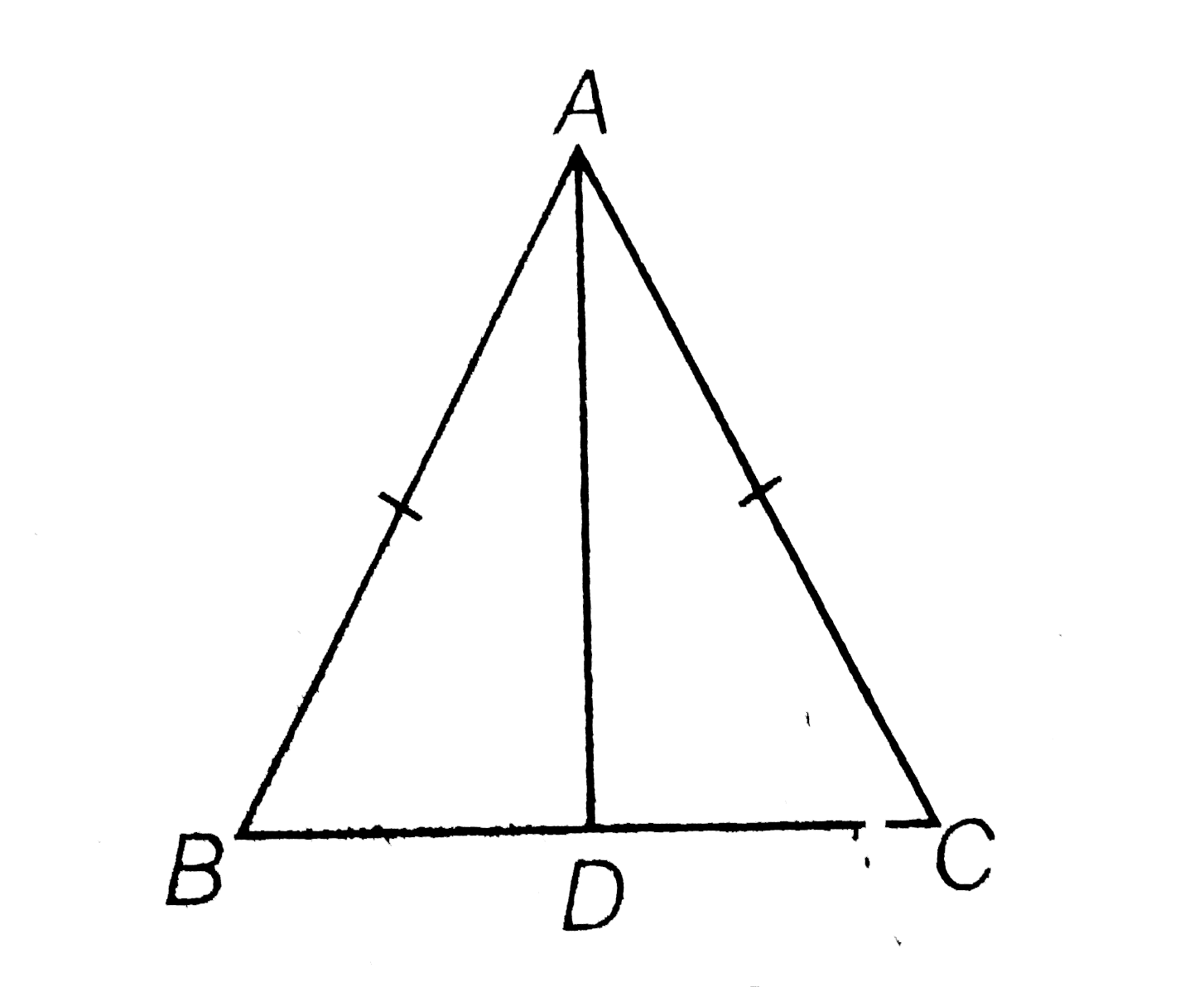
AB=BC
∠ABD=∠ACD [given ]
∠ABD=∠ACD [proved above ]
∠ADB=∠ADC [each 90∘]
∴ ΔABD≅ΔACD [by AAS ]
So ∠BAD=∠CAD [ by CPCT ]
So the defect in the given argument in that firstly prove ∠ABD=∠ACD Hence ,∠ABD=anl≥ACD is defect ,
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS
11 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
- VOLUME AND SURFACE AREABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS
8 Videos
Similar Questions
ABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn ΔABC,AB=ACandD is a point an side AC such that AD = BD = BC . Show that : ∠ADB=108∘
View SolutionABC is an isosceles triangle with AC = BC. If AB2=2AC2, prove that ABC is a right triangle.
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

ΔADE~ΔACB.
View Solution