A star of mass m revolves in radius R in galaxy in which density varies with distance r as ρ=kr, k=constant. Find the relation between time period and radius R
T×R32 is constant
T×R−12 is constant
T×R72 is constant
T×R is constant
The correct Answer is:B
To solve the problem, we need to find the relationship between the time period T of a star revolving in a galaxy and the radius R of its orbit, given that the density ρ of the galaxy varies with distance r as ρ=kr.
1. Determine the Mass of the Galaxy:
- The density of the galaxy is given as ρ=kr.
- We consider a spherical shell of radius r and thickness dr. The volume dV of this shell is:
dV=4πr2dr
- The mass dm of this shell can be expressed as:
dm=ρ⋅dV=kr⋅4πr2dr=4πkrdr
- To find the total mass M of the galaxy up to radius R, we integrate dm from 0 to R:
M=∫R04πkrdr=4πk(r22)R0=4πk⋅R22=2πkR2
2. Apply Newton's Law of Gravitation:
- The gravitational force F acting on the star of mass m due to the mass M of the galaxy is given by:
F=GMmR2
- Substituting the expression for M:
F=G(2πkR2)mR2=2πGkm
3. Centripetal Force Requirement:
- The centripetal force required to keep the star moving in a circular orbit is given by:
Fc=mv2R
- Setting the gravitational force equal to the centripetal force:
2πGkm=mv2R
- Canceling m from both sides (assuming m≠0):
2πGk=v2R
- Rearranging gives us:
v2=2πGkR
4. Relate Velocity to Time Period:
- The time period T of the star's orbit is given by the circumference of the circle divided by the velocity:
T=2πRv
- Substituting v from the previous step:
T=2πR√2πGkR=2πR√2πGk√R=2π√R√2πGk
5. Final Relation:
- Thus, we can express the relationship between the time period T and the radius R:
T∝√R
- This means that the time period T is proportional to the square root of the radius R.
- The density of the galaxy is given as ρ=kr.
- We consider a spherical shell of radius r and thickness dr. The volume dV of this shell is:
dV=4πr2dr
- The mass dm of this shell can be expressed as:
dm=ρ⋅dV=kr⋅4πr2dr=4πkrdr
- To find the total mass M of the galaxy up to radius R, we integrate dm from 0 to R:
M=∫R04πkrdr=4πk(r22)R0=4πk⋅R22=2πkR2
- The gravitational force F acting on the star of mass m due to the mass M of the galaxy is given by:
F=GMmR2
- Substituting the expression for M:
F=G(2πkR2)mR2=2πGkm
- The centripetal force required to keep the star moving in a circular orbit is given by:
Fc=mv2R
- Setting the gravitational force equal to the centripetal force:
2πGkm=mv2R
- Canceling m from both sides (assuming m≠0):
2πGk=v2R
- Rearranging gives us:
v2=2πGkR
- The time period T of the star's orbit is given by the circumference of the circle divided by the velocity:
T=2πRv
- Substituting v from the previous step:
T=2πR√2πGkR=2πR√2πGk√R=2π√R√2πGk
- Thus, we can express the relationship between the time period T and the radius R:
T∝√R
- This means that the time period T is proportional to the square root of the radius R.
Topper's Solved these Questions
Similar Questions
The earth is a homogeneous sphere of mass M and radius R. There is another spherical planet of mass M and radius R whose density changes with distance r from the centre as p=p0r. (a) Find the ratio of acceleration due to gravity on the surface of the earth and that on the surface of the planet. (b) Find p0.
View SolutionIf the current density in a linear conductor of radius 'a' varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor. Find the magnetic field induction at a point distance r from the axis, when (i) r<a and (ii) r>a.
View Solution
Knowledge Check
- Question 1 - Select One
An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
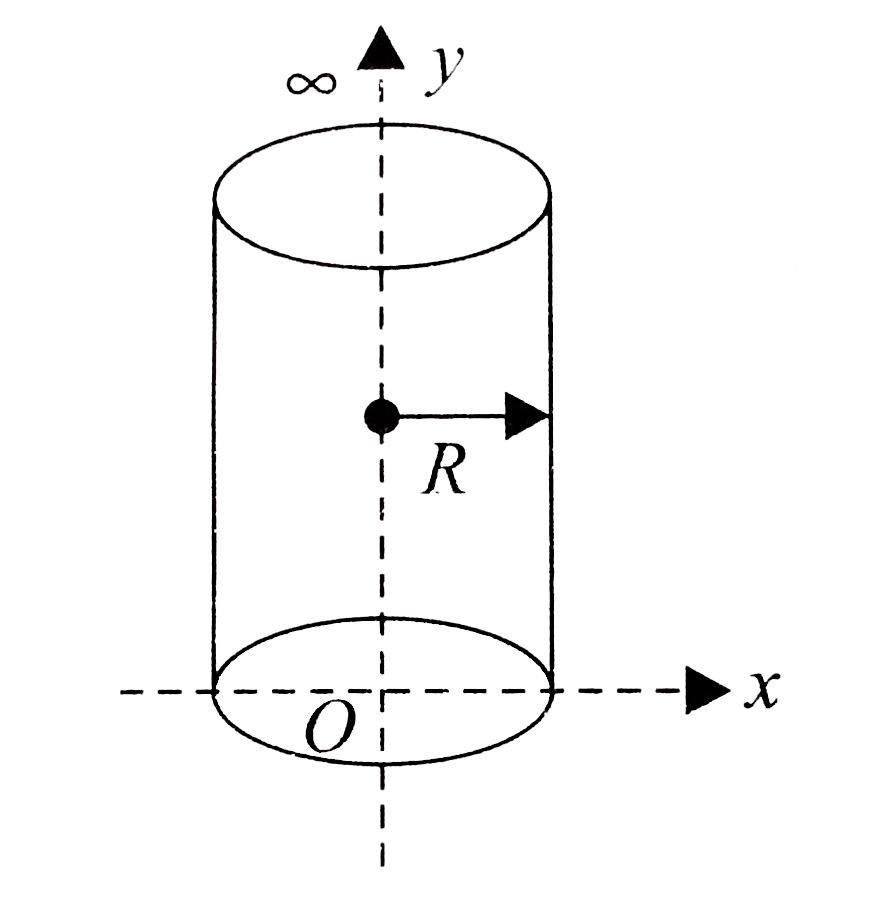
Graph between the magnetic field and radius isA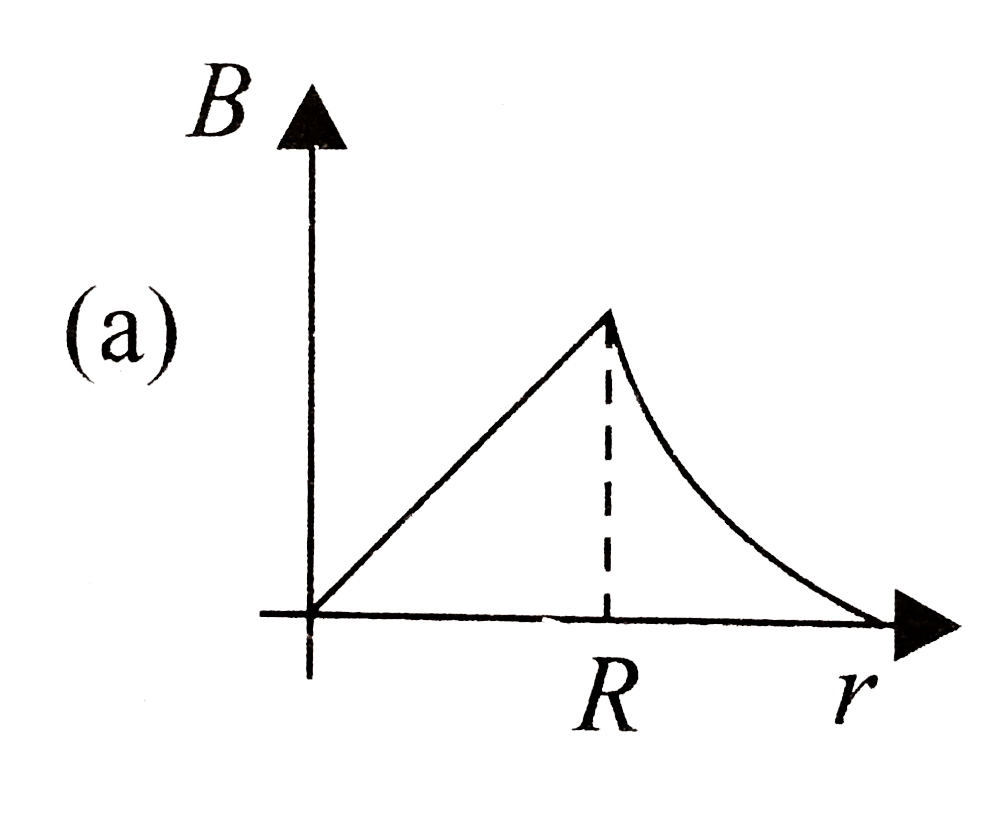 B
B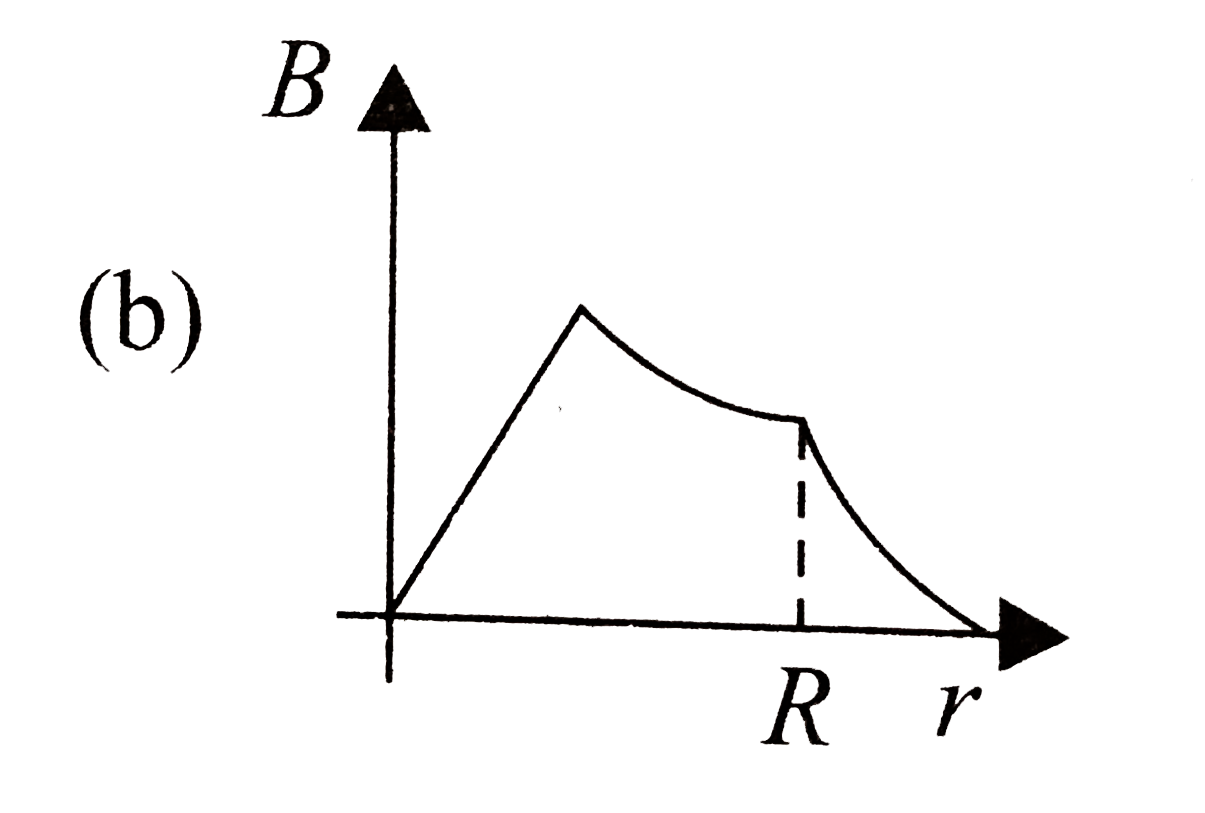 C
C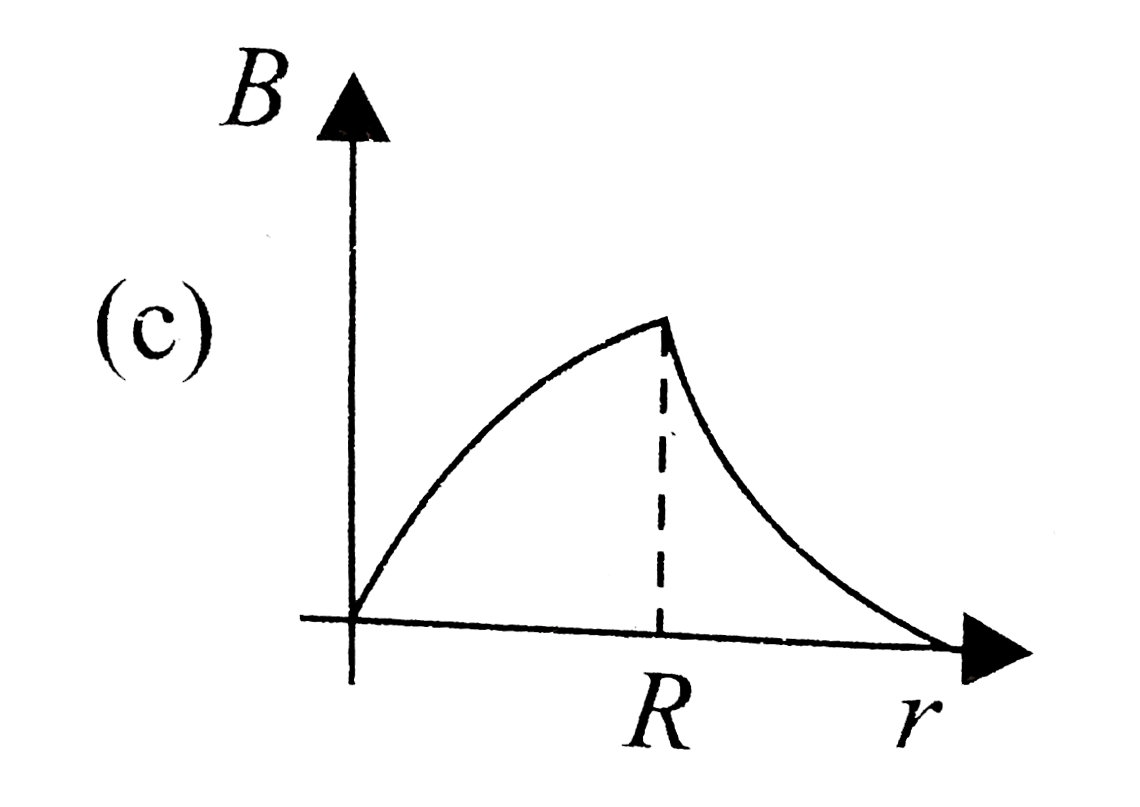 D
D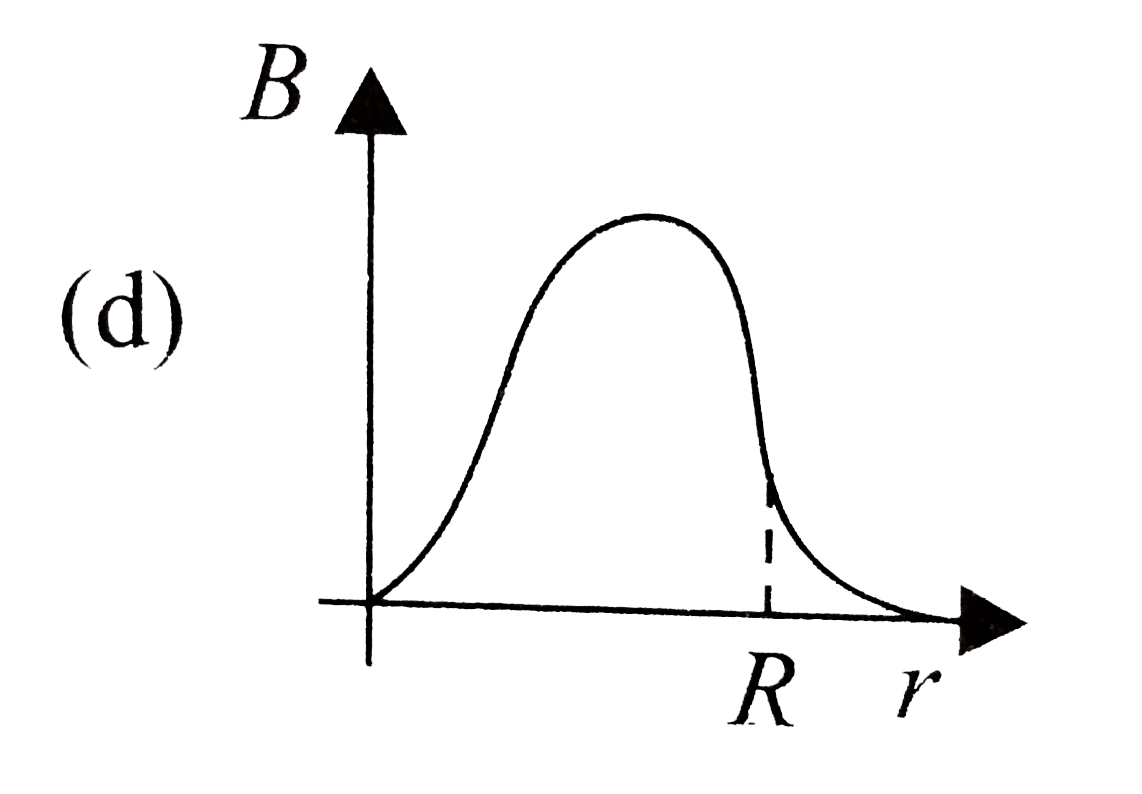
- Question 2 - Select One
The current density in a wire of radius a varies with radial distance r as J=J0r2a, where J0 is a constant. Choose the incorrect statement.
ATotal current passing through the cross-section of the wire isI=πJ0a32BTotal current passing through the cross-section of the wire isI=3πJ0a32CThe field at a distance r gt a is B=μ0J0a34rDThe field at a distance r gt a is B=μ0J0a34a - Question 3 - Select One
If radius of an octahedral void is r and atomic radius of atoms assuming cubical close pacting is R. Then the relation between r and R is
Ar = 2RBr = 1.414 RCr = 0.414 RDr=R√2
A satellite of mass M is moving in a circle of radius R under a centripetal force given by (-K//R^(2)), where k is a constant. Then
View SolutionA particle of mass m is moving in a circular path of constant radius r, such that its centripetal force Fr varies with time t as Fr=K2rt2, where k is a constant. What is the power delivered to the particle by the forces acting on it?
View SolutionA test particle is moving in a circular orbit in the gravitational field produced by a mass density ρ(r)=Kr2. Identify the correct relation between the radius R of the particle’s orbit and its period T:
View SolutionA solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
View SolutionA small planet is is revolving around a very massive star in a circular orbit of radius r with a period of revolution. T is the gravitational force between the planet and the star is proportional to r−5/2 ,then T will be proportional to
View Solution

