Light incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.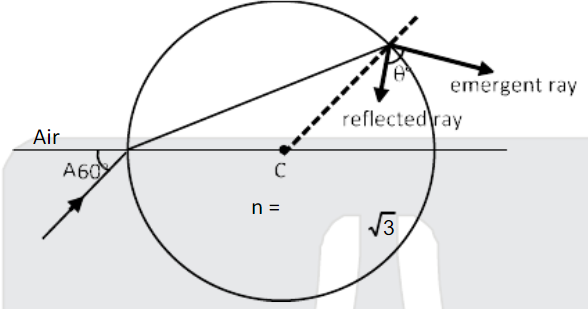 
Step by step video & image solution for Light incidence on a sphere of refractive index sqrt3 placed in a air as shown in Figure. Find the angle (theta)in degree between emergent ray and reflected ray. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
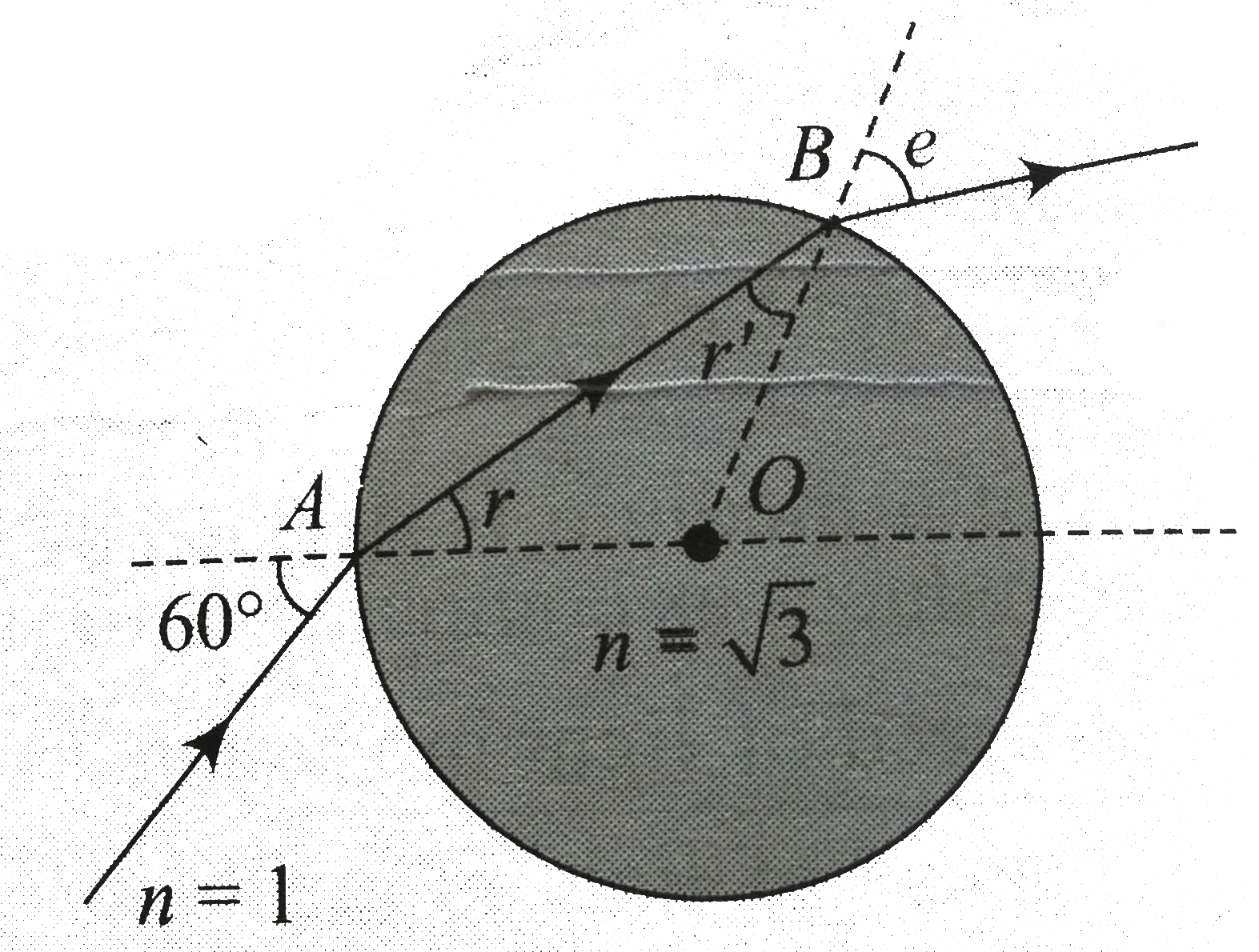
View Solution
A ray is incident on a sphere of refractive index √2 as shown in figure. Angle of refraction of the ray inside sphere is 30∘ if total deviation suffered by the ray is 30x0, then find x.View Solution
Knowledge Check
- Question 1 - Select One
A ray of light enters a spherical drop of water of refractive index p as shown in the figure.
An expression of the angle between incidence ray and emergent ray (angle of deviation) as shown in the figure is
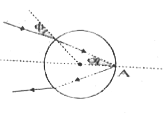A0∘BϕCα−ϕDπ−4α+2ϕ - Question 2 - Select One
A ray of light enters a spherical drop of water of refractive index μ as shown in figure.
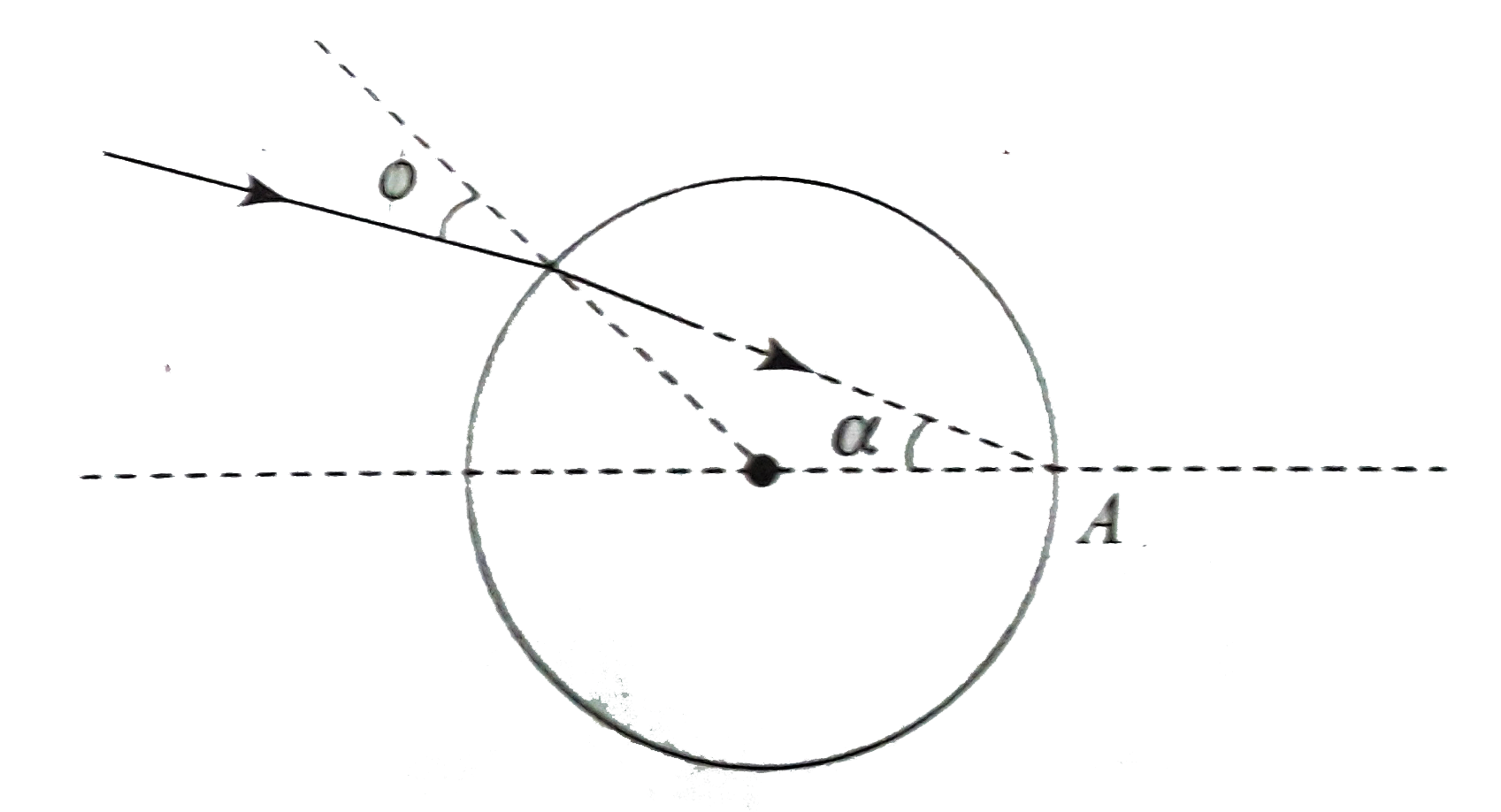
Q. An expression of the angle between incident ray and emergent ray (angle of deviation) as shown in figure.
A0∘BϕCα−ϕDπ−4α+2ϕ - Question 3 - Select One
A ray of light incident on a glass sphere (refractive index √3 ) suffers total internal reflection before emerging out exactly parallel to the incident ray. The angle of incidence was
A75∘B30∘C45∘D60∘
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View SolutionA ray of light strikes a tansparent rectangular slab (of refractive index √2) At an angle of incidence of 45∘. The angle between the reflected and refracted rays is
View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View SolutionA ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle between the reflected and refracted rays is
View Solution