নীচের প্রতিক্ষেত্রে স্পর্শক ও অভিলম্বের সমীকরণ নির্ণয় করো
x23+y23=2 বক্রের ওপর (1,1) বিন্দুতে
Step by step video & image solution for নীচের প্রতিক্ষেত্রে স্পর্শক ও অভিলম্বের সমীকরণ নির্ণয় করো x^frac(2)(3)+y^frac(2)(3)=2 বক্রের ওপর (1, 1) বিন্দুতে by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
সঠিক উত্তরটি নির্বাচন করো
y=f(x)সম্ভত লঞ্জের ওপর(x1,y1) বিন্দুতে অঙ্কিত অভিলম্বের নতি m হলে m =
View Solutionসঠিক উত্তরটি নির্বাচন করো
limx→0e3x−12x -এর মান হবে -
View Solutionx2+y3=1-হলে (x2+y2)এর লঘিষ্ঠ মান নির্ণয় করো।
View Solutionমনে করো xy সমতলে অবস্থিত S একটি বৃত্ত, যা x2+y2 = 4 সমীকরণ দ্বারা সংজ্ঞাত। মনে করো S বৃত্তের ওপর P এমন একটি বিন্দু যার স্থানাঙ্ক দুটি (x স্থানাঙ্ক ও yস্থানাঙ্ক) ধনাত্মক। মনে করো P বিন্দুতে S বৃত্তের স্পর্শক অক্ষদ্বয়কে M ও N বিন্দুতে ছেদ করেছে। তবে MN সরলরেখার মধ্যবিন্দু যে বক্রের ওপর অবস্থিত, তা হল—
View Solutionx−12=y+13=z−14 மற்றும் x−31=y−m2=z என்ற கோடுகள் ஒரு புள்ளியில் வெட்டிக் கொள்ளும் எனில், m-ன் மதிப்பைக் காண்க.
View Solution(2, 3, 6) என்ற புள்ளி வழிச் செல்வதும் x−12=y+13=z−31 மற்றும் x+32=y−3−5=z+1−3 என்ற கோடுகளுக்கு இணையானதுமான தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
View Solutionx−11=y−22=z−3m2 மற்றும் x−11=y−2m2=z−12 ஆகிய கோடுகள் ஒரே தளத்தில் அமைகின்றன. எனில், m-ன் வேறுபட்ட மெய்மதிப்புகளைக் காண்க.
View Solutionx−23=y+1−2,z=2 மற்றும் x−11=2y+33,z+52 என்ற கோடுகளுக்கு இடைப்பட்ட கோணம்.
View Solutionநேர்க்கோடுகள் x−32=y+54=z−1−13 மற்றும் x+13=y−45=z+22என்பது
View Solutionநேர்க்கோடுகள் x+22=y−3=z−14 மற்றும் x−3a=y−14=z−7a செங்குத்து எனில், (→a) -ன் மதிப்பு
View Solutionபொருத்துக: கோடுகளுக்கு x−14=2−y6=z−412,x−3−2=y−33=5−z6
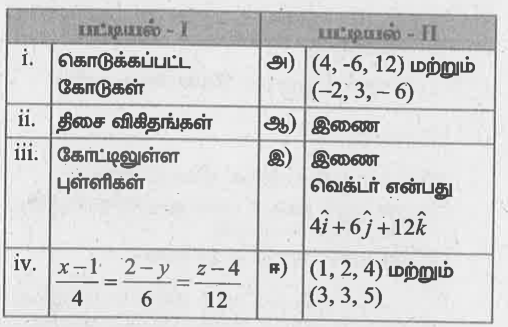
View Solutionx−13=y+12=z−15 மற்றும் x−24=y−13=z+1−2 வெட்டுவதில்லை எனக்காட்டுக.
View SolutionSolve (use matrix method): 2x−3y+3z=10, 1x+1y+1z=10, 3x−1y+2z=13.
View SolutionDetermine the term independent of a in the expansion of ⎛⎝a+1a23−a13+1−a−1a−a12⎞⎠10
View SolutionFind the value of x12.x32.x12÷x14
View SolutionFind the shortest distance between the lines frac[x][2]=frac[y][-3]=frac[z][1] and frac[x-2][3]=frac[y-1][-5]=frac[z+2][2] .
View Solution