तीन समतल
पर विचार कीजिए।
व क्रमशः समतलों व व एवं व की प्रतिच्छेदन रेखाएं है।
कथन1: रेखाओं व में से कम से कम दो रेखाएं असमांतर है।
कथन 2:तीनों समतलों का कोई भी उभयनिष्ठ बिंदु नहीं है।
वक्तव्य I सत्य है वक्तव्य II सत्य है, वक्तव्य II, वक्तव्य I का सही स्पष्टीकरण है
वक्तव्य I सत्य है वक्तव्य II सत्य है, वक्तव्य II, वक्तव्य I का सही स्पष्टीकरण नहीं है
वक्तव्य I सत्य है, वक्तव्य II असत्य है
वक्तव्य I सत्य है, वक्तव्य II सत्य है
The correct Answer is:C
Step by step video, text & image solution for तीन समतल P_(1):x-y+z=1 P_(2):x+y-z=-1 P_(3):x-3y+3z=2 पर विचार कीजिए। L_(1),L_(2) व L_(3) क्रमशः समतलों P_(2) व P_(3),P_(3) व P_(1) एवं P_(1) व P_(2) की प्रतिच्छेदन रेखाएं है। कथन1: रेखाओं L_(1),L_(2) व L_(3) में से कम से कम दो रेखाएं असमांतर है। कथन 2:तीनों समतलों का कोई भी उभयनिष्ठ बिंदु नहीं है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिविमीय ज्यामिति BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - त्रिविमीय ज्यामिति EXERCISE - विश्लेषणात्मक प्रश्न
4 Videos
- त्रिविमीय ज्यामिति BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - त्रिविमीय ज्यामिति EXERCISE - एकल पूर्णांक प्रश्न
1 Videos
- त्रिविमीय ज्यामिति BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - त्रिविमीय ज्यामिति EXERCISE - मैट्रिक्स -सुमेल प्रकार
2 Videos
- त्रिभुजों के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - त्रिभुजों के गुणEXERCISE - एकल पूर्णांक प्रश्न
1 Videos
- दीर्घवृत्त BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - दीर्घवृत्त EXERCISE - एकल पूर्णांक प्रश्न
1 Videos
Similar Questions
(i) बिन्दुओं (2, 1, 0), (5, 0, 1) तथा (4, 1, 1) से होकर जाने वाले तल का समीकरण ज्ञात कीजिए।
(ii) यदि बिन्दु P के निर्देशांक (2, 1, 6) हैं , तो बिन्दु Q ज्ञात कीजिए, जिसके लिए PQ तल (i) के लम्बवत है तथा PQ का मध्य-बिन्दु उस पर स्थित है।
View Solutionयदि समतल Ax−2y+z=d तथा रेखाओं x−12=y−23=z−34 एवं x−23=y−34=z−45 को अन्तर्विष्ट करने वाले समतल के बीच की दूरी √6, हो तो d का मान है
View Solutionमाना रैखिक समीकरणों ax+by+cz=0,bx+cy+az=0 तथा cx+ay+bz=0 हैं।
स्तम्भ I में दिए गए प्रतिबन्धों /व्यंजकों का स्तम्भ II में दिए गए कथनों के साथ सुमेल करायें।

View Solutionदिया है कि किसी त्रिभुज ABC के शीर्षों A,B एवं C की सम्मुख भुजाओं की लम्बाइयाँ क्रमशः a,b एवं c है | माना कि a = 6, b = 10 तथा त्रिभुज का क्षेत्रफल 15√3 है | यदि ∠ACB अधिक कोण (obtuse angle) है तथा त्रिभुज के अन्तः वृत्त की त्रिज्या r है, तो r2 का मान है |
View Solutionबिन्दु (h, 0) से गुजरने वाली एक ऊर्ध्वाधर रेखा दीर्घवृत्त x24+y23=1 को बिन्दुओं P तथा Q पर काटती है। माना कि बिन्दुओं P तथा Q पर दीर्घवृत्त की स्पर्शरेखाएँ बिन्दु R पर मिलती हैं । यदि Δ(h) = त्रिभुज PQR का क्षेत्रफल, Δ1=max1/2≤h≤1Δ(h) और Δ2=min1/2≤h≤1Δ(h) है तब 8√5Δ1−8Δ2=
View SolutionConsider the lines L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 and the planes P1=7x+y+2z=3,P2:3x+5y−6z=4. Let ax+by+cz=d be the equation of the plane passing through the point of intersection of lines L1andL2, and perpendicular to planes P1andP2.
Match Column I with Column II.

View SolutionP1andP2 are planes passing through origin, L1andL2 are two lines on P1andP2 respectivelym such that their intersection is the origin. Show that there exist points, A, B and C , whose perpmutation, A, B' and C' respectively, can be chosen such that (i) A is on L1'BandP1 put not on L1andC not on P1 , (ii) A is on L2,B'onP2 but not on L2andC' not on P2 .
View SolutionP1andP2 are planes passing through origin, L1andL2 are two lines on P1andP2 respectivelym such that their intersection is the origin. Show that there exist points, A, B and C , whose perpmutation, A, B' and C' respectively, can be chosen such that (i) A is on L1'BandP1 put not on L1andC not on P1 , (ii) A is on L2,B'onP2 but not on L2andC' not on P2 .
View SolutionConsider three planes P1:x−y+z=1
P2:x+y−z=−1
and P3:x−3y+3z=2
Let L1,L2,L3 be the lines of intersection of the planes P2 and P3,P3 and P1,P1 and P2 respectively.
Statement I Atleast two of the lines L1,L2 and L3 are non-parallel.
Statement II The three planes do not have a common point.
View SolutionConsider two intersecting (non-perpendicular lines L1=0andL2=0 and a point P1. Image of P1 and L1=0 is P2, image of P2 in L2=0 is P3 , image of P3 in L1 =0 is P4 and so on. Which of the following statements are incorrect ?
View SolutionLet P1andP2 be two planes containing the lines L2andL2 respectively.
STATEMENT-1 : If P1andP2 are parallel then L1andL2 must be parallel.
and
STATEMENT-2 : If P1andP2 are parallel the L1andL2 may not have a common point.
View Solutionतीन समतल लीजिए
P1:x−y+z=1
P2:x+y−z=−1
P3:x−3y+3z=2
माना L1,L2,L3 क्रमशः समतल P2 व P3,P3 व P1 तथा P1 व P2 की प्रतिच्छेदी रेखायें हैं।
कथन-1: L1,L2 और L3 में से कम से कम दो रेखायें असमान्तर हैं।
क्योंकि कथन - 2 : तीनों समतलों का कोई सर्वनिष्ठ बिन्दु नहीं है।
View SolutionNumber of units of three different products P1,P2andP3 produced (nits in hundreds) at four different locations (L1,L2=L3andL4)
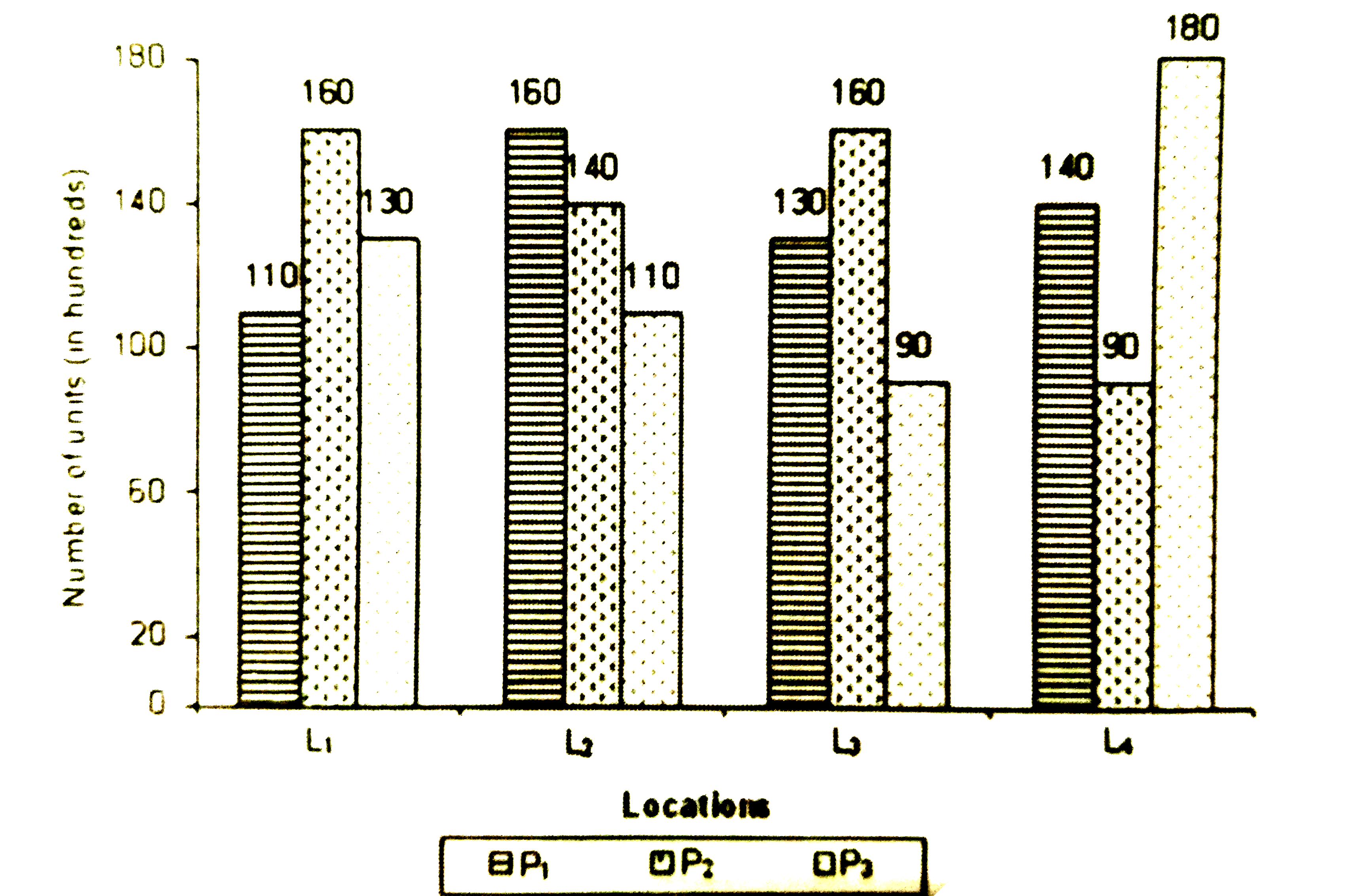
What is the total number of units P2 produced (in hundreds) in the four locations together) ?
View SolutionNumber of units of three different products P1,P2andP3 produced (nits in hundreds) at four different locations (L1,L2=L3andL4)
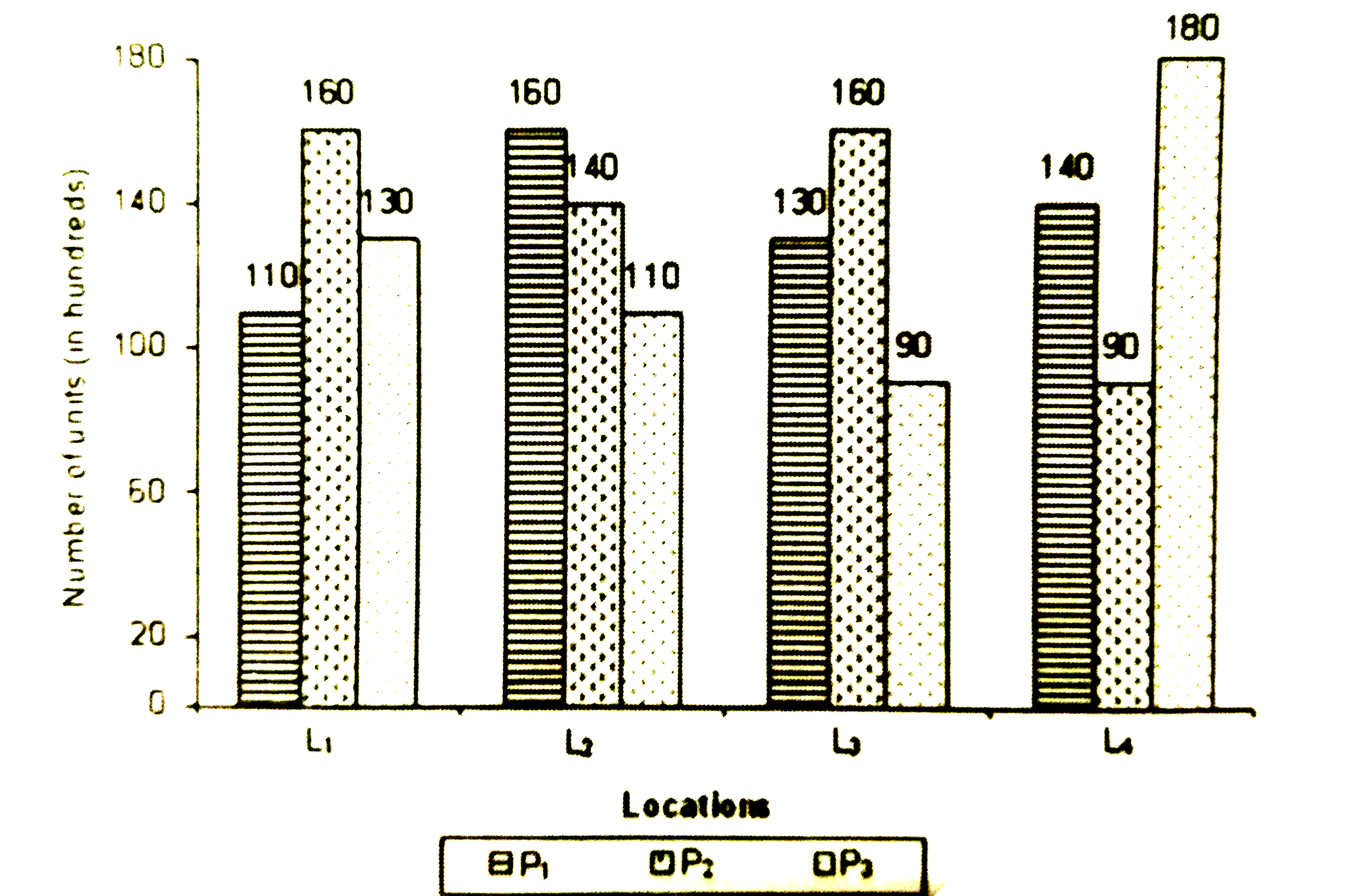
What is the average number of units (in hundreds of P1 produced per location ?
View SolutionConsider the lines L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 and the planes P1=7x+y+2z=3,P2:3x+5y−6z=4. Let ax+by+cz=d be the equation of the plane passing through the point of intersection of lines L1andL2, and perpendicular to planes P1andP2.
Match Column I with Column II.

View Solution
