एक पतले ठोस लकड़ी के फलक से एक त्रिभुज ABC काटा गया हैं (चित्र देखिए) दर्शाए गये अनुसार D, E तथा F इसकी भुजाओं के मध्य बिन्दु हैं तथा G त्रिभुज का केन्द्र है। G से गुजरने वाली तथा त्रिभुज के समतल के लम्बवत् अक्ष के सापेक्ष त्रिभुज का जडत्व आघूर्ण I0. है। यदि छोटा त्रिभुज DEF त्रिभुज ABC में से निकाल लिया जाये तो शेष बचे हुए भाग का उसी अक्ष के सापेक्ष जडत्व आघूर्ण है। तब
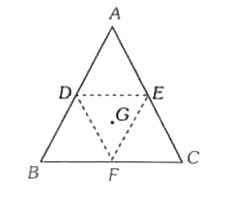
I=916I0
I=1516I0
I=34I0
I=I04
The correct Answer is:B
Step by step video & image solution for एक पतले ठोस लकड़ी के फलक से एक त्रिभुज ABC काटा गया हैं (चित्र देखिए) दर्शाए गये अनुसार D, E तथा F इसकी भुजाओं के मध्य बिन्दु हैं तथा G त्रिभुज का केन्द्र है। G से गुजरने वाली तथा त्रिभुज के समतल के लम्बवत् अक्ष के सापेक्ष त्रिभुज का जडत्व आघूर्ण I_(0). है। यदि छोटा त्रिभुज DEF त्रिभुज ABC में से निकाल लिया जाये तो शेष बचे हुए भाग का उसी अक्ष के सापेक्ष जडत्व आघूर्ण है। तब by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सॉल्वड पेपर (JEE MAIN 2019)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर (JEE MAIN 2019)EXERCISE - 11 Jan, Shift-II (JANUARY ATTEMPT)
30 Videos
- सॉल्वड पेपर (JEE MAIN 2019)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर (JEE MAIN 2019)EXERCISE - 12 Jan, Shift-I (JANUARY ATTEMPT)
30 Videos
- सॉल्वड पेपर (JEE MAIN 2019)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर (JEE MAIN 2019)EXERCISE - 10 Jan, Shift-II (JANUARY ATTEMPT)
30 Videos
- सामान्य भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सामान्य भौतिकी EXERCISE - विश्लेषणात्मक प्रश्न
9 Videos
- सॉल्वड पेपर (JEE MAIN 2021)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर (JEE MAIN 2021)EXERCISE - Physics (Section B)
10 Videos
Similar Questions
दिखाए गए चित्रानुसार मीटर सेतु के एक प्रयोग में A से 40cm दूरी पर शून्य प्राप्त होता है। यदि 10Ω के एक प्रतिरोध को R1 के साथ श्रेणीक्रम में लगाते है, तो शून्य बिंदु 10cm विस्थापित हो जाता है। वह प्रतिरोध, जिसको (R1+10)Ω के साथ समान्तर क्रम में लगाने से शून्य बिंदु पुनः अपनी आरम्भिक स्थिति में आ जाता है, होना चाहिए
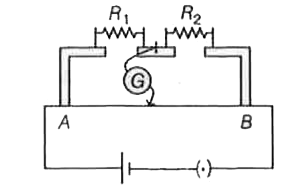
View Solution(25W,220V) तथा (100W,220V), रेटिंग के दो बिजली के बल्बों को एक 220 V के स्त्रोत के साथ श्रेणीक्रम में लगाया गया है। यदि 25W तथा 100 W के बल्ब द्वारा ली गई शक्ति का मान क्रमशः P1 तथा P2 है, तो
View Solutionदो बल P तथा Q, जिनके परिमाण क्रमशः 2F तथा 3F है, परस्पर θ कोण बनाते है। यदि बल Q को दोगुना कर दे, तो इनका परिणामी बल भी दोगुना हो जाता है। तब कोण होगा
View Solutionनीचे दी गई राशियों के MKS पद्धति में मात्रक बताइए।
(i) यंग प्रत्यास्थता गुणांक
(ii) चुम्बकीय प्रेरण
(iii) लेन्सों की क्षमता
View SolutionN2 गैस को औसत रेखीय गतिज ऊर्जा ___∘ सेल्सियस ताप पर विरामावस्था से 0.1 Volt विभवान्तर से त्वरित इलेक्ट्रान के गतिज ऊर्जा के बराबर होती है। (दिया है kB=1.38×10−23J/K) (नकटतम् पूर्णांक तक भरिये)
View Solutionयदि मूलबिंदु O के सापेक्ष त्रिभुज ABC के शीर्षों के स्थिति सदिश क्रमशः (1,−1,2),(2,1,3) और (−1,2,−1) है| तथा इसके केन्द्रक का स्थिति सदिश ज्ञात कीजिए|
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है। यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2) हो तो त्रिभुज की शेष दो भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionसदिशों के योग का त्रिभुज तथा समांतर चतुर्भुज नियम
View SolutionList - I List - II (A) बिन्दु (2, - 2), (- 2, 1) तथा (5, 2) (P) एक समकोणीय त्रिभुज के शीर्ष है (B) बिन्दु (1, - 2), (-3, 0) तथा (5, 6)(Q) एक समकोणीय समद्विबाहु त्रिभुज के शीर्ष है (C) बिन्दु (3,7), (6,5) तथा (15,-1)(R) एक समबाहु त्रिभुज के शीर्ष है (D) बिन्दु (2,2), (-2, -2) तथा (−2√3,2√3)(S) कोई त्रिभुज नहीं बनाते है
View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
View Solution
