Sketch the region bounded by the curves y=x2andy=21+x2 . Find the area.
Video Solution
Text Solution
The given curves are y=x2 (1)
and y=21+x2 (2)
Solving (1) and (2), we have
x2=21+x2
or x4+x2−2=0
or (x2−1)(x2+2)=0
or (x2−1)(x2+2)=0
or x=±1
Also, y=21+x2 is an even function.
Hence, its graph is symmetrical about y-axis.
At x = 0, y = 2, by increasing the values of x,y decreases and when x→∞,y→0.
Therefore, y=0 is an asymptote of the given curve.
Thus, the graphs of the two curves are as follows :
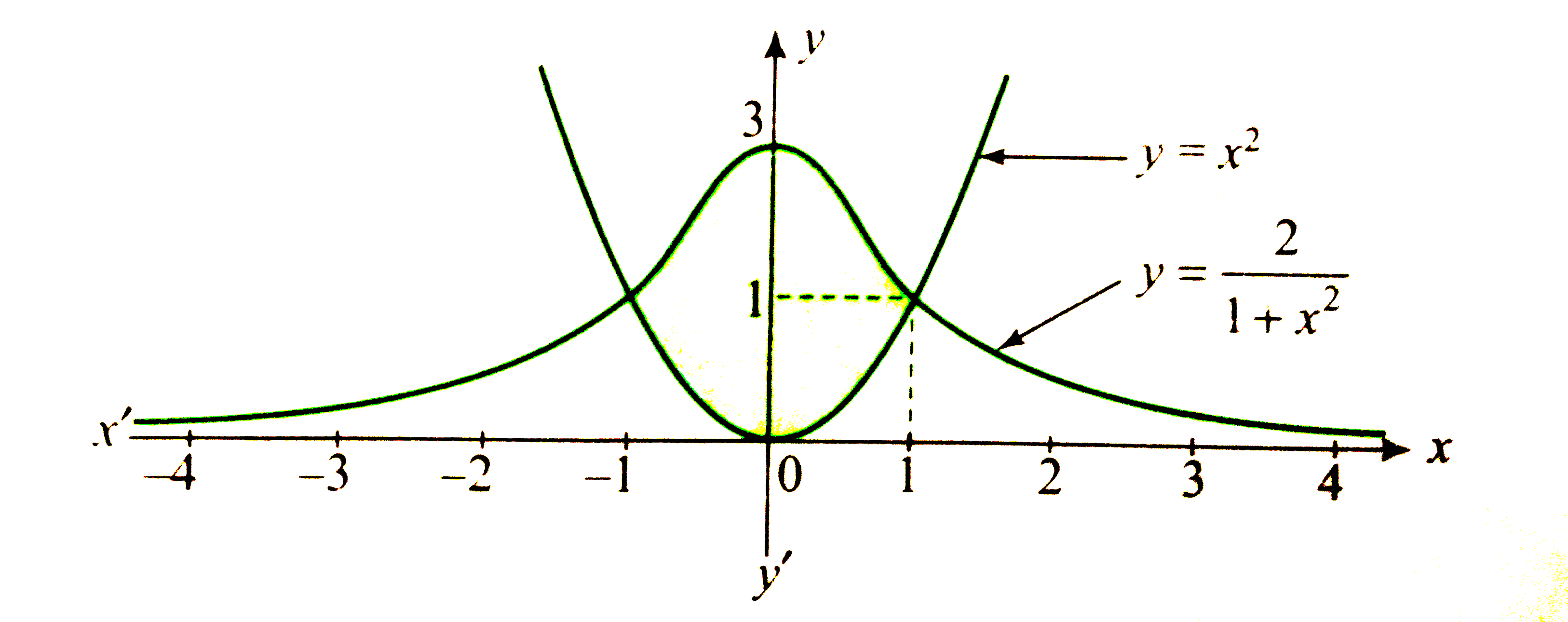
Required area =2∫10(21+x2−x2)dx
=(4tan−1x−2x33)0
=π−23 sq. units.
|
Similar Questions
Knowledge Check
The area of the region bounded by the curves y=x2 and x=y2 is
A13B12C14D3
Sketch the region bounded by the curves y=√5−x2 and y=|x−1| and find its area.
View SolutionIndicate the region bounded by the curves y=x2,y=x+2 and x-axis and obtain the area enclosed by them
View SolutionSketch the region bounded by the curves y=logexandy=(logex)2. Also find the area of the region.
View SolutionFind by integration the area of the region bounded by the curve y=2x−x2 and the x-axis.
View SolutionIndicate the region bounded by the curves x2=y,y=x+2 and x-axis and the area enclosed by them is …...........
View SolutionFind the area of the region bounded by the curves y=√x+2andy=1x+1 between the lines x=0 and x=2.
View SolutionFind the area of the region bounded by the curve y=(x2+2)2, the X-axis and the lines x=1andx=3.
View Solution
