Sketch the region bounded by the curves y=x2andy=21+x2 . Find the area.
The given curves are y=x2 (1)
and y=21+x2 (2)
Solving (1) and (2), we have
x2=21+x2
or x4+x2−2=0
or (x2−1)(x2+2)=0
or (x2−1)(x2+2)=0
or x=±1
Also, y=21+x2 is an even function.
Hence, its graph is symmetrical about y-axis.
At x = 0, y = 2, by increasing the values of x,y decreases and when x→∞,y→0.
Therefore, y=0 is an asymptote of the given curve.
Thus, the graphs of the two curves are as follows :
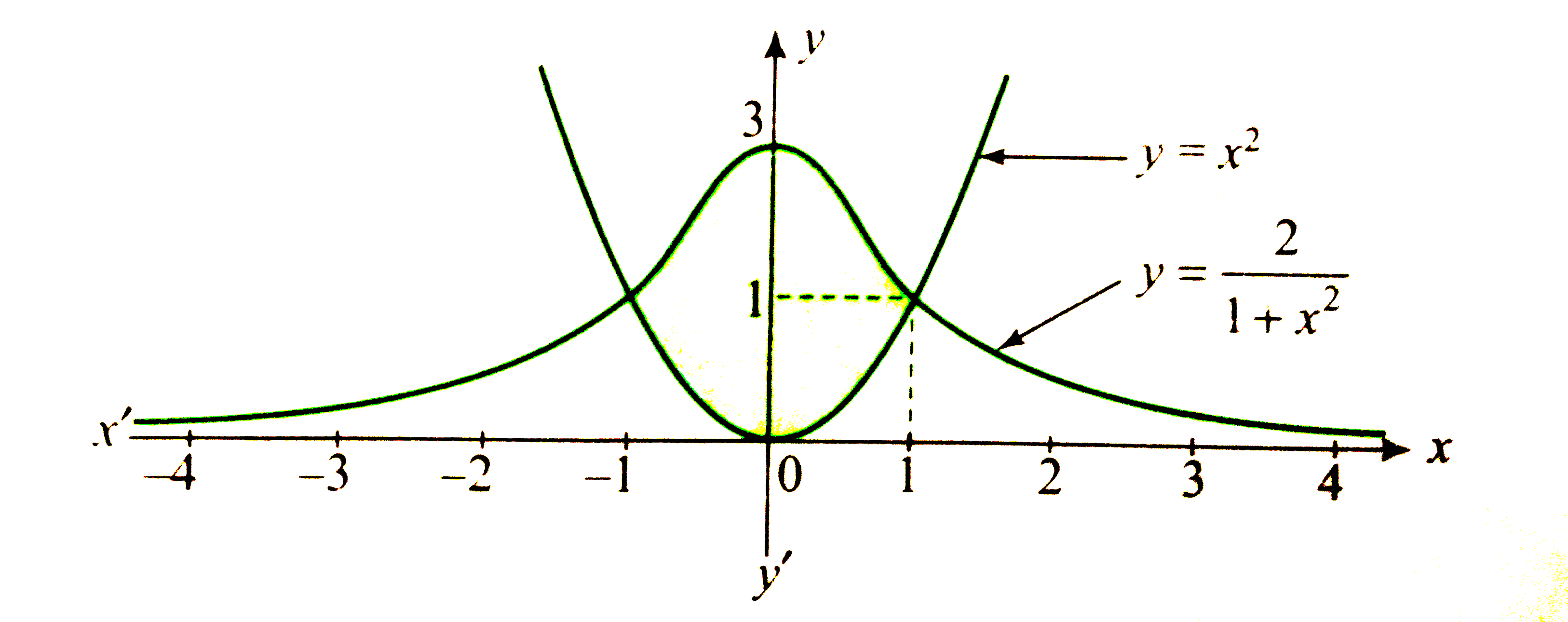
Required area =2∫10(21+x2−x2)dx
=(4tan−1x−2x33)0
=π−23 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
Sketch the region bounded by the curves y=√5−x2 and y=|x−1| and find its area.
View SolutionFind the area bounded by the curves y=6x−x2andy=x2−2x.
View SolutionThe area of the region bounded by the curves y=x2andy=21+x2 is
View SolutionSketch the curves and identify the region bounded by the curves x=12,x=2,y=logxany=2x. Find the area of this region.
View SolutionExamples: Find the area of the region bounded by the curve y2=2y−x and the y-axis.
View SolutionA body weighs w Newton on the surface of the earth. Its weight at a height equal to half the radius of the earth, will be xyw where x and y are coprimes . Find x and y
View SolutionSketch the region bounded by the curves y=x2+2, y=x, x=0 and x=1. also, find the area of this region.
View SolutionFind by integration the area of the region bounded by the curve y=2x−x2 and the x-axis.
View SolutionFind by integration the area of the region bounded by the curve y=2x−x2 and the x-axis.
View SolutionThe area (in sq. units) of the region bounded by the curves y=2−x2andy=|x| is k, then the value of 3k is
View Solution
