The region between y =0 and y=d constains a magnetic field →B=B→z. A particle of mass m and charge q enters of the region with a velocity →v=v→i. If d=mv2qB the acceleration of the charged particle at the point of its emergence at the other side is :
qvBm(12ˆi−√32ˆj)
qvBm(√32ˆi−12ˆj)
qvBm(−ˆj+ˆi√2)
qvBm(ˆi+ˆj√2)
To solve the problem, we need to analyze the motion of a charged particle in a magnetic field and determine its acceleration at the point of emergence from the field.
1. Understanding the Motion:
The charged particle with mass m and charge q enters a magnetic field →B=B^z with an initial velocity →v=v^i. The magnetic field is directed along the z-axis, while the particle moves along the x-axis.
2. Radius of Circular Motion:
When a charged particle moves perpendicular to a magnetic field, it experiences a magnetic force that causes it to move in a circular path. The radius r of this circular motion can be derived from the centripetal force equation:
mv2r=qvB
Rearranging gives:
r=mvqB
3. Given Condition:
We are given that d=mv2qB. This implies that the radius of the circular motion is:
r=2d
Substituting d gives:
r=2(mv2qB)=mvqB
This confirms our earlier expression for the radius.
4. Emergence from the Magnetic Field:
The particle will emerge from the magnetic field after traveling a distance d in the y-direction. Since the radius of the circular path is r=2d, the center of the circular path lies at a distance d from the y = 0 line.
5. Calculating the Angle of Emergence:
As the particle moves through the magnetic field, it will exit at an angle θ with respect to the horizontal. Using the geometry of the situation:
cosθ=dr=d2d=12
Thus, θ=60∘.
6. Velocity Components at Emergence:
The velocity components at the point of emergence can be calculated as:
vx=vcos(60∘)=v2
vy=−vsin(60∘)=−v√32
7. Finding the Acceleration:
The magnetic force acting on the particle is given by:
→F=q→v×→B
The acceleration →a can be expressed as:
→a=→Fm=qm(→v×→B)
Substituting →v=(v2^i−v√32^j) and →B=B^k:
→v×→B=(v2^i−v√32^j)×(B^k)
Using the right-hand rule for the cross product:
→v×→B=vB2^j+vB√32^i=vB2^j+√3vB2^i
8. Final Acceleration Expression:
Therefore, the acceleration becomes:
→a=qBm(v2^j+√3v2^i)
Simplifying gives:
→a=qvB2m(√3^i+^j)
Final Result:
The acceleration of the charged particle at the point of its emergence is:
→a=qvB2m(√3^i+^j)
The charged particle with mass m and charge q enters a magnetic field →B=B^z with an initial velocity →v=v^i. The magnetic field is directed along the z-axis, while the particle moves along the x-axis.
When a charged particle moves perpendicular to a magnetic field, it experiences a magnetic force that causes it to move in a circular path. The radius r of this circular motion can be derived from the centripetal force equation:
mv2r=qvB
Rearranging gives:
r=mvqB
We are given that d=mv2qB. This implies that the radius of the circular motion is:
r=2d
Substituting d gives:
r=2(mv2qB)=mvqB
This confirms our earlier expression for the radius.
The particle will emerge from the magnetic field after traveling a distance d in the y-direction. Since the radius of the circular path is r=2d, the center of the circular path lies at a distance d from the y = 0 line.
As the particle moves through the magnetic field, it will exit at an angle θ with respect to the horizontal. Using the geometry of the situation:
cosθ=dr=d2d=12
Thus, θ=60∘.
The velocity components at the point of emergence can be calculated as:
vx=vcos(60∘)=v2
vy=−vsin(60∘)=−v√32
The magnetic force acting on the particle is given by:
→F=q→v×→B
The acceleration →a can be expressed as:
→a=→Fm=qm(→v×→B)
Substituting →v=(v2^i−v√32^j) and →B=B^k:
→v×→B=(v2^i−v√32^j)×(B^k)
Using the right-hand rule for the cross product:
→v×→B=vB2^j+vB√32^i=vB2^j+√3vB2^i
Therefore, the acceleration becomes:
→a=qBm(v2^j+√3v2^i)
Simplifying gives:
→a=qvB2m(√3^i+^j)
The acceleration of the charged particle at the point of its emergence is:
→a=qvB2m(√3^i+^j)
Topper's Solved these Questions
Similar Questions
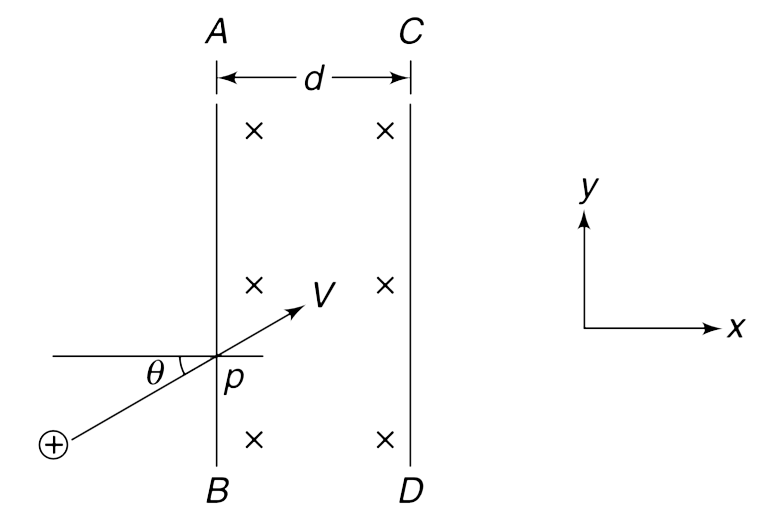
AB and CD are two parallel planes perpendicular to the X axis. There is a uniform magnetic field (B) in the space between them directed in negative Z direction. Width of the region having field is d and rest of the space is hav- ing no field. A particle having mass m and charge + q enters the region with a velocity V making an angle q with the X direction as shown.
(a) Find the values of d for which the particle will come out of the magnetic field crossing CD.
(b) For d=(√2−12)mvqB and 0=π6 find the angular deviation in the path of the particle.
(c) Find the deviation in path of the particle if d=5mv4qB(1−sin0)
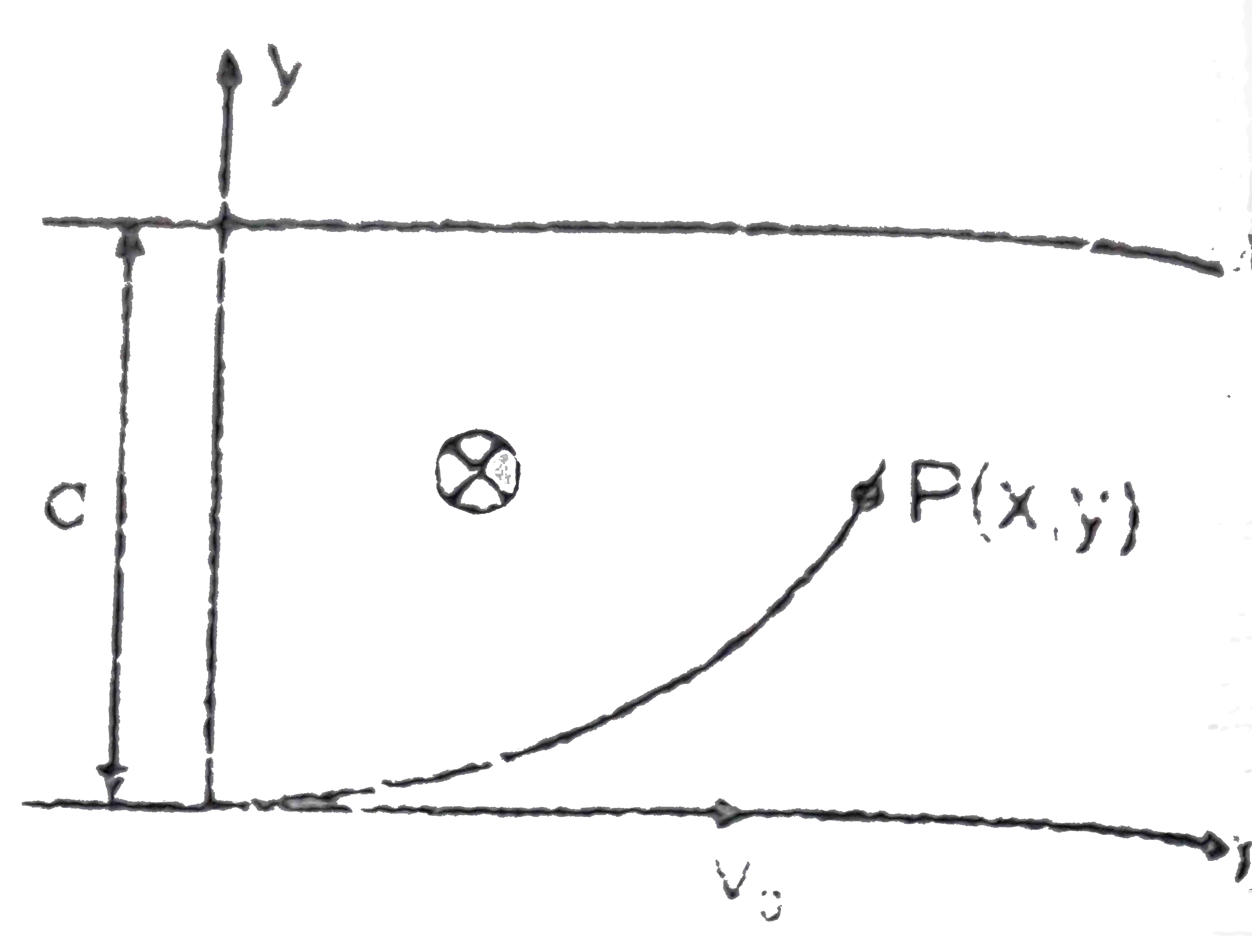
View SolutionA non-uniform magnetic field →B=B0(1+yd)(−ˆk) is present in region of space in between y=0&y=d.The lines are shown in the diagram.A particle of mass m and positive charge q is moving.Given an initial velocity →v=v0ˆi.Find the components of velocity of the particle when it leaves the field.
View Solution
Knowledge Check
A charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
AmvsinθqBBmvqBsinθCmvqBDmvtanθqBA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
AAways circularBcircular, If v×B=0Ccircular,If v.B=0DNone of theseA particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v, The radius of the circular path described by it will be
ABq/mvBmq/BvCmB/qvDmv/Bq
A particle of mass m and charge q moving with velocity v enters the region of uniform magnetic field at right angle to the direction of its motion. How does its kinetic energy get affected?
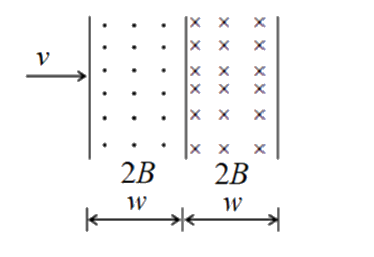
View SolutionThe figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
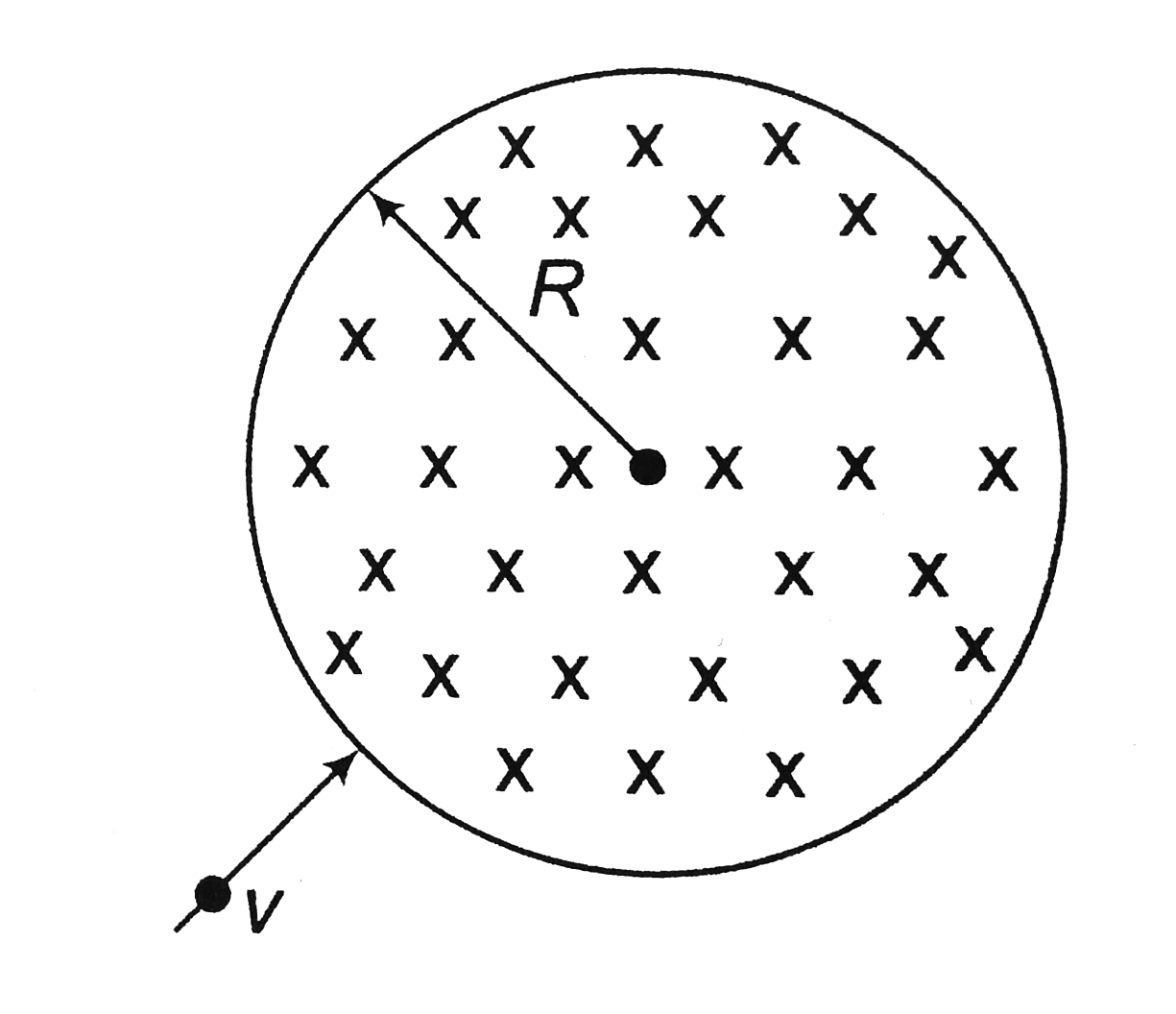
View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is

View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is

View Solution
