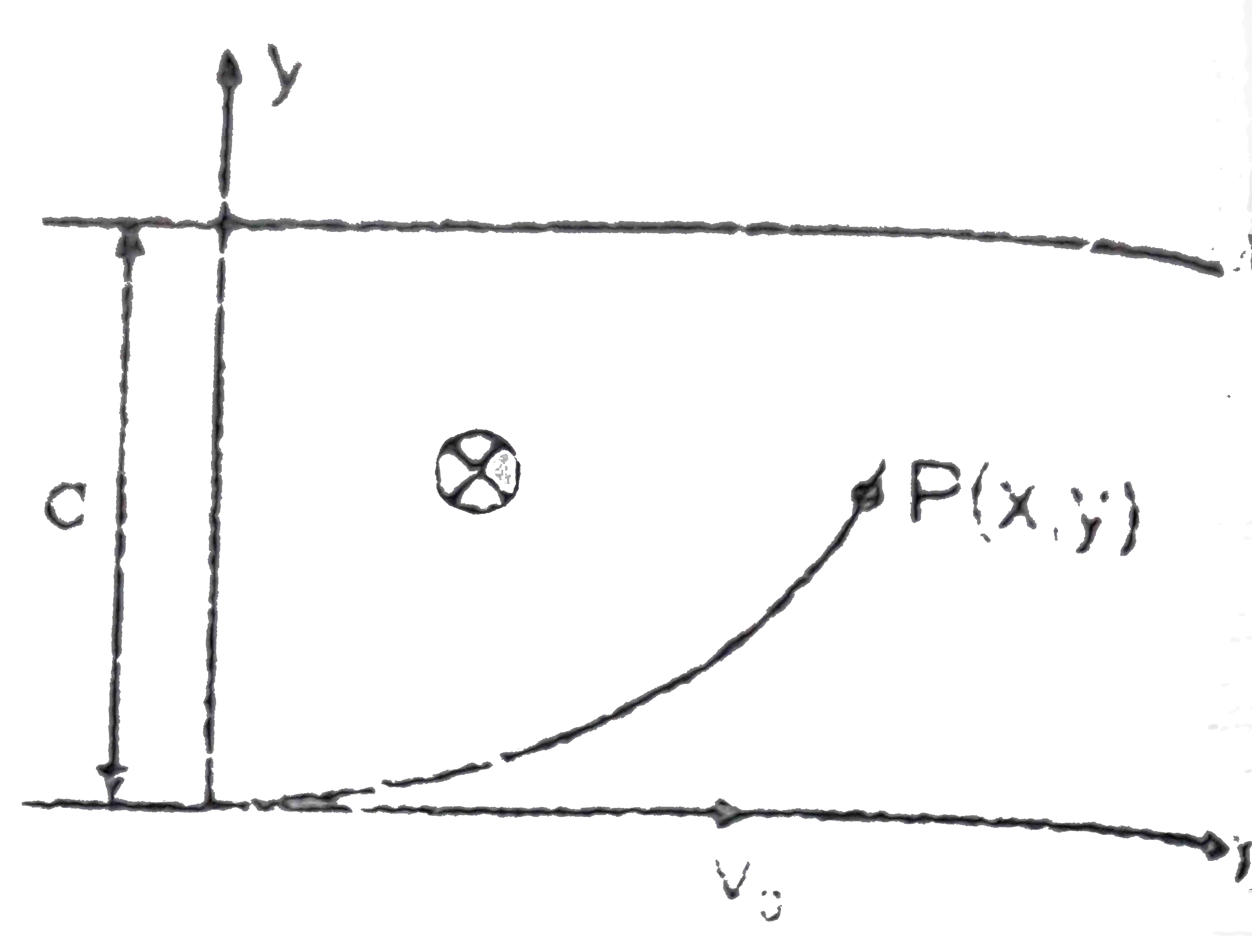
A non-uniform magnetic field $\to B = B_{0} (1 + \frac{y}{d}) (- ˆ k)$ is present in region of space in between $y = 0 & y = d$ .The lines are shown in the diagram.A particle of mass $m$ and positive charge $q$ is moving.Given an initial velocity $\to v = v_{0} ˆ i$ .Find the components of velocity of the particle when it leaves the field.

Text Solution

Verified by Experts

The correct Answer is: $V_{x} = V_{0} - \frac{3 q B_{0} d}{2 m}$ and $V_{y} = {\sqrt{V_{0}^{2} - (V_{0} - \frac{3 q B_{0}}{2 m} d)}}^{2}$

Let at time $t$ particle be at point $P (x, y)$ and its velocity be
$\to B = (V_{x} ˆ i + V_{y} ˆ j)$
$∣ ∣ \to V ∣ ∣ = ∣ ∣ {\to V}_{0} ∣ ∣ \Rightarrow V_{0}^{2} = V_{x}^{2} + V_{y}^{2}$
(work done by magnetic field is always zero so charge in magnitude of velocity)Then, magnetic force on the particle at point $P$ is
$\to F = q (V_{x} ˆ i + V_{y} ˆ j) . B_{0} (1 + \frac{y}{d}) (- ˆ k) \Rightarrow - q B_{0} [1 + \frac{y}{d}] d y = m d v_{x}$
Now when the particle will be coming out of the at that point $y = d$ .Let the velocity in $x$ -direction be $V_{x}$ then integrating we get,
$V_{x} \int V_{0} d v_{x} = - \frac{q B_{0}}{m} d \int 0 d y = - \frac{q B_{0}}{m} [d + \frac{d^{2}}{2 d}] = - \frac{3 q B_{0} d}{2 m}$
so $V_{x} = V_{0} - \frac{3 q B_{0} d}{2 m}$
$\Rightarrow V_{y} = \sqrt{V_{0}^{2} - V_{x}^{2}}$
$\Rightarrow V_{y} = {\sqrt{V_{0}^{2} - (V_{0} - \frac{3 q B_{0}}{2 m} d)}}^{2}$

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Knowledge Check

A non-uniform magnetic field $\to B = B_{0} (1 + \frac{y}{d}) (- ˆ k)$ is present in the region of space between $y = 0$ and $y = d$ . A particle of mass $m$ and positive charge $q$ has velocity $\to v = \frac{3 q B_{0} d}{m} ˆ i$ at origin $O$ . Find the angle made by velocity of the particle withe the positive $x$ -axis when it leaves the field. (Ignore any interaction other than magnetic field)
A $90^{\circ}$
B $30^{\circ}$
C $60^{\circ}$
D $45^{\circ}$
There exist uniform magnetic field $\to B = - B_{0} ˆ k$ in region of space with $0 < x < d$ and $2 d < x < 3 d$ as shown in the figure. A positive charged particle of mass $m$ and charge $q$ is projected with velocity $\to v = v ˆ i$ as shown in the figure. If radius of curvature of path of the charged particle in magnetic field is $R (2 d < R < 3 d)$ then time elapse by charged particle in magnetic field regions is
A $\frac{m}{2 q B}$
B $2 \frac{m}{q B} {sin}^{- 1} (\frac{d}{R})$
C $\frac{m}{q B}$
D $\frac{m}{q B} {sin}^{- 1} (\frac{d}{R})$
There exist uniform magnetic field $\to B = - B_{0} ˆ k$ in region of space with $0 < x < d$ and $2 d < x < 3 d$ as shown in the figure. A positive charged particle of mass $m$ and charge $q$ is projected with velocity $\to v = v ˆ i$ as shown in the figure. If radius of curvature of path of the charged particle in magnetic field is $R (2 d < R < 3 d)$ then time elapse by charged particle in magnetic field regions is
A $\frac{m}{2 q B}$
B $\frac{m}{q B} {sin}^{- 1} (\frac{2 d}{R})$
C $\frac{m}{q B}$
D $\frac{m}{q B} {sin}^{- 1} (\frac{d}{R})$

RESONANCE-ELECTRODYNAMICS-Advanced level problems

Home
Ask Doubt
Profile

A non-uniform magnetic field →B=B0(1+yd)(−ˆk) is present in region of space in between y=0&y=d.The lines are shown in the diagram.A particle of mass m and positive charge q is moving.Given an initial velocity →v=v0ˆi.Find the components of velocity of the particle when it leaves the field.

The correct Answer is:Vx=V0−3qB0d2m and Vy=√V20−(V0−3qB02md)2

Topper's Solved these Questions

Similar Questions

Knowledge Check

RESONANCE-ELECTRODYNAMICS-Advanced level problems

The correct Answer is: $V_{x} = V_{0} - \frac{3 q B_{0} d}{2 m}$ and $V_{y} = {\sqrt{V_{0}^{2} - (V_{0} - \frac{3 q B_{0}}{2 m} d)}}^{2}$