If the median of the distribution given below is 28.5, find the values of x and y.
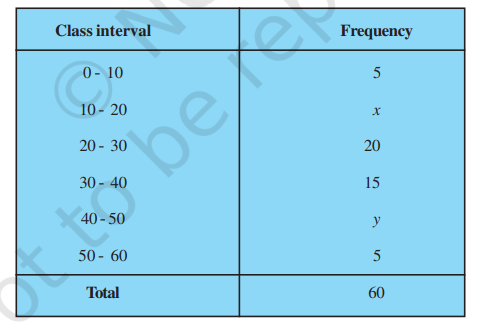
it can be observed that n=60
n/2 = 30
45+x+y=60
x+y=15.....(i)
The median of the data is given as 28.5 which lies in interval 20−30.
Therefore, median class = 20−30
Class size, h=10
Lower limit of median class, l=20
Frequency of median class, f=20
Cumulative frequency of class preceding the median class, cf = 5 + x
Median=l+[n2−cff]×h
28.5=20+⎡⎣602−(5+x)20⎤⎦×10
8.5=25−x2
25−x=8.5×2
x=25−17
x=8
Putting x=8 in equation (i)
8+y=15
y=7
Similar Questions
If the median of the distribution given below is 28.5, find the value of x and y
 View Solution
View SolutionIf the median of the distribution given below is 28.5, find the value of x and y . Class interval: 0-10 10-20 20-30 30-40 40-50 50-60 No. of students: 5 x 20 15 y 5
View SolutionThe median of the distribution given below is 14.4. Find the values of x and y, if the total frequency is 20.
 View Solution
View SolutionThe median of the following distribution is 35, find the value of a and b.
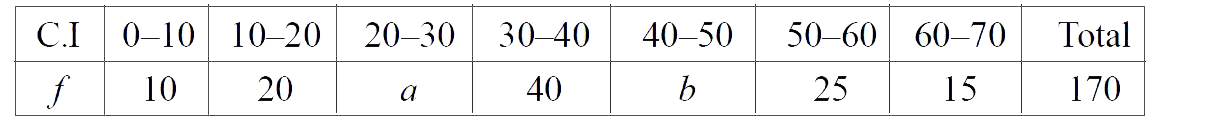 View Solution
View SolutionIn the distribution given below, Find the modal class is:
 View Solution
View SolutionIn each case given below find the value of x.
 View Solution
View SolutionIf the median of the following frequency distribution is 32.5 . Find the value of p :
 View Solution
View SolutionIf the median of the following frequency distribution is 32.5 . Find the value of p :
 View Solution
View SolutionIf the median of the following frequency distribution is 525, in the table given below, find the value of x and y. if total frequency is 100.
 View Solution
View SolutionFind the median of the following distribution
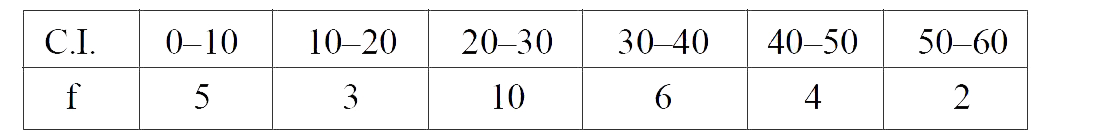 View Solution
View Solution

