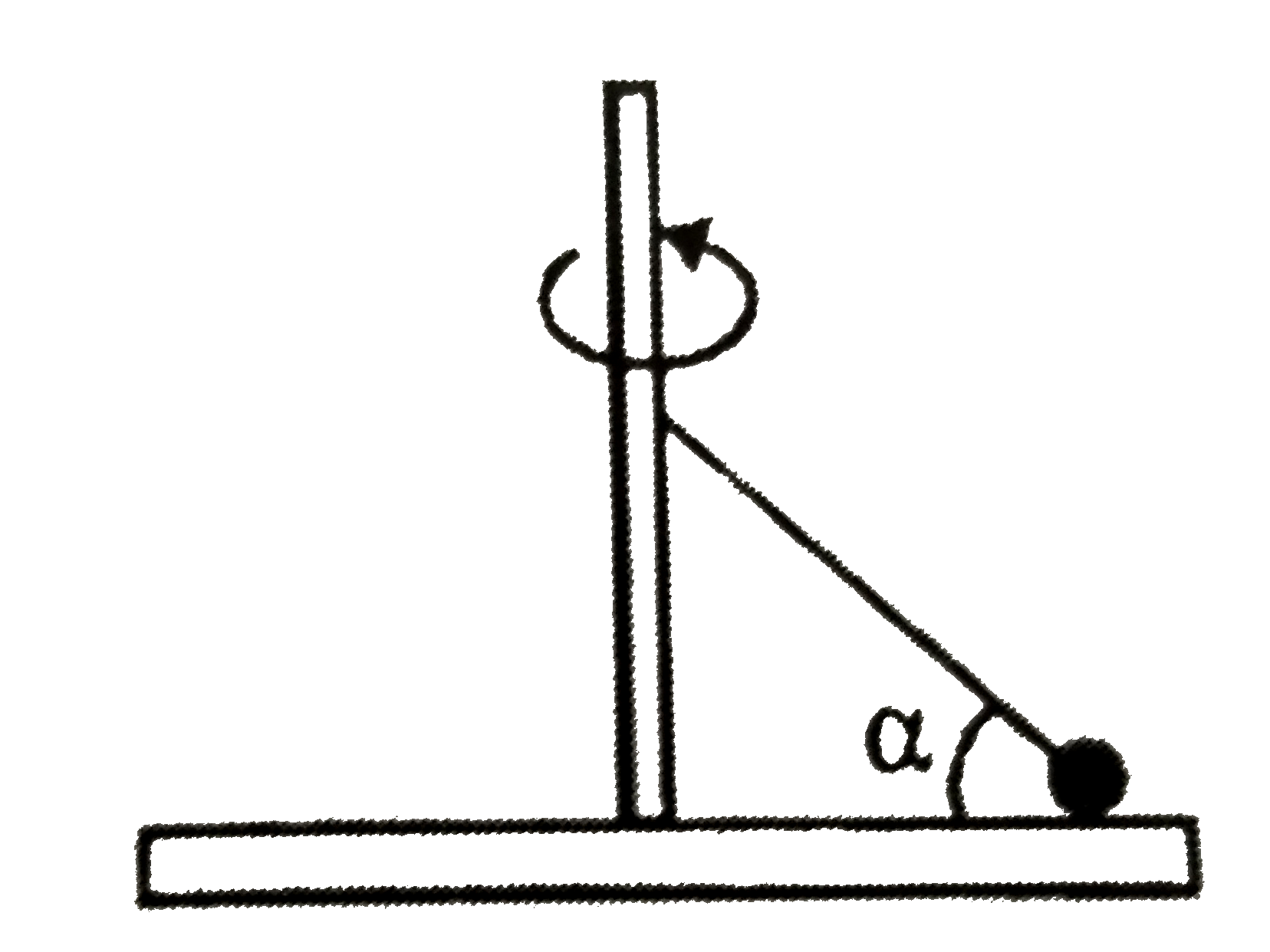
A circular platform rotates around a vertical axis with angular velocity ω=10rad/s. On the platform is a ball of mass 1kg, attached to the long axis of the platform by a thin of length of 10cm (α=30∘). Find normal force exerted by the ball on the platform (in newton). Friction is absent.
The correct Answer is:5
Step by step video, text & image solution for A circular platform rotates around a vertical axis with angular velocity omega=10rad//s. On the platform is a ball of mass 1kg, attached to the long axis of the platform by a thin of length of 10cm (alpha=30^(@)). Find normal force exerted by the ball on the platform (in newton). Friction is absent. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(S-2)6videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-1)22videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (S-1)10videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question1videos
BASIC MATHS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
Similar Questions
A circular platform rotates around a vertical axis with angular velocity ω=10rads. On the platform is a' ball of mass 2kg, attached to the long axis of the platform by a thin rod of length 16cm(α=30∘). Find the normal force (in N ). exerted by the ball on the platform. Assume friction is absent.
'(##CEN_KSR_PHY_JEE_C07_019_Q10##)'View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O wth an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.View Solution
Knowledge Check
- Question 1 - Select One
A circular of radius 20 cm is rotating about its own axis at an angular velocity ω . The angular velocity of a particle 'A' which is at a distance 10 cm from the axis of rotation is
A2ωBω/2CωDω/4 - Question 2 - Select One
A thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity ω. The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
AωM(m+M)Bω(M−2M)(M+2m)CωM(M+2m)Dω(M+2m)M - Question 3 - Select One
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity ω0 . When the tortoise moves along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform will vary with time t as
A B
B C
C D
D
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform Now, the platform is given an angular velocity ω0. When the tortoise moves along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform will vary with time t as -
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its center. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity c.o0. When the tortoise moves along the diameter of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform ω(t) will vary with time t as
View SolutionA cricket ball of mass 0.5 kg strikes a circket bat normally with a velocity of 20 m s−1 and rebounds with a velocity of 10 m s−1. The impulse of the force exerted by the ball on the bat is
View Solution

