A mass m rotating freely in a horizontal circle of a radius 1m on a frictionless smooth table support a stationary mass 2m, attached to the other end of the string passing through smooth hole O in table, hanging vertically. Find the angular velocity of rotation.
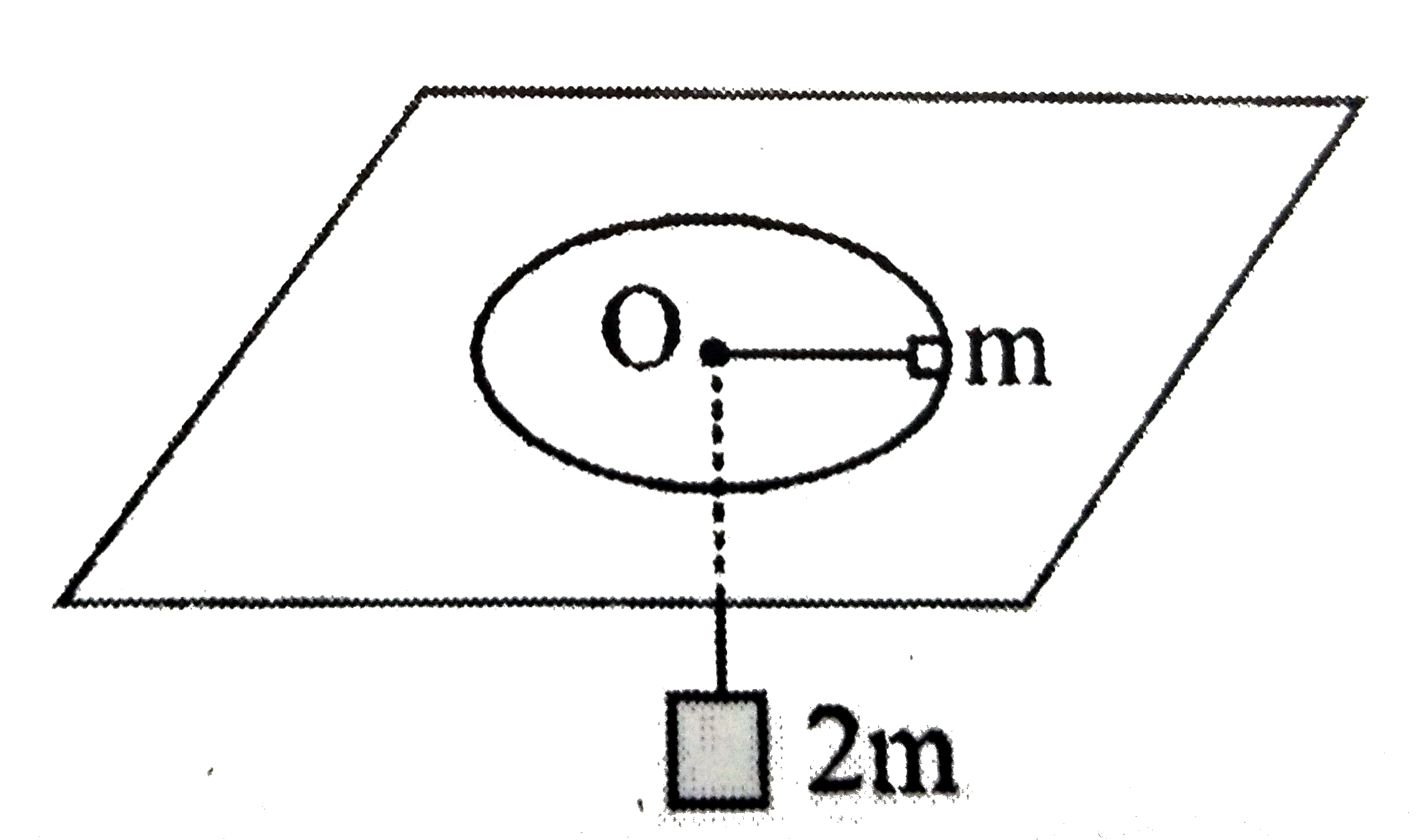
The correct Answer is:√2grad/s
Step by step video, text & image solution for A mass m rotating freely in a horizontal circle of a radius 1m on a frictionless smooth table support a stationary mass 2m, attached to the other end of the string passing through smooth hole O in table, hanging vertically. Find the angular velocity of rotation. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(S-2)
6 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-1)
22 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (S-1)
10 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
Similar Questions
An air puck of mass m1 is tied to a string allowed to revolved in a circle of radius R on a frictionless horizontal table . The other end of the string passes through a small hole in the centre of the table , and a load of mass m2 is tied to the string? The suspended load remains in equilibrium while the pack on the tabletop revolves.

a. Find the tension in the string
b. Find the radial force acting on the puck
c. Find the speed of the puck
d. Qualitaively describe what will happen in the monsion of the puck if the value of m2 is somewhat increased by placing an additional load on it.
e.Qualitaively describe what will happen in the monsion of the puck if the value of m2 is instead decreased removing a part from the hanging load.
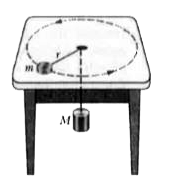
View SolutionA puck of mas m=1.50 kg slides in a circle of radius r=25.0 cm on a frictionless table while attached to a hanging cylinder of mass M=2.50 kg by means of a cord that extends through a hole in the table. What speed keeps the cylinder at rest?
View Solution
Knowledge Check
A metal wire of negligible mass, length 1 m and cross-sectional area 10−6m2 is kept on a smooth horizontal table with one end fixed on the table. A ball of mass 2kg is attached to the other end of the wire. When the wire and the ball are rotated with angular velocity of 20 rad/s, it is found that the wire is elongated by 10−3m. If the Young's modulus of the metal is n×1011N/m2, then the value of n is
A6B8C9D10A puck is moving in a circle in a circle of radius r0 with a constant speed v0 on a level frictionless table. A string is attached to the punk, which holds it in the circle, the string passes through a frictionless hole and is attached on the other end to a hanging object of mass M. The puck is mow made to move with a speed v'=3v0, but still in circle. The mass of the hanging object is left unchanged. The acceleration a' of the punk and the radius r' of the circle are now given by
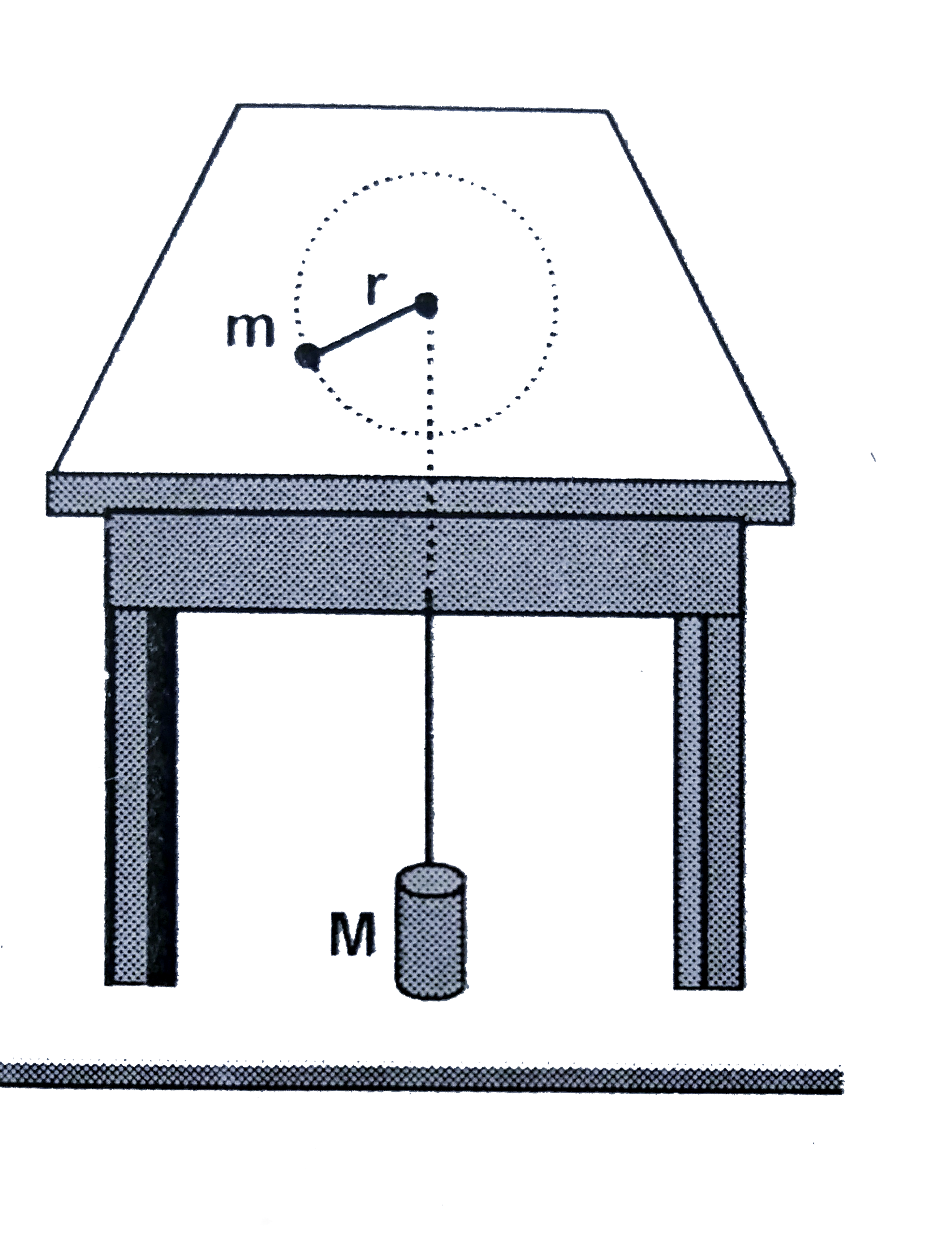 Aa'=9a0 and r'=r0Ba'=a0 and r'=9r0Ca'=9a0 and r'=9r0Da'=a0 and r'=r0
Aa'=9a0 and r'=r0Ba'=a0 and r'=9r0Ca'=9a0 and r'=9r0Da'=a0 and r'=r0A thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
Aω(M−2m)M+2mBωMM+2mCω(M+2m)MDωMM+m
A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0, The mass is attached to a string which passes through a smooth hole in the plane as shown.
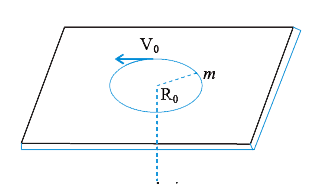
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy is :
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionA rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v0 hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.

View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to a string which passes through a smooth hole in the plane as shown.
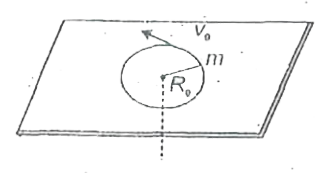
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy is
View Solution
