In the figure masses m1,m2 and M are kg. 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.

(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
The correct Answer is:(##ALNNCPHYNLMFE02008_A01##)
(ii) a=3/5m/s2,T=18N,F=60N
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (O-1)
51 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (O-2)
31 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-1)
26 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
In the figure masses m1,m2 and M are kg. 20 Kg, 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.

(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
View SolutionIn the figure masses m1,m2andM are 20 kg, 5 kg and 50 kg, respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1andM and that between m2 and ground is 0.3. The pulleys and the string are massless.
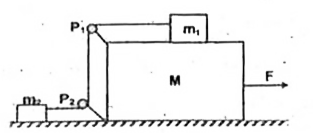
The string is perfectly horizontal between P1 and m1 and also between P2andm2. The string is perfectly vertical between P1andP2. An external horizontal force F is applied to the mass M. Take g=10m/s2.
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1andM be f1 and that between m2 and ground be f2. For a particular F, it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
View Solution
Knowledge Check
In the co-efficinet of friction between the floor and the body B is 0.1. The co-efficient of friction beteen the bodies B and A is 0.2 A fore F is applied as shown B The mass of A is m/2 and of B is m Which of the following statements are ture ?
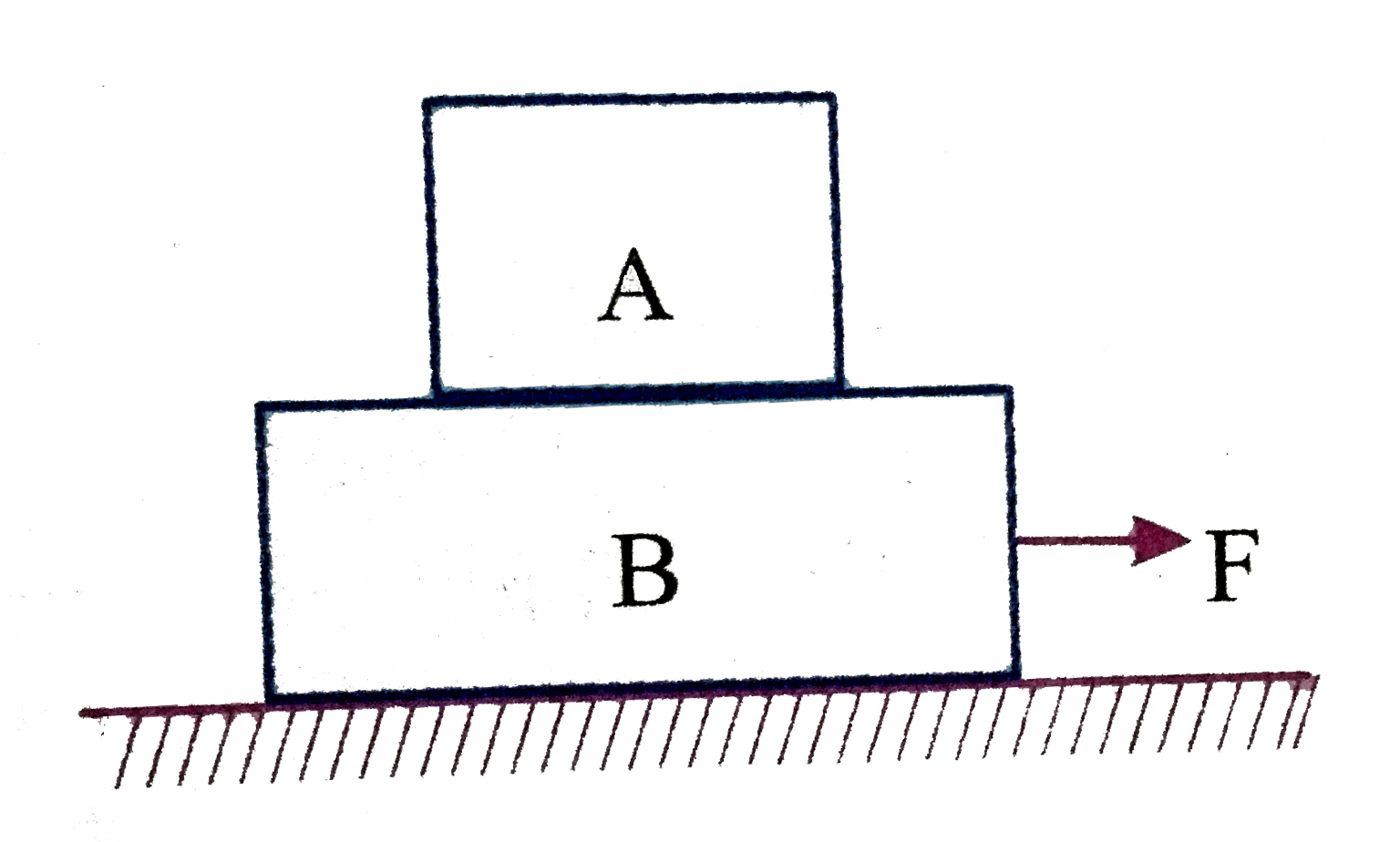 .AThe bodies will move together if F=0.25mgBThe body A will slip with respect to B if F=0.5mgCThe bodies will be at rest if F=0.5mgDThe maximum value of F for which the two bodies will move together is 0.45mg
.AThe bodies will move together if F=0.25mgBThe body A will slip with respect to B if F=0.5mgCThe bodies will be at rest if F=0.5mgDThe maximum value of F for which the two bodies will move together is 0.45mgIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the stringA1207NB2407NC1307NDNone of theseIn the figure shown m1=5kg,m2=10kg & friction coefficient between m1&m2 is μ=0.1 and ground is frictionless then :
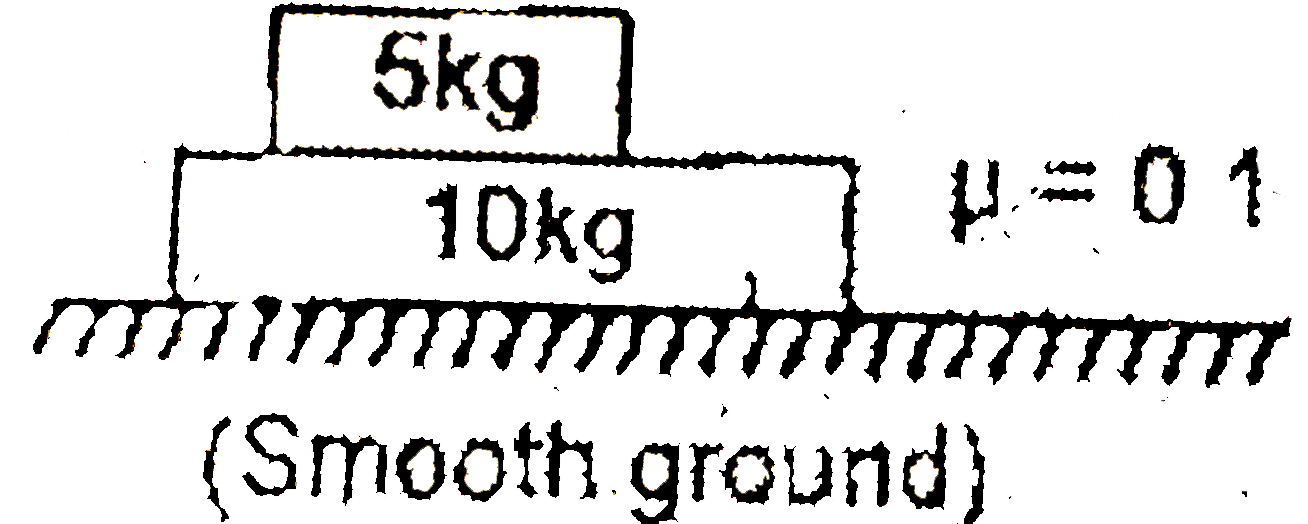 AIf a horizontal force F=20N is applied on m1 then the friction force acting on m2 is 5 N in the direction of FBMaximum amount of horizontal force that can be applied to m2 such that there is no relative motion between blocks is 15 NCIf a horizontal force F=20N is applied on m2 then friction force acting on m1 is 20/3 N in the direction of applied forceDMaximum amount of horizontal force that can be applied to m1 such that there is no relative motion between blocks is 8 N
AIf a horizontal force F=20N is applied on m1 then the friction force acting on m2 is 5 N in the direction of FBMaximum amount of horizontal force that can be applied to m2 such that there is no relative motion between blocks is 15 NCIf a horizontal force F=20N is applied on m2 then friction force acting on m1 is 20/3 N in the direction of applied forceDMaximum amount of horizontal force that can be applied to m1 such that there is no relative motion between blocks is 8 N
In the figure , masses m1,m2 and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between m1 and M and that between m2 and ground is0.4 . The pulleys and the string are massless . The string is perfectly horizontal between P1 and m1 and also between P2 and m2 . The string is perfectly vertical between P1 and P2 . An external horizonal force F is applied to the mass M . (Take g = 10m/s2)
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2 . For a particular F it is found that f1=2f2 . Find f1 and f2 . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .

View SolutionIn the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.

(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.
View SolutionIn the figure , masses m1,m2 and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between m1 and M and that between m2 and ground is0.4 . The pulleys and the string are massless . The string is perfectly horizontal between P1 and m1 and also between P2 and m2 . The string is perfectly vertical between P1 and P2 . An external horizonal force F is applied to the mass M . (Take g = 10m/s2)
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2 . For a particular F it is found that f1=2f2 . Find f1 and f2 . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .

View SolutionIn the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.

(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the string
View Solution
