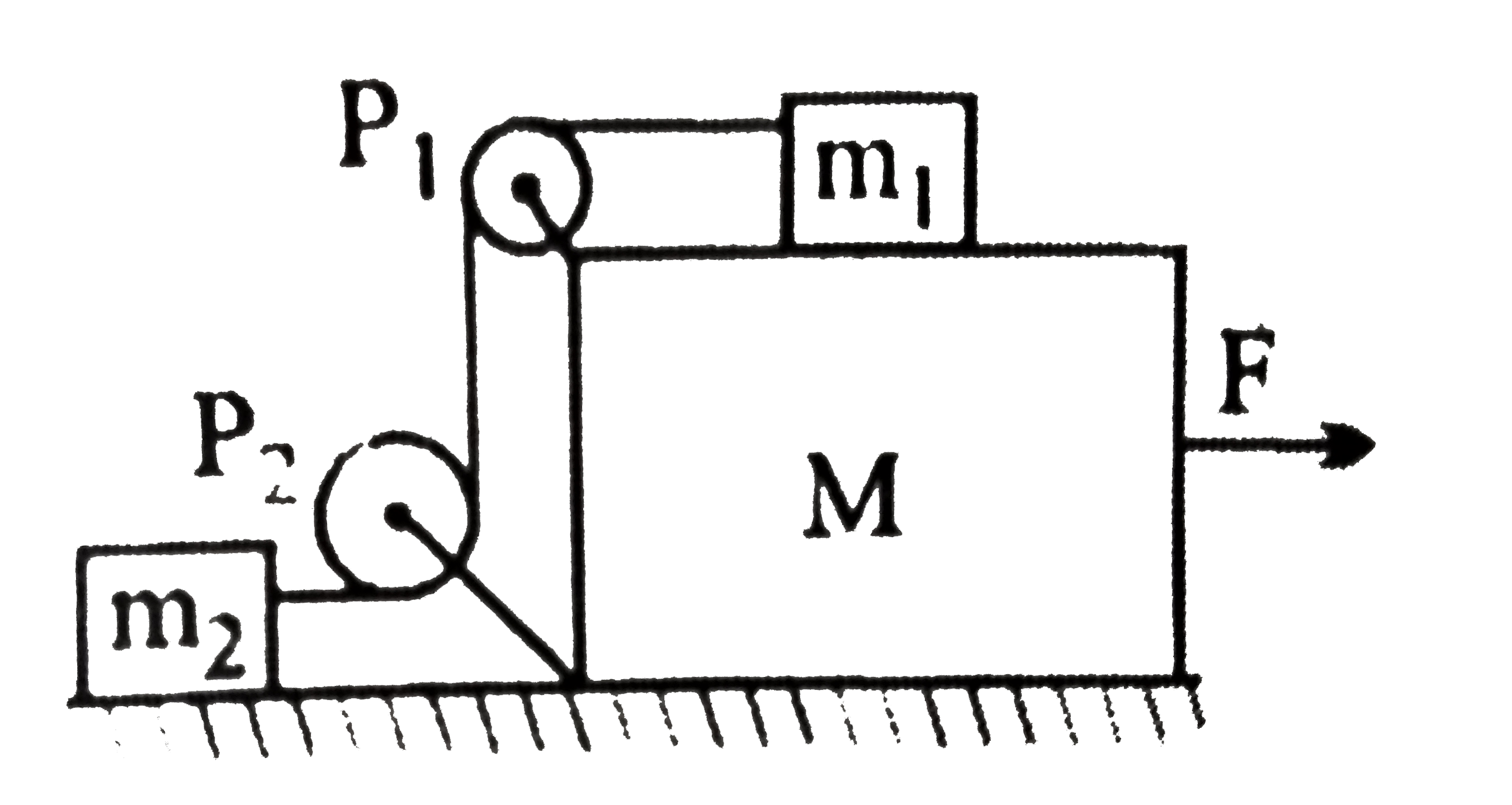
In the figure , masses m1,m2 and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between m1 and M and that between m2 and ground is0.4 . The pulleys and the string are massless . The string is perfectly horizontal between P1 and m1 and also between P2 and m2 . The string is perfectly vertical between P1 and P2 . An external horizonal force F is applied to the mass M . (Take g = 10m/s2)
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2 . For a particular F it is found that f1=2f2 . Find f1 and f2 . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .

The correct Answer is:A, B, C
Given m1=20kg, m2=5kg, M=50kg, μ=0.3 and g=10m/s2
(A) Free body diagram of mass M is
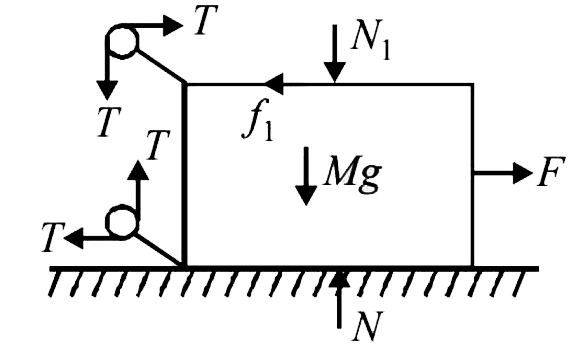
(B) The maximum value of f1 is
(f1)max=(0.3)(20)(10)=60N
The maximum value of f2 is
(f2)max=(0.3)(5)(10)=15N
Forces on m1 and m2 in horizontal direction are as follows:
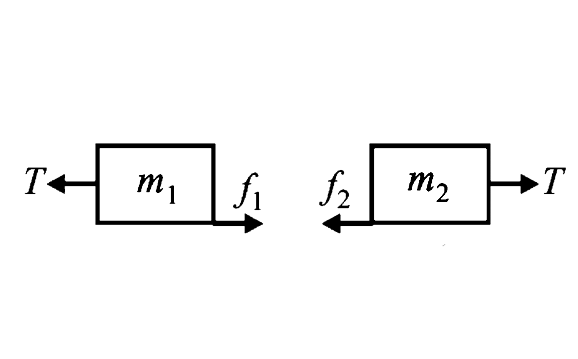
(1) Either both m1 and m2 will remain stationary (w.r.t. ground) or (2) both m1 and m2 will move (w.r.t. ground). First case is possible when.
T≤(f1)max or T≤60N
and T≤(f2)max or T≤15N
These conditions will be satisfied when T≤15N say T=14 then f1=f2=14N.
Therefore the condition f1=2f2 will not be satisfied.
Thus m1 and m2 both can't remain stationary.
In the second case, when m1 and m2 both move
f2=(f2)max=15N
Therefore, f1=2f2=30N
Free body diagrams and equations of motion are as follows:
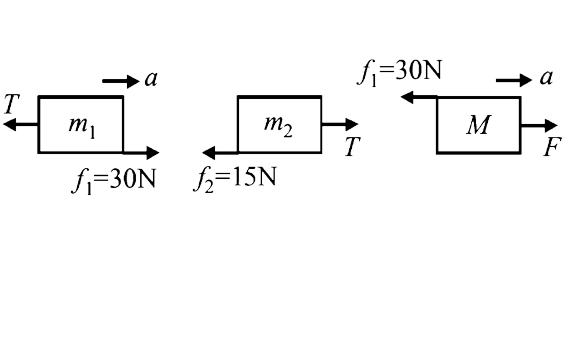
For m1:30−T=20a ...(i)
For m2:T−15=5a ...(ii)
For M:F−30=50a ...(iii)
Solving these three equations, we get,
F=60N, T=18N and a=35m/s2.
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219 Videos
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
Similar Questions
In the figure masses m1,m2andM are 20 kg, 5 kg and 50 kg, respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1andM and that between m2 and ground is 0.3. The pulleys and the string are massless.
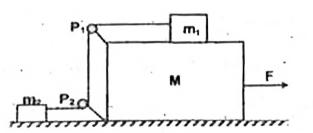
The string is perfectly horizontal between P1 and m1 and also between P2andm2. The string is perfectly vertical between P1andP2. An external horizontal force F is applied to the mass M. Take g=10m/s2.
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1andM be f1 and that between m2 and ground be f2. For a particular F, it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
View SolutionIn the figure masses m1,m2 and M are kg. 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.
(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
View Solution
Knowledge Check
The coefficient of friction between 4 kg and 5 kg blocks is 0.2 and between 5 kg block and ground is 0.1 respectively. Choose the correct statement : (Take g=10m/s2)
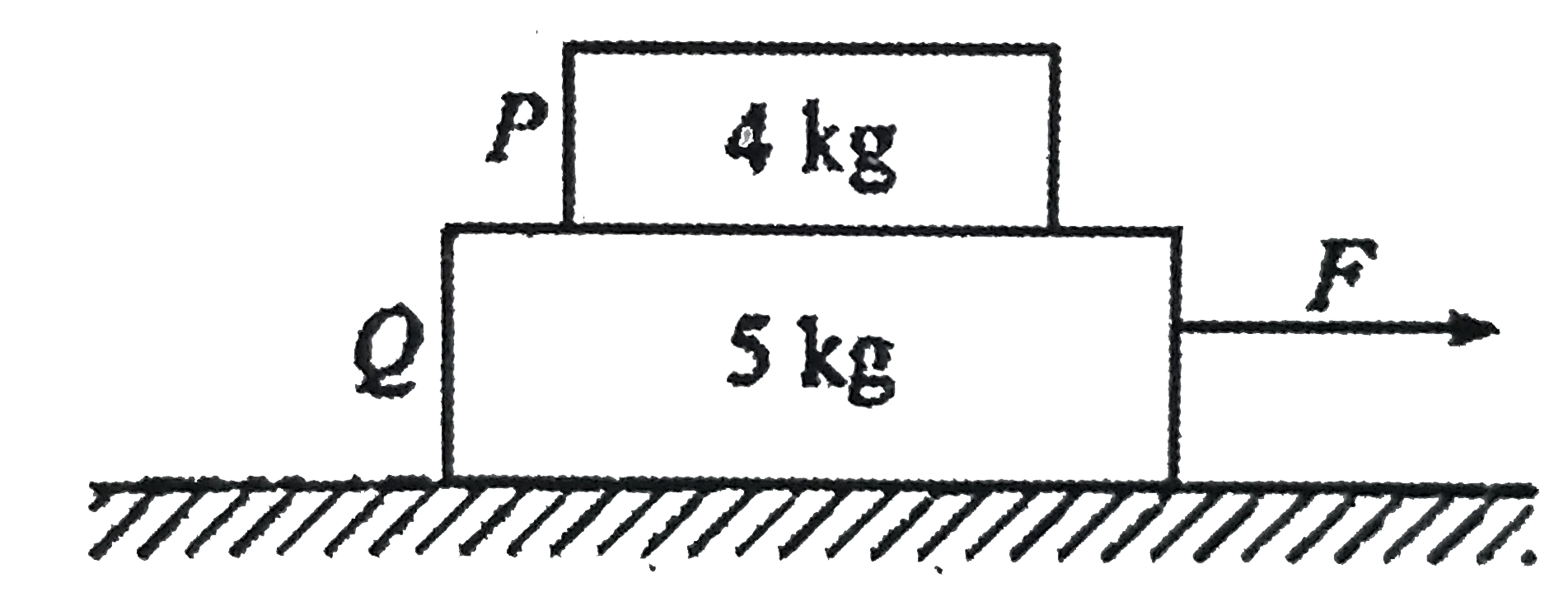 AMinimum force needed to cause system to move is 17 NBWhen force is 4 N static friction at all surfaces is 4 N to keep system at restCMaximum acceleration of 4 kg block is 2m/s2DSlipping between 4 kg and 5 kg blocks start when F is 17 N
AMinimum force needed to cause system to move is 17 NBWhen force is 4 N static friction at all surfaces is 4 N to keep system at restCMaximum acceleration of 4 kg block is 2m/s2DSlipping between 4 kg and 5 kg blocks start when F is 17 NIf, in Q.19, coefficient of friction between m1 and the wall is μ,and f1 and f2 are respectively, the force of friction on m1 and m2, then :
Af1 and f2 both are downward.Bf1 and f2 both are downward.Cf1 is upward and f2 upward.Df1 is downward and f2 upward.
In the figure , masses m1,m2 and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between m1 and M and that between m2 and ground is0.4 . The pulleys and the string are massless . The string is perfectly horizontal between P1 and m1 and also between P2 and m2 . The string is perfectly vertical between P1 and P2 . An external horizonal force F is applied to the mass M . (Take g = 10m/s2)
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2 . For a particular F it is found that f1=2f2 . Find f1 and f2 . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .

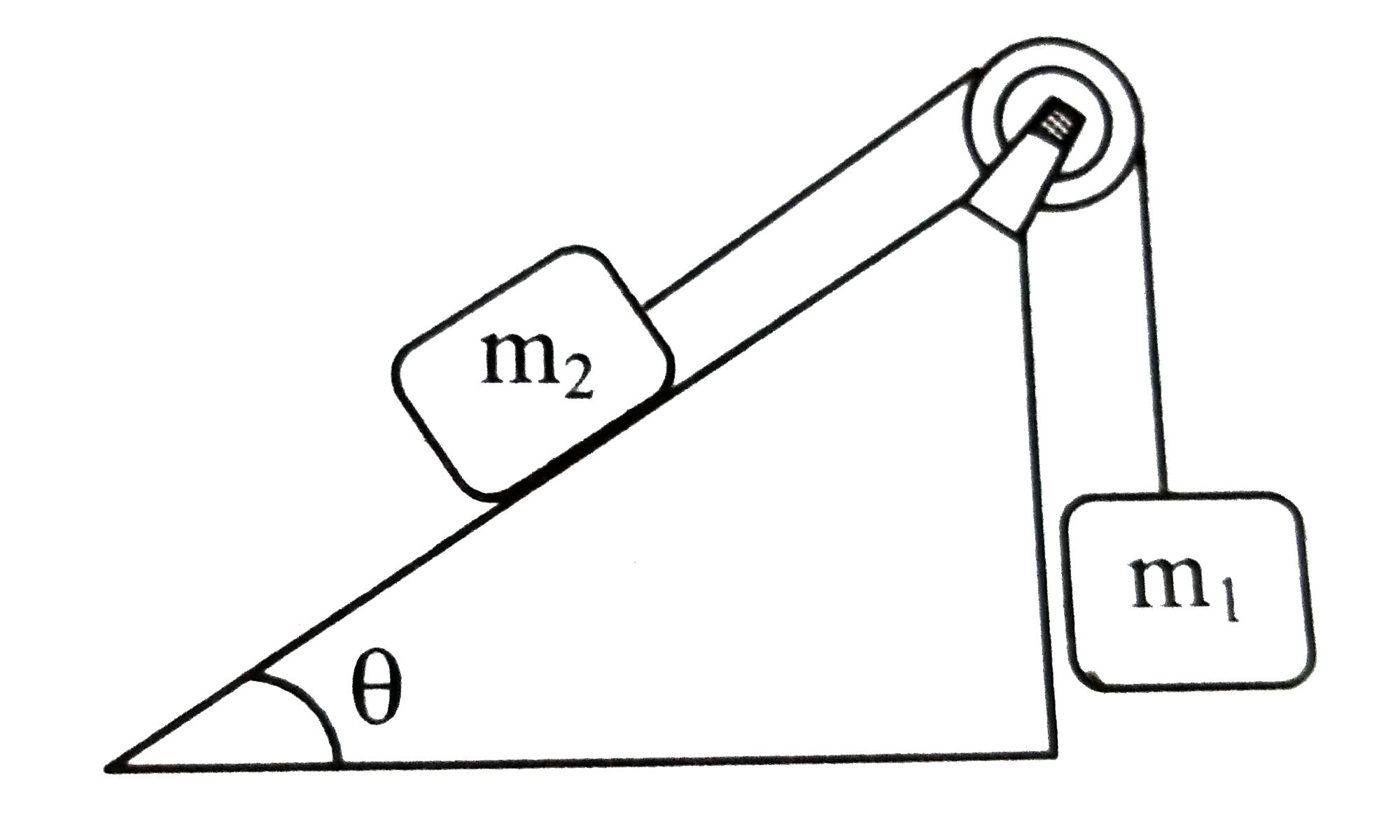
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View SolutionTwo blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



View SolutionWhen force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2

View SolutionWhen force F applied on m2 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ… What should be the minimum value of F so that there is no relative motion between m1andm2
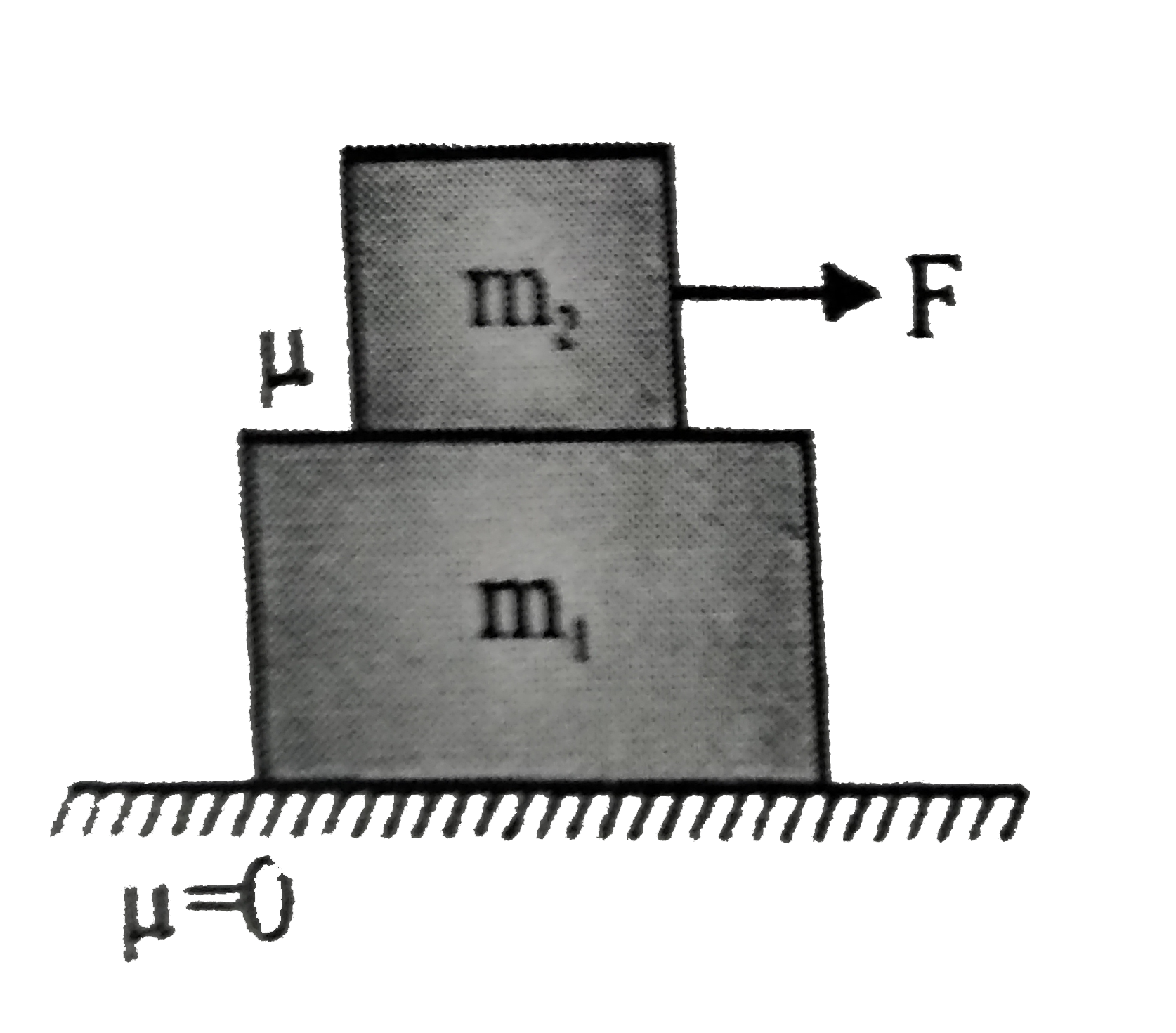
View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View Solution
