Keeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
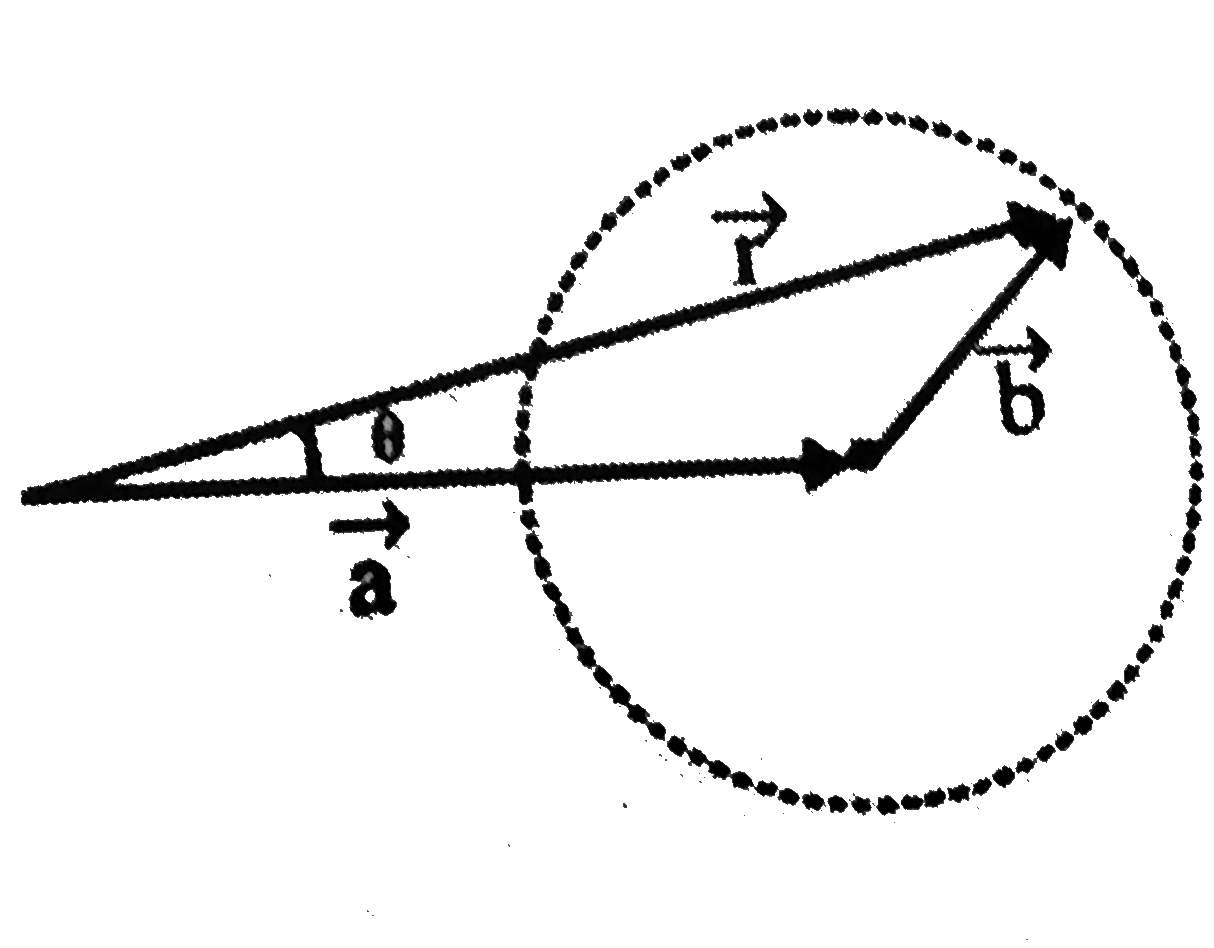
A
tan−1(br)
B
tan−1(b√a2−b2)
C
cos−1(r/a)
D
cos−1(a/r)
Video Solution
Text Solution
The correct Answer is:A, C
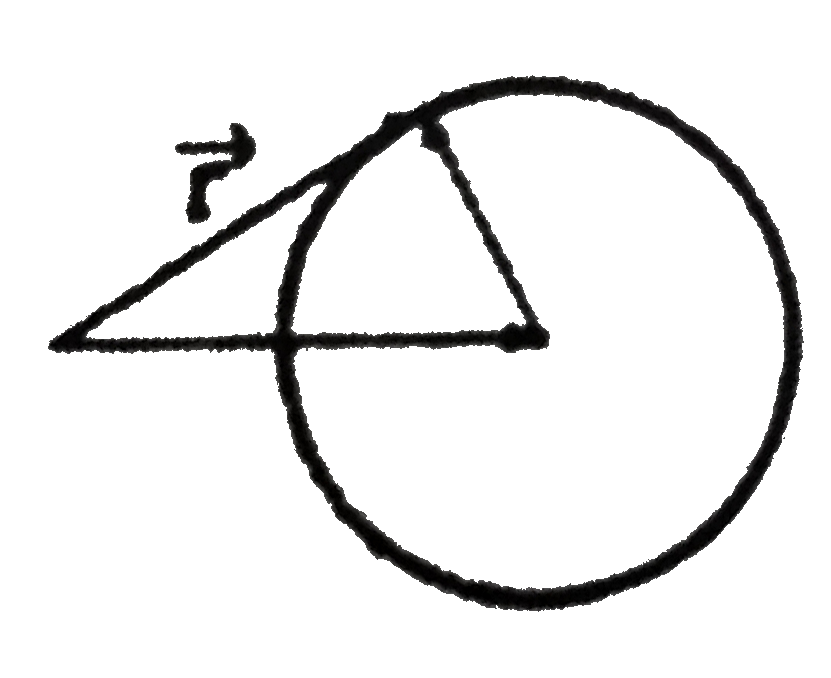 Angle between →r and →b is maximum when →r is tangent to circle.
Angle between →r and →b is maximum when →r is tangent to circle.
|
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (S-1)
Explore 22 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (S-2)
Explore 7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:MATHS
Explore 18 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 2 (Previous Year Questions)
Explore 7 Videos
Similar Questions
Knowledge Check
If →a.→b=∣∣→a×→b∣∣, then angle between vector →a and vector →b is :
Aπ2Bπ6Cπ4Dπ3If a vector →A is parallel to another vector →B then the resultant of the vector →A×→B will be equal to
AAB→ACZero vectorDZeroWhich one of the following is correct ? If the vector →c is normal to the vectors →aand→b, then →c, is :
Aparallel to both →a+→band→a−→bB→a−→band parallel to →a+→bCnormal to →a+→b and parallel to →a−→bDnormal to both →a+→band→a−→b
Find the angle between two vectors →a and →b, if ∣∣→a×→b∣∣=→a.→b .
View SolutionTwo vectors →Aand→B lie in plane, another vector →C lies outside this plane, then the resultant of these three vectors i.e., →A+→B+→C
View SolutionThe vector →a lies in the plane of vectors →band→c. Which one of the following is correct ?
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
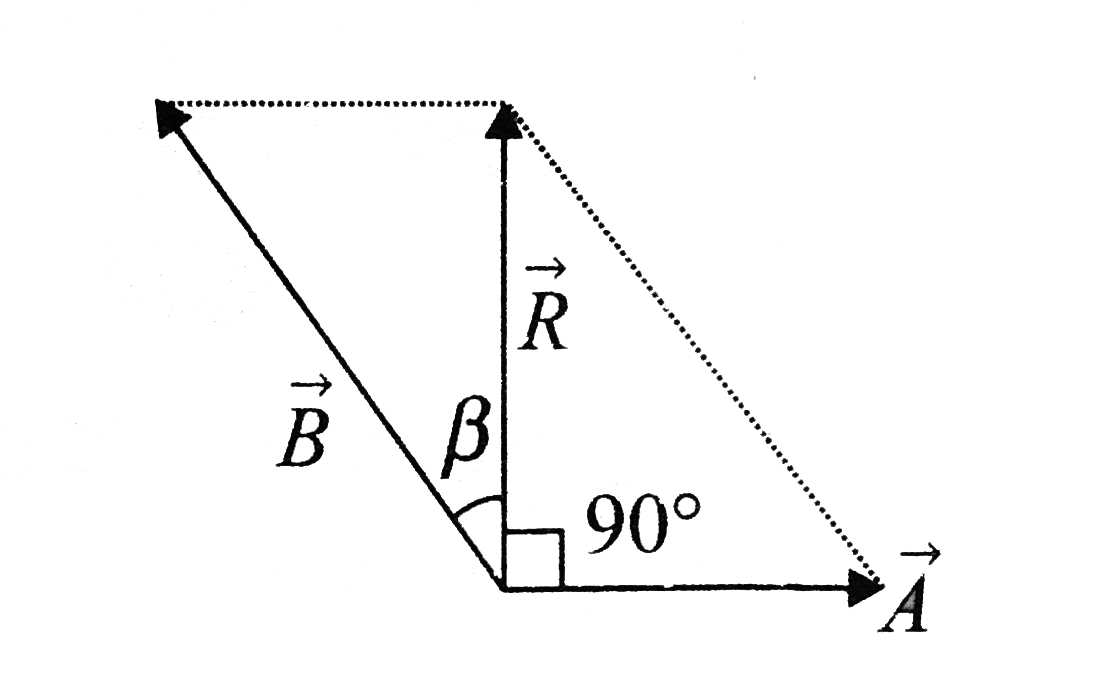
View SolutionIf for two vectors →A and →B,→A×→B=0, the vectors
View Solution
