A 16 ohm resistance wire is bent to form a square. A source of emf 9 volt is connected across one of its sides. Calculate the potential difference across any one of its diagonals.
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
Step 1: Understand the Setup
We have a wire with a total resistance of 16 ohms that is bent to form a square. The wire is connected to a 9-volt battery across one of its sides.
Step 2: Calculate the Resistance of Each Side of the Square
Since the wire is bent into a square, each side of the square will have an equal length. The total length of the wire is divided into four equal parts.
- Total resistance of the wire, Rtotal=16Ω
- Each side of the square, Lside=L4
- The resistance of each side, Rside=Rtotal4=16Ω4=4Ω
Step 3: Identify Points and Assign Potentials
Label the corners of the square as A, B, C, and D. The battery is connected across side DC. We will assign potentials as follows:
- Let the potential at point C be VC=0V (ground reference).
- The potential at point D will be VD=9V (since it is connected to the positive terminal of the battery).
Step 4: Apply Kirchhoff's Voltage Law (KVL)
To find the potential at point A, we will apply KVL to the loop that includes points D, A, B, and C.
1. The current flowing through the side CD is I1.
2. The current flowing through the side AB is I2.
Using KVL in the loop D → A → B → C → D:
VD−I1⋅RAB−VC=0
Where RAB=4Ω.
Step 5: Calculate Current I1
The total resistance in the loop is the sum of the resistances of the sides:
Rtotal_loop=RCD+RDA+RAB+RBC=4Ω+4Ω+4Ω+4Ω=16Ω
The current I1 through the loop can be calculated using Ohm's law:
I1=VRtotal_loop=9V16Ω=916A
Step 6: Calculate the Potential at Point A
Now, we can find the potential at point A using the current I1:
VA=VD−I1⋅RDA
Substituting the values:
VA=9V−(916A⋅4Ω)
VA=9V−3616V=9V−2.25V=6.75V
Step 7: Calculate the Potential Difference Across Diagonal AC
The potential difference across diagonal AC is given by:
VAC=VA−VC=6.75V−0V=6.75V
Final Answer
The potential difference across diagonal AC is 6.75V.
We have a wire with a total resistance of 16 ohms that is bent to form a square. The wire is connected to a 9-volt battery across one of its sides.
Since the wire is bent into a square, each side of the square will have an equal length. The total length of the wire is divided into four equal parts.
- Each side of the square, Lside=L4
- The resistance of each side, Rside=Rtotal4=16Ω4=4Ω
Label the corners of the square as A, B, C, and D. The battery is connected across side DC. We will assign potentials as follows:
- Let the potential at point C be VC=0V (ground reference).
- The potential at point D will be VD=9V (since it is connected to the positive terminal of the battery).
To find the potential at point A, we will apply KVL to the loop that includes points D, A, B, and C.
2. The current flowing through the side AB is I2.
VD−I1⋅RAB−VC=0
Where RAB=4Ω.
The total resistance in the loop is the sum of the resistances of the sides:
Rtotal_loop=RCD+RDA+RAB+RBC=4Ω+4Ω+4Ω+4Ω=16Ω
The current I1 through the loop can be calculated using Ohm's law:
I1=VRtotal_loop=9V16Ω=916A
Now, we can find the potential at point A using the current I1:
VA=VD−I1⋅RDA
Substituting the values:
VA=9V−(916A⋅4Ω)
VA=9V−3616V=9V−2.25V=6.75V
The potential difference across diagonal AC is given by:
VAC=VA−VC=6.75V−0V=6.75V
The potential difference across diagonal AC is 6.75V.
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS
6 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
A 16Ω wire is bend to form a square loop. A 9 V supply having internal resistance of 1Ω is connected across one of its sides. The potential drop across the diagonals of the square loop is _______×10−1V
View SolutionA square loop of total resistance 16 ohm. If a battery of 2V and 1ohm internal resistance is connected across one of its side then find potential difference across its diagnol
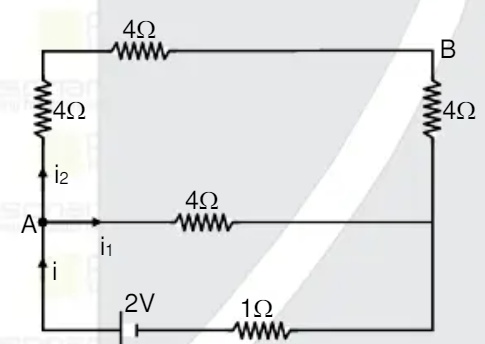
View Solution
Knowledge Check
A uniform wire of resistance 12Ω is bent in the form of a square. A cell of emf6V having negligible innternal resistance connected across the diagonal of the square. The magnetic induction at its centre ( in tesla ).
A0B10−7C5×10−7Dμ04π×5×10−7n identical cells, each of emf ε and internal resistance r, are joined in series to form a closed circuit. One cell A is joined with reversed polarity. The potential difference across any one cell is
AzeroBεCεnDn−1nεn identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
AE/nBE/nrCnE/rD0
Can the potential difference across a battery be greater than its emf?
View SolutionIf a current of 3 A flows through a wire of resistance 8 ohms, calculate the potential difference applied across its ends.
View SolutionWrite the relation between electric power of a devices with potential difference across its two ends and its resistance .
View SolutionA wire is bent to form a square of side 22 cm. If the wire is rebent to form a circle, its radius is
View SolutionA capacitor of capacitance 5 μF is charged to a potential difference of 10 volts and another capacitor of capacitance 9 μF is charged to a potential difference of 8 volts. Now these two capacitors are connected in such a manner that the positive plate of one is connected to the positive plate of other. Calculate the common potential difference across the two capacitors.
View Solution
