Question

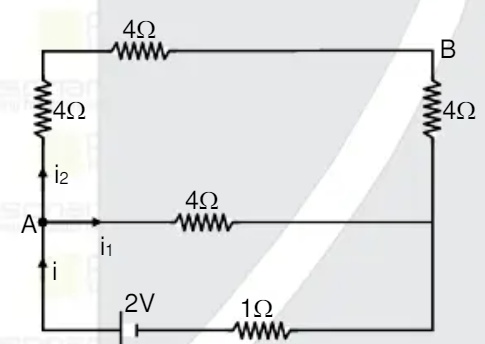
A $16\Omega$ wire is bend to form a square loop. A 9 V supply having internal resistance of $1\Omega$ is connected across one of its sides. The potential drop across the diagonals of the square loop is $\text{\_\_\_\_\_\_\_}\times {10}^{-1}V$

Explanation

To solve the problem, we need to find the potential drop across the diagonals of a square loop formed by a wire of resistance $$16\Omega$$ when connected to a $$9V$$ supply with an internal resistance of $$1\Omega$$.

1. Determine the Resistance of One Side of the Square Loop:
The total resistance of the wire is \(16 \, \Omega\). Since the wire is bent into a square loop, each side of the square will have a resistance of:
\( R_{\text{side}} = \frac{16 \, \Omega}{4} = 4 \, \Omega \)

2. Identify the Circuit Configuration:
The \(9 \, V\) battery with an internal resistance of \(1 \, \Omega\) is connected across one side of the square loop. This means that the side connected to the battery has a resistance of \(4 \, \Omega\) and the other three sides (which are not connected to the battery) have a combined resistance of \(12 \, \Omega\) (since \(4 \, \Omega \times 3 = 12 \, \Omega\)).

3. Calculate the Total Resistance in the Circuit:
The total resistance in the circuit can be calculated as follows:
- The \(1 \, \Omega\) internal resistance of the battery is in series with the equivalent resistance of the loop.
- The three sides of the loop (12 ohms) and the side connected to the battery (4 ohms) can be treated as follows:
\( R_{\text{total}} = R_{\text{internal}} + R_{\text{loop}} = 1 \, \Omega + 12 \, \Omega \parallel 4 \, \Omega \)
To find the equivalent resistance of \(12 \, \Omega\) and \(4 \, \Omega\) in parallel:
\( R_{\text{parallel}} = \frac{12 \times 4}{12 + 4} = \frac{48}{16} = 3 \, \Omega \)
Therefore, the total resistance is:
\( R_{\text{total}} = 1 \, \Omega + 3 \, \Omega = 4 \, \Omega \)

4. Calculate the Total Current in the Circuit:
Using Ohm's law, the total current \(I\) can be calculated as:
\( I = \frac{V}{R_{\text{total}}} = \frac{9 \, V}{4 \, \Omega} = \frac{9}{4} \, A \)

5. Determine the Voltage Drop Across the Loop:
The voltage drop across the loop can be calculated as:
\( V_{\text{loop}} = V - I \cdot R_{\text{internal}} = 9 \, V - \left(\frac{9}{4} \times 1 \, \Omega\right) = 9 \, V - \frac{9}{4} \, V = \frac{27}{4} \, V \)

6. Calculate the Current Through the Loop:
The current \(I_1\) flowing through the three sides of the loop (12 ohms) can be calculated as:
\( I_1 = \frac{V_{\text{loop}}}{12 \, \Omega} = \frac{\frac{27}{4}}{12} = \frac{27}{48} \, A \)

7. Calculate the Potential Drop Across the Diagonal:
The potential drop across the diagonal \(AB\) can be calculated as:
\( V_{AB} = I_1 \cdot R_{\text{diagonal}} = I_1 \cdot 8 \, \Omega \)
where \(R_{\text{diagonal}} = 4 \, \Omega + 4 \, \Omega = 8 \, \Omega\):
\( V_{AB} = \left(\frac{27}{48}\right) \cdot 8 = \frac{27 \cdot 8}{48} = \frac{216}{48} = \frac{27}{6} = 4.5 \, V \)

8. Express the Answer in the Required Format:
The potential drop across the diagonals of the square loop is:
\( V_{AB} = 4.5 \, V = 45 \times 10^{-1} \, V \)

Final Answer:
The potential drop across the diagonals of the square loop is \(45 \times 10^{-1} \, V\).