Show that the decay rate R of a sample of radionuclide is related to the number of radioactive nuclei N at the same instant by the expression R=λN.
N=N0e−λt differentiating both sides we get dNdt=−λN0e−λt=−λN i.e, decay rate
R=−dNdt=λN
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIEXERCISE - VERY SHORT ANSWER QUESTIONS (3 mark)22videos
DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEI
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIEXERCISE - LONG ANSWER QUESTIONS (5 MARKS)3videos
DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEI
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIEXERCISE - VERY SHORT ANSWER QUESTIONS (1 mark)10videos
DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEI
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)EXERCISE - SECTION E6videos
CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROMAGNETIC WAVES AND OPTICSEXERCISE - 1 mark question11videos
ELECTROMAGNETIC WAVES AND OPTICS
Similar Questions
Show that the decay rate R of a sample of radionuclide is related to the number of radioactive nuclei N at the same instant by the expression R=λN.
View SolutionThe rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively
and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
Rate of accumulation of B of any instant will beView Solution
Knowledge Check
- Question 1 - Select One
The rate at which a particular decay process occurs in a radio active sample, is proportional to the number of radio active nuclei present. If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN.
_E01_161_Q01.png)
Consider radioavtive decay of A to B which may further decay, either to X or to Y, λ1,λ2 and λ3 are decay constants for A to B decay, B to X decay and B of Y decay respectively. If at t=0 number of nuclei of A, B, X and Y are N0,N0, zero and zero respectively and N1,N2,N3,N4 are number of nuclei A,B,X and Y at any intant.
At t=∞, which of the following is incorrect ?AN2=0BN3=N0λ2λ2+λ3CN4=2N0λ3λ2+λ3DN3+N4+N1+N2=2N0 - Question 2 - Select One
In a sample of radioactive material, what percentage of the initial number of active nuclei will decay during one mean life ?
A69.3%B0.63C0.5D0.37 - Question 3 - Select One
For a radioactive sample, at given instant, number of active nuclei is N and its decay constant is λ then the incorrect relation is–
ANλ = activity at given instantBλ= decay probability per unit time of nucleusCAfter the next 1λ time interval active nuclei in the sample will be N(1−1e)DThe half life of the sample =ln2λ
The rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively
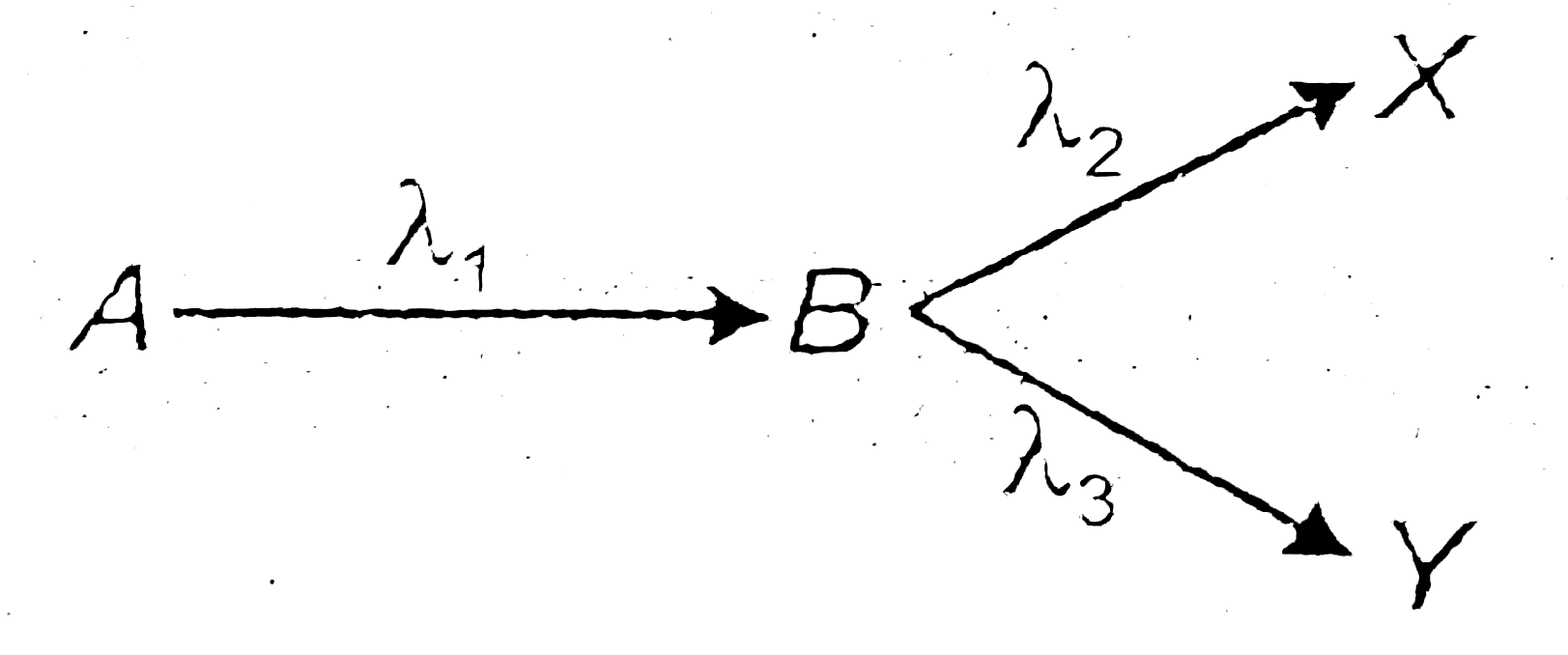
and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
The number of nuclei of B will first increase then after a maximum value, it will decreases, ifView SolutionThe rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively
and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
At t=∞, which of the following is incorrect ?View SolutionDraw a graph showing the variation of decay rate with number of active nuclei.
View SolutionDraw a graph showing the variation of decay rate with number of active nuclei.
View SolutionDraw a graph showing the variation of decay rate (−dNdt) with number (N) of radioactive nuclei.
View Solution