Two charges +8q and -2q are fixed on X-axis at origin and x=+a locations. A third charge +q is to be located on X-axis (other than infinitely far away) so that it is in equilibrium. The location of the third charge is correctly represented by
x=2a
x=3a/2
x=−a
x=3a
The correct Answer is:A
To find the position of the third charge +q such that it is in equilibrium, we can follow these steps:
Step 1: Understand the Configuration
We have two fixed charges:
- Charge 1: +8q at the origin (x = 0)
- Charge 2: -2q at x = +a
We need to place a third charge +q on the x-axis such that the net force acting on it is zero.
Step 2: Determine Possible Regions for Charge +q
Since +q is a positive charge, it will experience a repulsive force from +8q and an attractive force from -2q. We need to analyze the possible positions for +q:
1. To the left of +8q (x < 0)
2. Between +8q and -2q (0 < x < a)
3. To the right of -2q (x > a)
Step 3: Analyze Each Region
- Left of +8q (x < 0): The force from +8q will push +q to the right (repulsion), and the force from -2q will pull +q to the left (attraction). This will not lead to equilibrium as both forces will act in the same direction.
- Between +8q and -2q (0 < x < a): Here, +q will be repelled by +8q and attracted by -2q. The net force will not be zero as the repulsion will be stronger due to the proximity to +8q.
- Right of -2q (x > a): In this region, +q will be repelled by -2q and attracted by +8q. There is a possibility for equilibrium here.
Step 4: Set Up the Force Equations
Let’s assume the position of +q is at a distance r from the origin (x = 0). The distance from +8q to +q is r, and the distance from -2q to +q is (r - a).
The forces acting on +q due to +8q and -2q can be expressed as:
- Force due to +8q (F1):
F1=k⋅8q⋅qr2
- Force due to -2q (F2):
F2=k⋅2q⋅q(r−a)2
Step 5: Set the Forces Equal for Equilibrium
For equilibrium, the magnitudes of the forces must be equal:
F1=F2
This gives us:
k⋅8q2r2=k⋅2q2(r−a)2
Cancelling out common terms (k and q^2):
8r2=2(r−a)2
Step 6: Cross Multiply and Solve
Cross multiplying gives:
8(r−a)2=2r2
Expanding and simplifying:
8(r2−2ar+a2)=2r2
8r2−16ar+8a2=2r2
6r2−16ar+8a2=0
Step 7: Solve the Quadratic Equation
Using the quadratic formula r=−b±√b2−4ac2a:
Here, a=6,b=−16a,c=8a2:
r=16a±√(−16a)2−4⋅6⋅8a22⋅6
r=16a±√256a2−192a212
r=16a±√64a212
r=16a±8a12
This gives two solutions:
1. r=24a12=2a
2. r=8a12=2a3 (not valid as it is between the two charges)
Conclusion
The only valid position for the charge +q in equilibrium is at r=2a.
Thus, the location of the third charge is correctly represented by 2a.
---
We have two fixed charges:
- Charge 1: +8q at the origin (x = 0)
- Charge 2: -2q at x = +a
Since +q is a positive charge, it will experience a repulsive force from +8q and an attractive force from -2q. We need to analyze the possible positions for +q:
1. To the left of +8q (x < 0)
2. Between +8q and -2q (0 < x < a)
3. To the right of -2q (x > a)
- Left of +8q (x < 0): The force from +8q will push +q to the right (repulsion), and the force from -2q will pull +q to the left (attraction). This will not lead to equilibrium as both forces will act in the same direction.
- Between +8q and -2q (0 < x < a): Here, +q will be repelled by +8q and attracted by -2q. The net force will not be zero as the repulsion will be stronger due to the proximity to +8q.
Let’s assume the position of +q is at a distance r from the origin (x = 0). The distance from +8q to +q is r, and the distance from -2q to +q is (r - a).
- Force due to +8q (F1):
F1=k⋅8q⋅qr2
- Force due to -2q (F2):
F2=k⋅2q⋅q(r−a)2
For equilibrium, the magnitudes of the forces must be equal:
F1=F2
This gives us:
k⋅8q2r2=k⋅2q2(r−a)2
Cancelling out common terms (k and q^2):
8r2=2(r−a)2
Cross multiplying gives:
8(r−a)2=2r2
Expanding and simplifying:
8(r2−2ar+a2)=2r2
8r2−16ar+8a2=2r2
6r2−16ar+8a2=0
Using the quadratic formula r=−b±√b2−4ac2a:
Here, a=6,b=−16a,c=8a2:
r=16a±√(−16a)2−4⋅6⋅8a22⋅6
r=16a±√256a2−192a212
r=16a±√64a212
r=16a±8a12
This gives two solutions:
1. r=24a12=2a
2. r=8a12=2a3 (not valid as it is between the two charges)
The only valid position for the charge +q in equilibrium is at r=2a.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -2 (C.W.)39videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -2 (H.W)36videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -1 (C.W)24videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (H.W)17videos
DUAL NATURE
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (H.W)23videos
ELECTRO MAGNETIC INDUCTION
Similar Questions
Two free charges q and 4q are placed at a distance d apart A third charge Q is placed between them at a distance x from charge q such that the system is in equilibrium. Then magnitude of third charge and postion,
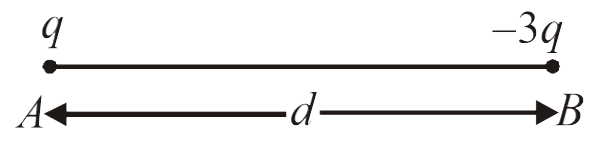
View SolutionTwo charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
AAt a distance L3 from +4q charge, 4q9BAt a distance L3 from +4q charge −4q9CAt a distance 2L3 from +4q charge −4q9DAt a distance 2L3 from +q charge 4q9 - Question 2 - Select One or More
Two force point charges +q and +4q are a distance l apart. A third charge q1 is so placed that the entire system is in equilibrium. Find the location, magnitude and sign of the third charge.
Aq1=49qBq1=−49qCq1 is to be placed at a distance l/3 from q.Dq1 is to be placed at a distance 2l3 from 4q. - Question 3 - Select One
Two point charges +q and −q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then
Auknknown charge is −4q/9Bunknown charge is −9q/4Cit should be at (x/3)from smaller chargge between themDnone of these
Two point electric charges of value q and 2q are kept at a distance d apart from each other in air. A third charge Q is to be kept along the same line in such a way that the net force action on q and 2q is zero. Calculate the position of charge Q in terms of q and d.
View SolutionTwo charges q and 3q are placed fixed on x-axis separated by distance 'd'. Where should a third charge 2q be placed such that it will not experience any force ?
View SolutionTwo charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?
 View Solution
View SolutionTwo free charges q and 4q are placed at a distance d apart A third charge Q is placed between them at a distance x from charge q such that the system is in equilibrium. Then
View SolutionTwo charges q and −3q are placed fixed on x-axis separated by distance d. Where should a third charge 2q be placed such that it will not experience any force ?
View Solution

