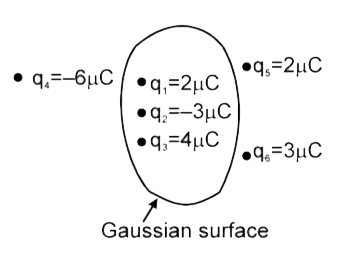
Calculate the net flux emergin from given enclosed surface $N m^{2} C^{- 1}$

A

$4.5 \times 10^{11}$

B

$45 \times 10^{12}$

C

zero

D

$1.12 \times 10^{12}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$\int ¯ ¯ ¯ E . ¯ ¯¯ ¯ d s = \frac{q}{ε_{0}} = \frac{2 + 5 - 3}{8.85 \times 10^{- 12}} = 4.5 \times 10^{11}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -2 (C.W.)
39videos
ELECTRIC CHARGES AND FIELDS
BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -2 (H.W)
36videos
ELECTRIC CHARGES AND FIELDS
BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -1 (C.W)
24videos
ELECTRIC CHARGES AND FIELDS
BOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (H.W)
17videos
DUAL NATURE
BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (H.W)
23videos
ELECTRO MAGNETIC INDUCTION

Similar Questions

Knowledge Check

Question 1 - Select One
If the electric flux entering and leaving an enclosed surface are $ϕ_{1} and ϕ_{2}$ respectively, then the electric charge present within the surface is
A $\frac{1}{\in_{0}} (ϕ_{1} + ϕ_{2})$
B $\frac{1}{\in_{0}} (ϕ_{2} - ϕ_{1})$
C $\in_{0} (ϕ_{1} + ϕ_{2})$
D $\in_{0} (ϕ_{2} - ϕ_{1})$
Question 2 - Select One
If the electric flux entering and leaving an enclosed surface respectively is $ϕ_{1}$ and $ϕ_{2}$ then the electric charge inside the surface will he
A $(ϕ + ϕ_{2}) ε_{0}$
B $(ϕ_{2} - ϕ_{1}) ε_{0}$
C $(ϕ_{1} - ϕ_{2}) ε_{0}$
D $(- ϕ_{1} - ϕ_{2}) ε_{0}$
Question 3 - Select One
If the electric flux entering and leaving an enclosed surface respectively is $ϕ_{1}$ and $ϕ_{2}$ , the electric charge inside the surface will be
A $\frac{ϕ_{3} - ϕ_{1}}{ε_{n}}$
B $\frac{ϕ_{2} + ϕ_{1}}{ε_{n}}$
C $(ϕ_{1} - ϕ_{3}) ε_{n}$
D $ε_{n} (ϕ_{2} - ϕ_{1})$

NARAYNA-ELECTRIC CHARGES AND FIELDS-EXERCISE -1 (H.W)

Home
Ask Doubt
Profile