A regular tetrhedron has four identical faces each an equilaterla triangle of side L. A charge +q is kept at one of the vertices. The magnitude of electric intensity due to this charge at thecentroid of the face opposite tio it is (k=1/4pe0)
2Kq3L2
3Kq2L2
3kqL2
4kq3L2
The correct Answer is:B
To solve the problem of finding the electric intensity at the centroid of the face opposite to the vertex where a charge +q is placed in a regular tetrahedron, we can follow these steps:
1. Understand the Geometry of the Tetrahedron:
- A regular tetrahedron has four vertices and four triangular faces. Each face is an equilateral triangle with side length L.
- Let the vertices be labeled as A,B,C, and O (where O is the vertex with charge +q).
2. Identify the Centroid of the Opposite Face:
- The opposite face to vertex O is triangle ABC. The centroid G of triangle ABC can be found using the formula for the centroid of a triangle, which is the average of the vertices' coordinates.
3. Calculate the Distance from Charge to Centroid:
- The distance from vertex O to the centroid G can be calculated using the Pythagorean theorem.
- The height h of the equilateral triangle ABC can be calculated as:
h=√32L
- The distance from the centroid to the base (the line segment connecting the midpoints of the triangle) is h3=L√36.
- The vertical distance from O to the plane of triangle ABC is L√3 (the height from vertex O to the centroid of triangle ABC).
4. Calculate the Total Distance from Charge to Centroid:
- The total distance r from charge +q at vertex O to the centroid G can be found using:
r=
⎷(L√3)2+(L√36)2
- Simplifying this gives:
r=√L23+L212=√4L212+L212=√5L212=L√52√3
5. Calculate the Electric Field Intensity:
- The electric field intensity E due to a point charge is given by:
E=k⋅qr2
- Substituting r:
E=k⋅q(L√52√3)2=k⋅q5L212=12k⋅q5L2
6. Final Result:
- The magnitude of the electric intensity at the centroid of the face opposite to the charge +q is:
E=12kq5L2
- A regular tetrahedron has four vertices and four triangular faces. Each face is an equilateral triangle with side length L.
- Let the vertices be labeled as A,B,C, and O (where O is the vertex with charge +q).
- The opposite face to vertex O is triangle ABC. The centroid G of triangle ABC can be found using the formula for the centroid of a triangle, which is the average of the vertices' coordinates.
- The distance from vertex O to the centroid G can be calculated using the Pythagorean theorem.
- The height h of the equilateral triangle ABC can be calculated as:
h=√32L
- The distance from the centroid to the base (the line segment connecting the midpoints of the triangle) is h3=L√36.
- The vertical distance from O to the plane of triangle ABC is L√3 (the height from vertex O to the centroid of triangle ABC).
- The total distance r from charge +q at vertex O to the centroid G can be found using:
r=
⎷(L√3)2+(L√36)2
- Simplifying this gives:
r=√L23+L212=√4L212+L212=√5L212=L√52√3
- The electric field intensity E due to a point charge is given by:
E=k⋅qr2
- Substituting r:
E=k⋅q(L√52√3)2=k⋅q5L212=12k⋅q5L2
- The magnitude of the electric intensity at the centroid of the face opposite to the charge +q is:
E=12kq5L2
Topper's Solved these Questions
Similar Questions
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View SolutionA pyramid has four faces, all of them being equilateral triangle of side a. A charge Q is placed at the centre of one of the faces. What is the flux of electric field emerging from any one of the other three faces of the pyramid?
View Solution
Knowledge Check
A regular pentagon has four charges each +q at four of its vertices. At the centre of the pentagon, a charge +q is kept. If the distance of a vertex from the center is a the magnitude of the net force acting on the charge at the center is
Aq24pe0a2BzeroC4q24pe0a2D2q24pe0a2Three identical spheres, each having a charge q and radius R. are kept in such a way that each touches the other two. The magnitude of the electric force on any sphere due to the other two is
A14πε0(qR)2B√34πε0(qR)2C√316πε0(qR)2D√516πε0(qR)2Three point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
A(√34πε0)(qa)2B(√24πε0)(qa)2C(√34πε0)(q2a)2D(√24πε0)(2qa)2
Three charges -q +q and +q are placed at the corner of the equilateral triangle of side a as shown in the figure.The net electric potential at the centroid of the triangle will be (k=(1)/(4 pi varepsilon_(0)))
View SolutionThe length of each side of a cubical closed surfce is l If charge q is situated on one of the vertices of the cube , the find the passing through shaded face of the cube.
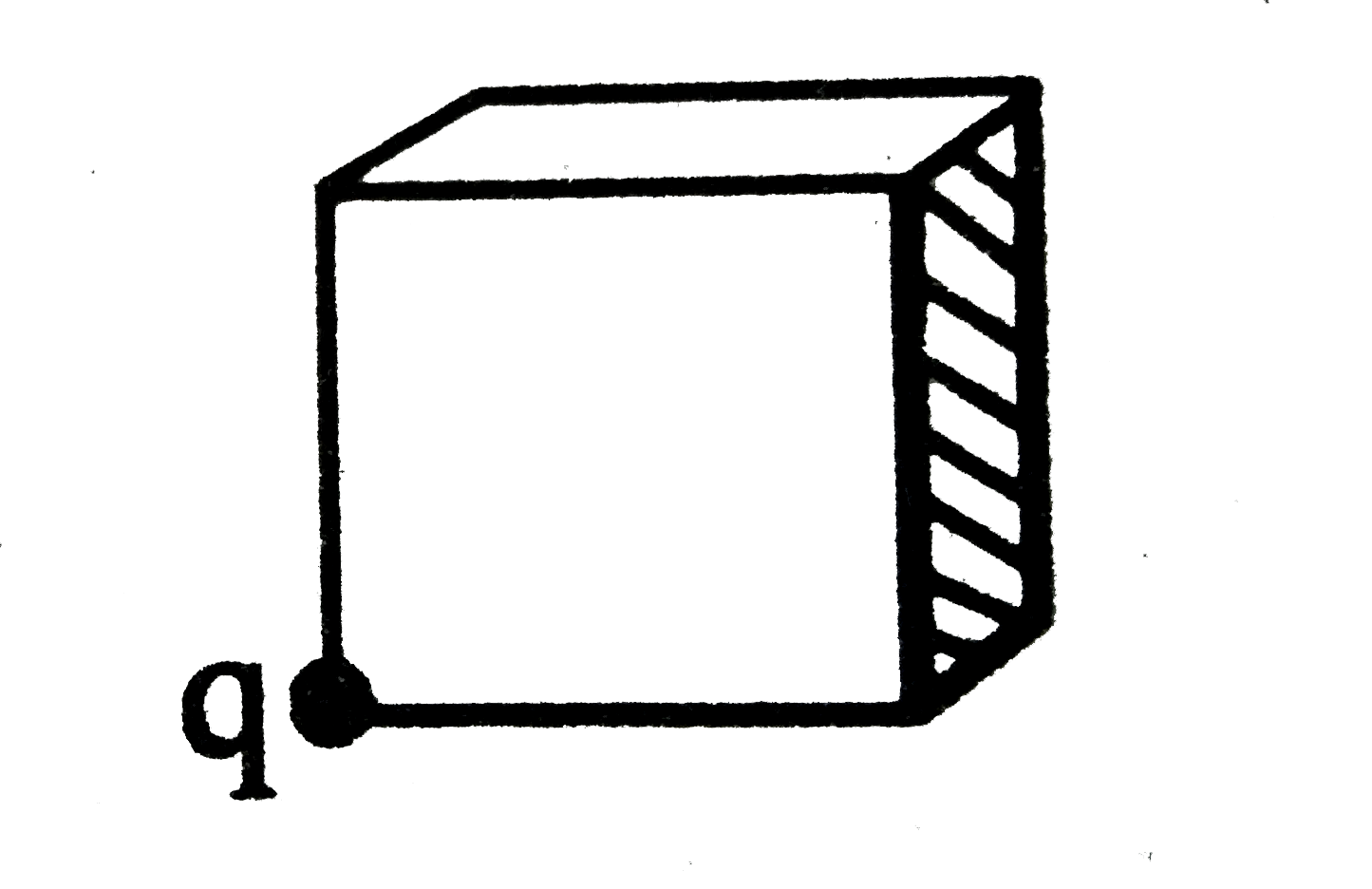 .
.
View SolutionFour identical charged particles of charge q are kept on the vertices of a cube with side 20 cm as shown in the figure. Calcualte the electric potential at point P in the centre of the cube due to all these charges.
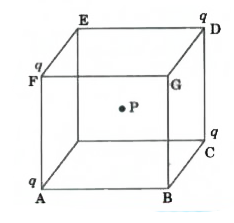
View SolutionConsider three charges q1,q2 and q3 each equal to q at the vertices of an equilateral triangle of side 'l' what is the force on any charge due to remaining charges.
View SolutionFour charges of same magnitude q are placed at four corners of a square of side a . The value electric potential at the centre of the square will be (where k = 14πε0 )
View Solution
