A uniform electrif field of intensit E is in the Y-negative direction. An electron of mass m and charge e is fired through the origin with initial velocity u in the X-positive direction. The displacement undergone of the electron during a time interval t is
ut
2Et2/2m
√ut+(eEt2/2m)2
√ut−(eEt2/2m)2
The correct Answer is:B
To solve the problem, we need to analyze the motion of the electron under the influence of the electric field. The electric field is directed in the negative y-direction, and the electron is fired with an initial velocity in the positive x-direction. We will calculate the displacement of the electron in both the x and y directions and then find the total displacement.
1. Identify the Forces Acting on the Electron:
- The electron has a charge e and is subjected to an electric field E in the negative y-direction.
- The force F on the electron due to the electric field is given by:
F=eE
- This force causes an acceleration ay in the y-direction, calculated using Newton's second law:
F=ma⟹ay=Fm=eEm
2. Analyze Motion in the X-Direction:
- The initial velocity in the x-direction is u.
- Since there is no force acting in the x-direction, the acceleration ax=0.
- The displacement in the x-direction Sx after time t is given by:
Sx=ut+12axt2=ut+12⋅0⋅t2=ut
3. Analyze Motion in the Y-Direction:
- The initial velocity in the y-direction uy=0 (since it is fired horizontally).
- The displacement in the y-direction Sy after time t is given by:
Sy=uyt+12ayt2=0+12(eEm)t2=eE2mt2
4. Calculate the Total Displacement:
- The total displacement S of the electron can be found using the Pythagorean theorem since the displacements in the x and y directions are perpendicular:
S=√S2x+S2y=√(ut)2+(eE2mt2)2
- Substituting the expressions for Sx and Sy:
S=√(ut)2+(eE2mt2)2
Final Answer:
The displacement undergone by the electron during the time interval t is:
S=√(ut)2+(eE2mt2)2
- The electron has a charge e and is subjected to an electric field E in the negative y-direction.
- The force F on the electron due to the electric field is given by:
F=eE
- This force causes an acceleration ay in the y-direction, calculated using Newton's second law:
F=ma⟹ay=Fm=eEm
- The initial velocity in the x-direction is u.
- Since there is no force acting in the x-direction, the acceleration ax=0.
- The displacement in the x-direction Sx after time t is given by:
Sx=ut+12axt2=ut+12⋅0⋅t2=ut
- The initial velocity in the y-direction uy=0 (since it is fired horizontally).
- The displacement in the y-direction Sy after time t is given by:
Sy=uyt+12ayt2=0+12(eEm)t2=eE2mt2
- The total displacement S of the electron can be found using the Pythagorean theorem since the displacements in the x and y directions are perpendicular:
S=√S2x+S2y=√(ut)2+(eE2mt2)2
- Substituting the expressions for Sx and Sy:
S=√(ut)2+(eE2mt2)2
The displacement undergone by the electron during the time interval t is:
S=√(ut)2+(eE2mt2)2
Topper's Solved these Questions
Similar Questions
An electron of mass ‘M’ kg and charge ‘e’ coulomb travels from rest through a potential difference of ‘V’ volt. The final velocity of the electron is (in m/s)
View SolutionLet there be a uniform electric field "E" existing along the positive X-direction.Assume electric potential to be zero at the origin.Potential at the point x=x0 is
View Solution
Knowledge Check
- Question 1 - Select One
In a region of space, a uniform magnetic field B exists in the x-direction. An electron is fired from the origin with its initial velocity u making an angle α with the y direction in the y-z plane. In the subsequent motion of the electron,
 Ay-coordinate of the electron will never be negativeBz-coordinate of the electron will never be negativeCx-coordinate of the electron will never be negativeDtrajectory of the electron would be helical
Ay-coordinate of the electron will never be negativeBz-coordinate of the electron will never be negativeCx-coordinate of the electron will never be negativeDtrajectory of the electron would be helical - Question 2 - Select One
A ball of mass 'm' is thrown at an angle is 'θ' with the horizontal with an initial velocity 'u'.The change in its momentum during its flight in a time interval of 't' is
AmgtBm>cosθCm>sinθD1/2m>. - Question 3 - Select One
An electron of mass m and charge e is accelerated from rest through a potential difference V in vacuum. The final speed of the electron will be
AV√e/mB√eV/mC√2eV/mD2eV/m
A uniform electric field of strength e exists in a region. An electron (charge -e, mass m) enters a point A with velocity Vˆj. It moves through the electric field & exits at point B. Then :
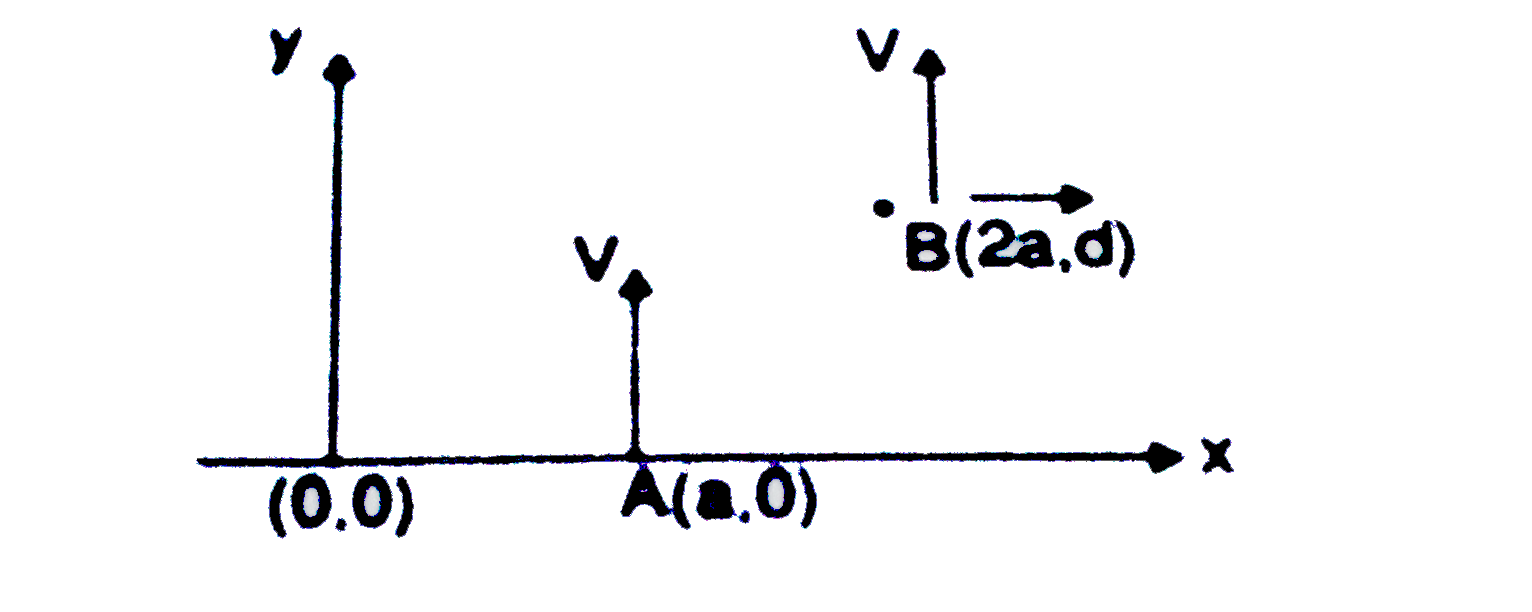 View Solution
View SolutionIn a region of space, a uniform magnetic field B exists in the y-direction A proton is fired from the origin, with its initial velocity v making a small angle alpha with the y-direction in the yz plane. In the subsequent motion of the proton
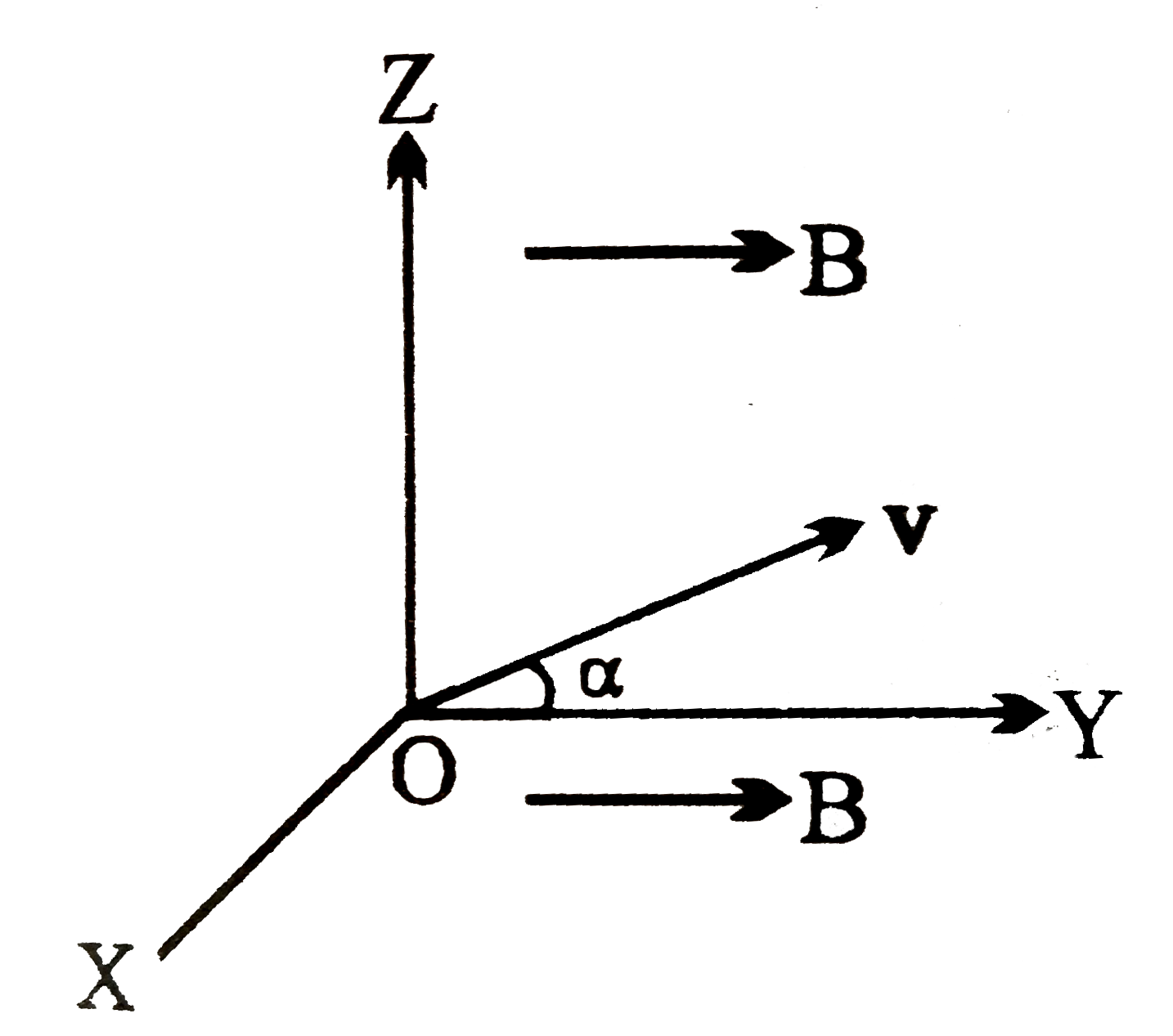 .View Solution
.View SolutionWhen an electron fo mass 6 m and charge 6e moves with a velocity of 7u about the nuclar charge Ze in a circular orbit fo radius r . The potential energy of the electron will be:
View SolutionAn electron moving with a uniform velocity along the positive x-direction enters a magnetic field directed along the positive y-direction. The force on the electron is directed along
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
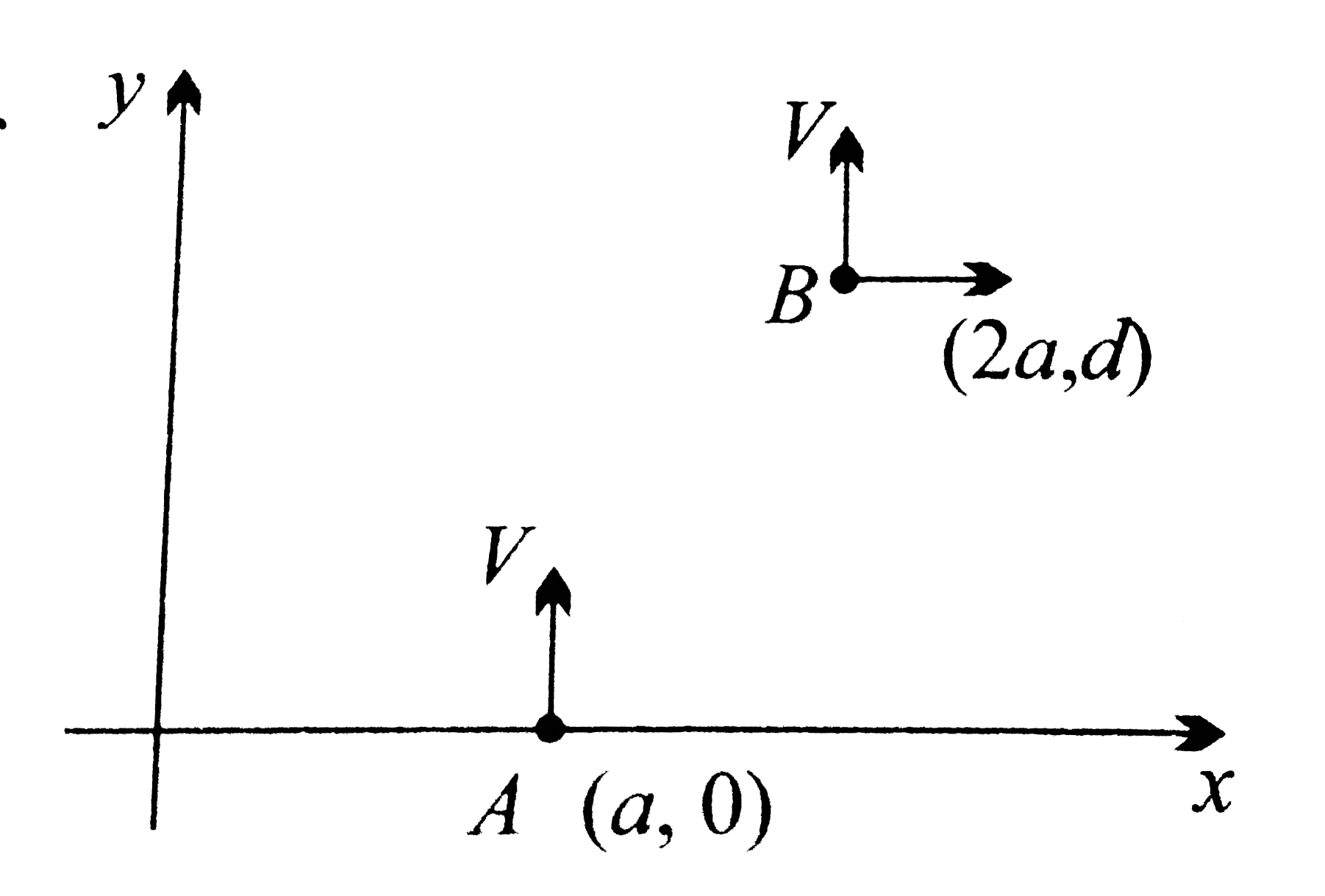 .
.
Find electric field.View Solution

