Two large conducting plates are placed parallel to each other with a separation of d between them. An electron starting from rest near one of the plates reaches the other plate in time t. If e is the charge on the electron and m is its mass, then the surface charge density on the inner surface is
dme4πε0t2
dmε04πet2
2dmε0et2
None of the above
The correct Answer is:C
To find the surface charge density on the inner surface of the two large conducting plates, we can follow these steps:
1. Understanding the Setup:
- We have two parallel conducting plates separated by a distance d.
- An electron starts from rest near one of the plates and reaches the other plate in time t.
2. Electric Field Between the Plates:
- The surface charge density on one plate is +σ and on the other plate is −σ.
- The electric field E between the plates is given by:
E=σϵ0
- Since there are two plates, the net electric field E is:
E=σϵ0
3. Force on the Electron:
- The force F acting on the electron due to the electric field is:
F=eE=e(σϵ0)
- The acceleration a of the electron can be calculated using Newton's second law:
a=Fm=eσmϵ0
4. Using the Equation of Motion:
- The electron travels a distance d in time t starting from rest. The equation of motion is:
d=ut+12at2
- Since the initial velocity u=0, we have:
d=12at2
- Substituting the expression for acceleration:
d=12(eσmϵ0)t2
5. Solving for Surface Charge Density σ:
- Rearranging the equation to solve for σ:
d=eσt22mϵ0
σ=2dmϵ0et2
Final Result:
The surface charge density on the inner surface of the plates is:
σ=2dmϵ0et2
- We have two parallel conducting plates separated by a distance d.
- An electron starts from rest near one of the plates and reaches the other plate in time t.
- The surface charge density on one plate is +σ and on the other plate is −σ.
- The electric field E between the plates is given by:
E=σϵ0
- Since there are two plates, the net electric field E is:
E=σϵ0
- The force F acting on the electron due to the electric field is:
F=eE=e(σϵ0)
- The acceleration a of the electron can be calculated using Newton's second law:
a=Fm=eσmϵ0
- The electron travels a distance d in time t starting from rest. The equation of motion is:
d=ut+12at2
- Since the initial velocity u=0, we have:
d=12at2
- Substituting the expression for acceleration:
d=12(eσmϵ0)t2
- Rearranging the equation to solve for σ:
d=eσt22mϵ0
σ=2dmϵ0et2
The surface charge density on the inner surface of the plates is:
σ=2dmϵ0et2
Topper's Solved these Questions
Similar Questions
Two large conducting plates are placed parallel to each other with a separation d. An electron (−e,m) starting from rest near one of the plates reaches the other plate in time t0. Find the surface density on the inner surface.
View SolutionTwo large conducting plates are placed parallel to each other with a separation of 2.00 cm betweeen them. An electron starting from rest near one of the plates reaches the other plate in 2.00 microseconds. Find the surface charge density on the inner surfaces.
View Solution
Knowledge Check
- Question 1 - Select One
Two large parallel conducting plates are placed close to each other ,the inner surface of the two plates have surface charge densities +σ and −σ .The outer surfaces are without charge.The electric field has a magnitude of
Aσε0 in the region between the platesBσε0 in the region outside the plates.C2σε0 in the region between the platesDzero in the region outside the plates. - Question 2 - Select One
Two plates, each of area A, are placed parallel to each other at a distance d. One plate is connected to a battery of emf E and its negative is earthed. The other plate is also earthed. The charge drawn by plate is
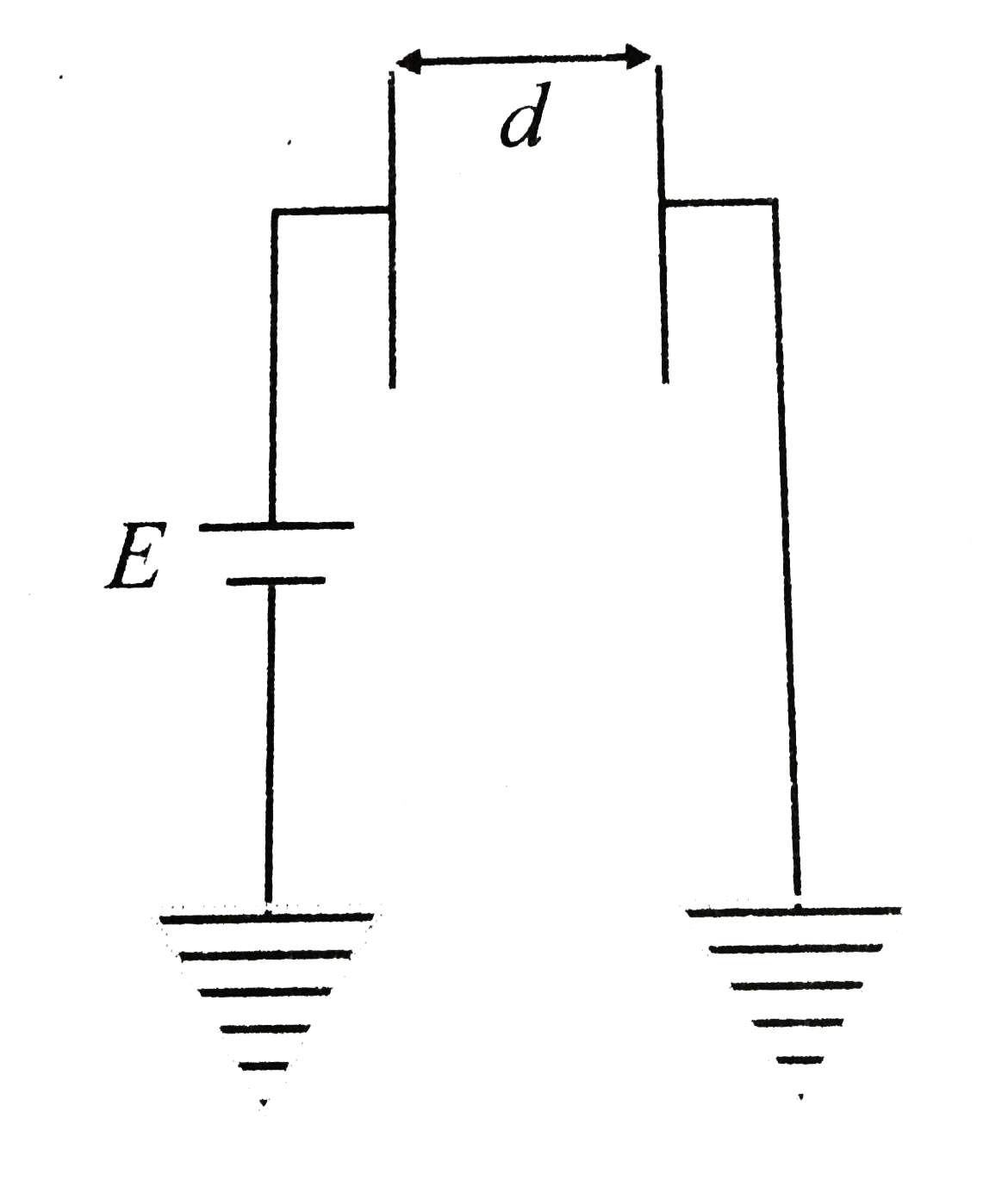 A2ε0AEdBε0AEdCε0AE2dD3ε0AEd
A2ε0AEdBε0AEdCε0AE2dD3ε0AEd
Two conducting plates A and B are placed parallel to each other. A is given a charge. Q1 and B a charge Q2. Find the distribution of charges on the four surface.
View SolutionTwo large conducting plates, identical in size, are placed parallel to each other at a separation d. Each plate has area A. One of the plates is cut into two equal parts and then a battery of emf V is connected across these two pieces. Find the work done by the battery in supplying charge to the plates.
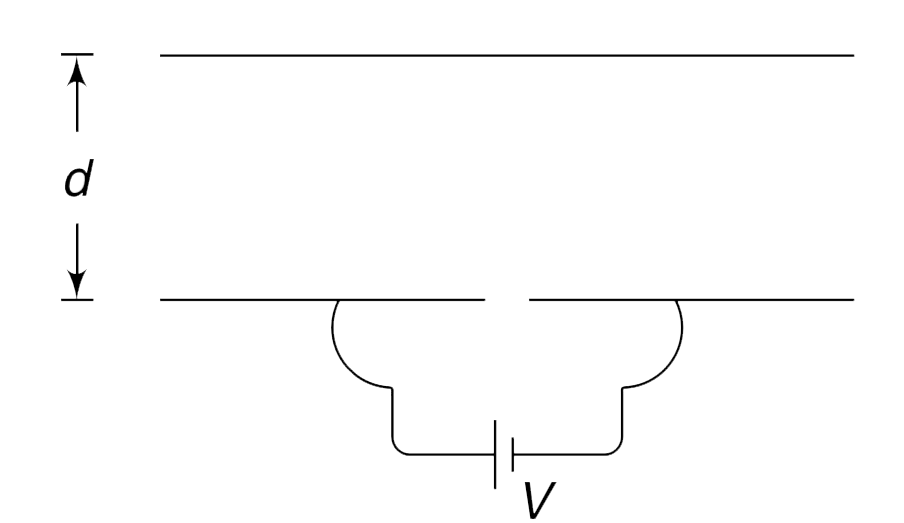 View Solution
View SolutionThree large plates A, B and C are placed parallel to each other and charges are given as shown. The charge that appears on the left surface of plate B is
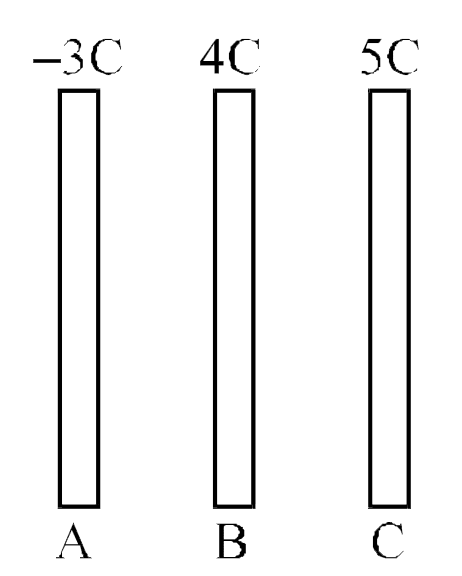 View Solution
View SolutionTwo large conducting plates are placed parallel to each other nad they carry equal and opposite charges with surface density σ as shown in figure (30-E6). Find the electric field (a) at the left of the plates, (b) in between the plates and © at the right of the plates.
 View Solution
View SolutionTwo conducting plates A and B are placed parallel to each other. A is given a charge Q1 and B a charge Q2. Prove that the charges on the inner surfaces are of equal magnitude and opposite sign.
View SolutionTwo large conducting plates X and Y. each having large surface area A (on one side), are placed parallel to each other as shown in figure (30-E7). The plate X ia given a charge Q whereas the other is neutral. Find (a) the surface charge dendity at the inner surface of the plates X, (b) the electric field at a point to the left of the plates, (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
 View Solution
View Solution

