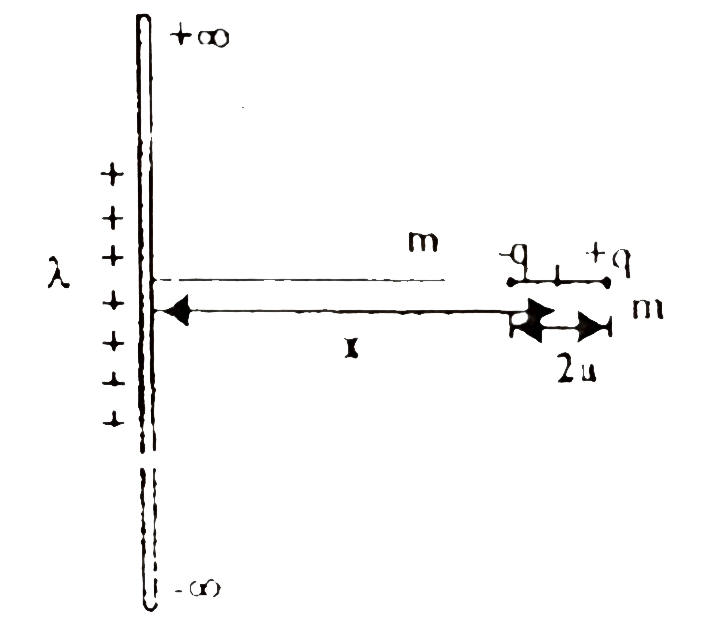
An electric dipole of dipole moment p is kept at a distance r form

A tiny electric dipole of dipole moment $p$ is palced at a distance $r$ from an infinitely long wire, with its $\to p$ normal to the wire. If the linear charge density of the wire is $λ$ , the electrostatic force acting on the dipole is equal to
A $\frac{λ P}{4 π ε_{0} r}$
B $\frac{λ P}{π ε_{0} r}$
C $\frac{2 λ P}{π ε_{0} r}$
D $\frac{λ P}{2 π ε_{0} r^{2}}$
A small electric dipole of dipole moment P is placed at a distance r from one infinitely long uniformly charged, straight conductor. If $λ$ is the linear charge density of straight conductor and axis of the dipole is perpendicular to the straight conductor then the force acting on the dipole is
A $\frac{λ P}{2 π ε_{0} r^{2}}$
B $\frac{λ P}{2 π ε_{0} r}$
C $\frac{λ P}{4 π ε_{0} r^{2}}$
D $\frac{λ P}{π ε_{0} r^{2}}$

An electric dipole of dipole moment p is kept at a distance r form infinite long charged wire of linear charge denisty $λ$ as shown . Find the force acting on the dipole ?