If the electric field is given by →E=(100x2)i the potential difference between points x=10m and x=20m in volts is
−5
5
−10
10
The correct Answer is:A
To find the potential difference between the points x=10m and x=20m given the electric field →E=100x2^i, we can follow these steps:
Step 1: Understand the relationship between electric field and potential
The electric field →E is related to the electric potential V by the equation:
→E=−∇V
In one dimension (along the x-axis), this simplifies to:
E=−dVdx
Step 2: Set up the integral for potential difference
The potential difference VAB between two points A and B can be calculated using the integral of the electric field:
VAB=VB−VA=−∫xBxAEdx
In our case, A is at x=10m and B is at x=20m.
Step 3: Substitute the electric field into the integral
Substituting E=100x2:
V20−V10=−∫2010100x2dx
Step 4: Calculate the integral
The integral can be computed as follows:
−∫2010100x2dx=−100(−1x)2010
Calculating the limits:
=−100(−120+110)
=−100(−120+220)=−100(120)
=−5volts
Step 5: Conclusion
The potential difference between the points x=10m and x=20m is:
V20−V10=−5volts
The electric field →E is related to the electric potential V by the equation:
→E=−∇V
In one dimension (along the x-axis), this simplifies to:
E=−dVdx
The potential difference VAB between two points A and B can be calculated using the integral of the electric field:
VAB=VB−VA=−∫xBxAEdx
In our case, A is at x=10m and B is at x=20m.
Substituting E=100x2:
V20−V10=−∫2010100x2dx
The integral can be computed as follows:
−∫2010100x2dx=−100(−1x)2010
Calculating the limits:
=−100(−120+110)
=−100(−120+220)=−100(120)
=−5volts
The potential difference between the points x=10m and x=20m is:
V20−V10=−5volts
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise-2(C.W)53videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE -2 (H.W)50videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise -1 (C.W)44videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -415videos
ELECTROMAGNETIC WAVES
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question11videos
ELECTROSTATICS AND GAUSS LAW
Similar Questions
Electric field in a region is given by E=(2ˆi+3ˆj−4ˆk)V/m. Find the potential difference between points (0, 0, 0) and (1,2,3) in this region.
View SolutionFigure shows the variation of electric field intensity E versus distance x. The magnitude potential difference between the point at x = 0 to x = 6 m will be
View Solution
Knowledge Check
- Question 1 - Select One
Find the potential difference between X and Y in volt is:-
 A1B−1C2D−2
A1B−1C2D−2 - Question 2 - Select One
Electric field at a distance x from the origin is given as E=100N−m2/Cx2 . Then potential difference between the points situated at x = 10 m and x = 20m is :-
A5 VB10 VC15 VD4V - Question 3 - Select One
Figure shows the variation of electric field intensity E with distance x. The potential difference between the point x = 0 and x= 5m is
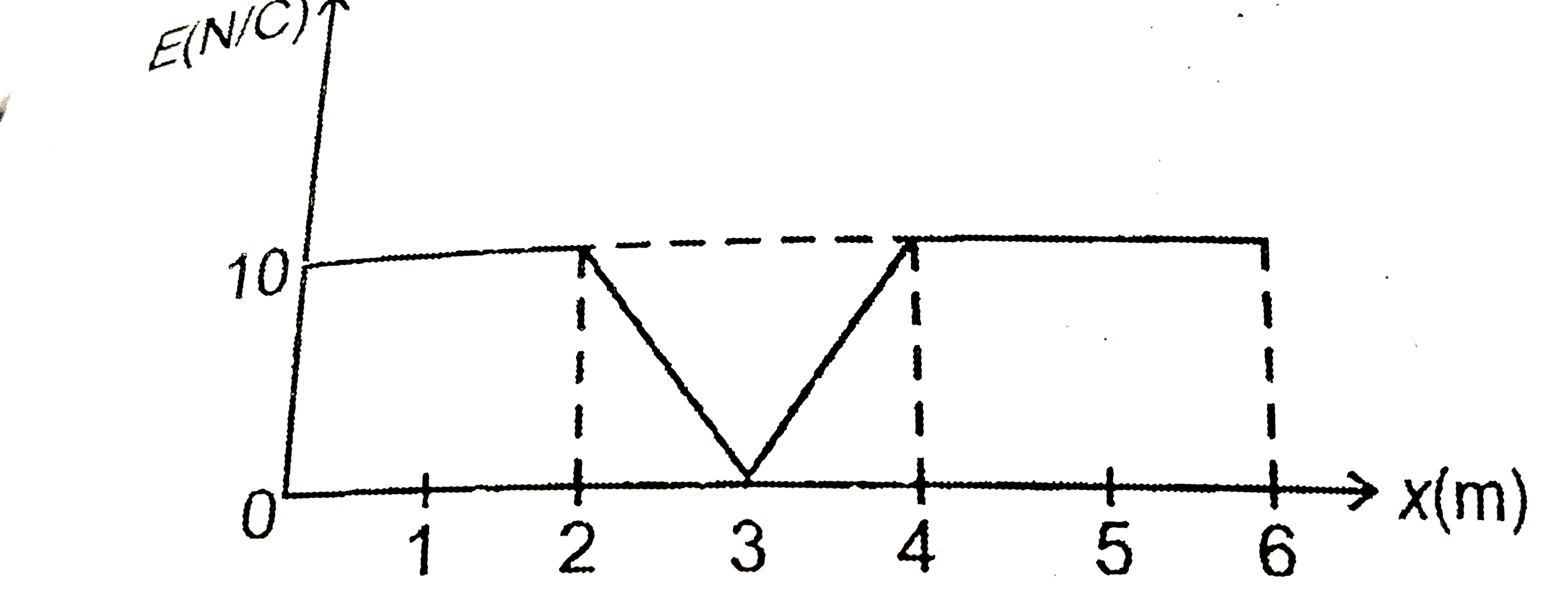 A40VB50VC30VD20V
A40VB50VC30VD20V
Electric field intensity in a region of space is given by →E=10x2ˆiN/C. What will be potential difference between point A(2, 5) and B(-1, 10)?
View SolutionMagnitude of electric field only on the x-coordinate as →E=20x2ˆiV/m. Find
(i) The potential difference between two points A (5m, 0) and B (10m, 0).
(ii) Potential at x=5 if V at ∞ is 10 volt.
(iii) In part (i), does the potential difference between a and B depend on whether the potential at ∞ is 10 volt or something else.View SolutionAn electric field is described as →E=ˆix+ˆkz.
The potential difference VAB (in volt) between A(0,0,0) and B(2,2,0) is :View SolutionFigure shows the variation of electric field intensity E versus distance x. What is the potential difference between the point at x = 2 m and at x = 6 m from O?
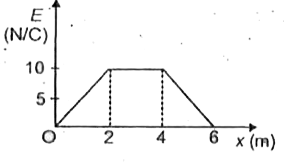 View Solution
View SolutionThe electric field in a certain region is given by →E=(Kx3)→i. The dimensions of K are -
View Solution

