The self inductance of the motor of an electric fan is 10H, in order to impart maximum power at 10Hz, it should be connected to a capacitance of
To solve the problem, we need to find the capacitance that should be connected to the motor of an electric fan to impart maximum power at a frequency of 10 Hz, given that the self-inductance (L) of the motor is 10 H.
1. Identify the Given Values:
- Self-inductance, L=10H
- Frequency, f=10Hz
2. Calculate Angular Frequency (ω):
ω=2πf
Substituting the value of f:
ω=2π×10=20πrad/s
3. Set Up the Condition for Maximum Power:
For maximum power transfer in an AC circuit, the inductive reactance (XL) must equal the capacitive reactance (XC):
XL=XC
Where:
XL=ωLandXC=1ωC
4. Equate Inductive and Capacitive Reactance:
ωL=1ωC
5. Rearranging to Find Capacitance (C):
C=1ω2L
6. Substituting the Values:
First, calculate ω2:
ω2=(20π)2=400π2
Using π2≈10:
ω2≈400×10=4000
Now substitute ω2 and L into the capacitance formula:
C=14000×10=140000F
7. Convert to Microfarads:
C=140000=25×10−6F=25μF
Final Answer:
The capacitance that should be connected to the motor of the electric fan to impart maximum power at 10 Hz is 25 microfarads.
---
- Self-inductance, L=10H
- Frequency, f=10Hz
ω=2πf
Substituting the value of f:
ω=2π×10=20πrad/s
For maximum power transfer in an AC circuit, the inductive reactance (XL) must equal the capacitive reactance (XC):
XL=XC
Where:
XL=ωLandXC=1ωC
ωL=1ωC
C=1ω2L
First, calculate ω2:
ω2=(20π)2=400π2
Using π2≈10:
ω2≈400×10=4000
Now substitute ω2 and L into the capacitance formula:
C=14000×10=140000F
C=140000=25×10−6F=25μF
The capacitance that should be connected to the motor of the electric fan to impart maximum power at 10 Hz is 25 microfarads.
Similar Questions
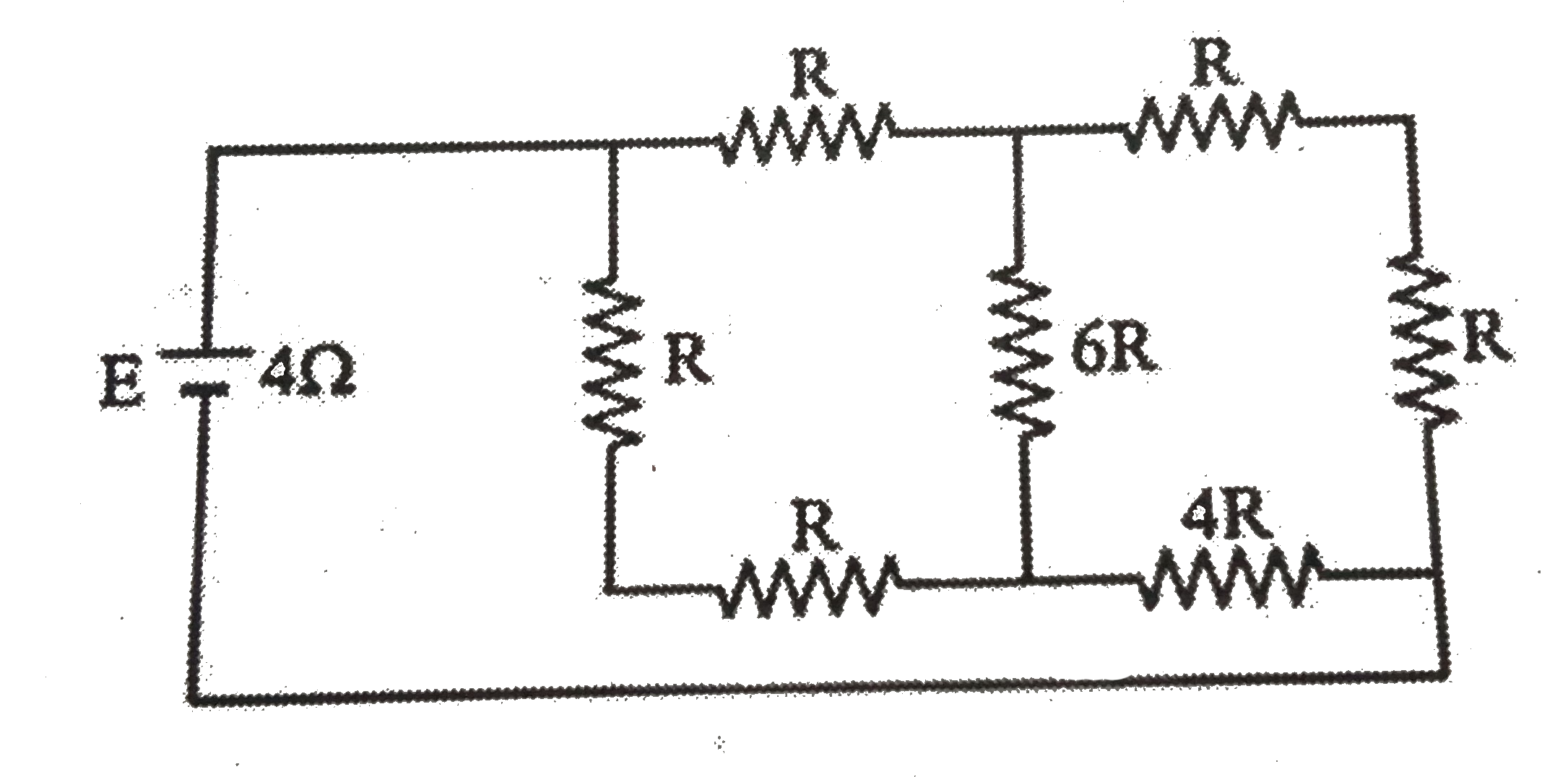
A battery of internal resistance 4Ω is connected to the network of resistance as shown. In order to give the maximum power to the network, the value of R should be-
View SolutionThe self inductance of a choke coil is 10mH. When it is connected to a 10VDC source, the loss of power is 20W. When it is connected to a 10V(AC) source, the loss of power is 10W. The frequency of (AC) source (in Hz ) will be (Answer to be given in nearest integer)
View Solution
Knowledge Check
The self inductance of the motor of an electric fan is 10H. In order to impart maximum power at 50 Hz, it should be connected to a capacitance of
A8μFB4mu FC2μFD1μFThe self inductance of the motor of an electric fan is 10 H. In order to impart maximum power at 50 Hz, it should be connected to a capacitance of:
A1μFB2μFC4μFD8μFThe self inductance of the motor of an electric fan is 10 H. In order to impart maximum power at 50 Hz, it should be connected to a capacitance of:
A4μFB8μFC1μFD2μF
Explain the phenomenon of self induction and mutual induction. Define coefficient of self induction and mutual induction. Write the SI unit and dimensions of coefficient of self induction.
A potentiometer wire has a length of 4m and a resistance of 5Ω. What resistance should be connected in series with a potentiomete-wire and a cell of e.m.f. 2V having internal resistance 1Ω to get a potential gradient of 10−3V/cm ?
View SolutionThe inductance of the motor of a fan is 1.0 H. To run the fan at 50 Hz the capacitance of the capacitor that will cancel its inductive reactance, will be -
View SolutionA battery of internal resistance 4Ω is connected to the network of resistance as shown. In order to give the maximum power to the network, the value of R should be-

View SolutionA battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
 .
.
View SolutionA battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
 .
.
View Solution
