The inductance of the motor of a fan is 1.0 H. To run the fan at 50 Hz the capacitance of the capacitor that will cancel its inductive reactance, will be -
10μ F
40μ F
0.4μ F
0.04μ F
The correct Answer is:A
To find the capacitance that will cancel the inductive reactance of a fan motor with an inductance of 1.0 H at a frequency of 50 Hz, we can follow these steps:
1. Understand the relationship between inductive reactance (XL) and capacitive reactance (XC):
- The inductive reactance XL is given by the formula:
XL=ωL
- The capacitive reactance XC is given by the formula:
XC=1ωC
- To cancel the inductive reactance, we set XL=XC.
2. Express angular frequency (ω) in terms of frequency (f):
- The angular frequency ω is related to the frequency f by:
ω=2πf
3. Substitute ω into the reactance equations:
- Substitute ω into the equation for XL:
XL=(2πf)L
- Substitute ω into the equation for XC:
XC=1(2πf)C
4. Set the two reactances equal to each other:
- From XL=XC:
(2πf)L=1(2πf)C
5. Rearrange the equation to solve for capacitance (C):
- Multiply both sides by C and rearrange:
C=1(2πf)2L
6. Substitute the known values:
- Given L=1.0H and f=50Hz:
C=1(2π⋅50)2⋅1
7. Calculate the value:
- First, calculate 2π⋅50:
2π⋅50≈314.16
- Now square this value:
(314.16)2≈98706.5
- Finally, calculate C:
C≈198706.5≈1.014×10−5F
8. Convert to microfarads:
- Since 1F=106μF:
C≈10.14μF
Final Answer:
The capacitance required to cancel the inductive reactance is approximately 10 microfarads.
---
- The inductive reactance XL is given by the formula:
XL=ωL
- The capacitive reactance XC is given by the formula:
XC=1ωC
- To cancel the inductive reactance, we set XL=XC.
- The angular frequency ω is related to the frequency f by:
ω=2πf
- Substitute ω into the equation for XL:
XL=(2πf)L
- Substitute ω into the equation for XC:
XC=1(2πf)C
- From XL=XC:
(2πf)L=1(2πf)C
- Multiply both sides by C and rearrange:
C=1(2πf)2L
- Given L=1.0H and f=50Hz:
C=1(2π⋅50)2⋅1
- First, calculate 2π⋅50:
2π⋅50≈314.16
- Now square this value:
(314.16)2≈98706.5
- Finally, calculate C:
C≈198706.5≈1.014×10−5F
- Since 1F=106μF:
C≈10.14μF
The capacitance required to cancel the inductive reactance is approximately 10 microfarads.
Similar Questions
Knowledge Check
The reactance of capacitor at 50Hz is 10Ω. What will be its reactance at 200Hz?
A10ΩB40ΩC2.5ΩD20ΩThe self inductance of the motor of an electric fan is 10 H. In order to impart maximum power at 50 Hz, it should be connected to a capacitance of:
A1μFB2μFC4μFD8μFThe self inductance of the motor of an electric fan is 10H. In order to impart maximum power at 50 Hz, it should be connected to a capacitance of
A8μFB4mu FC2μFD1μF
The self inductance of the motor of an electric fan is 10H, in order to impart maximum power at 10Hz, it should be connected to a capacitance of
View SolutionThe figure shows the graphical variation of the rectance of a capacitor with frequency of acsource.
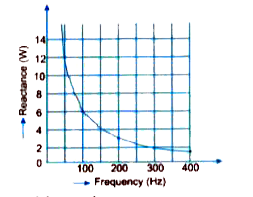
(a) Find the capacitance of the capacitor.
(b) An ideal inductor has the same reactance at 100 Hz frequency as the capacitor has at the same frequency. Find the value of inductance of the inductor.
(c ) Draw the graph showing the variation of the rectance of this inductor with frequency.
View Solution(a) What is the reactance of a 2.00H inductor at a frequency of 50.0Hz?
(b) What is the inductance of an inductor whose reactance is 2.00Ω at 50.0Hz?
(c) What is the reactance of a 2.00μF capacitor at a frequency of 50.0Hz?
(d) What is the capacitance of a capacitor whose reactance is 2.00Ω at 50.0Hz?
View SolutionThe self inductance of the motor of an electric fan is 10 H. In order to impart maximum power at 50 Hz, it should be connected to a capacitance of:
View SolutionReactance of a capacitor of capacitance 1/π farad at 50 Hz is
View Solution