A rectangular block of glass is placed on a printed page lying on a horizontal surface. Find the minimum value of the refractive index of glass for which the letters on the page are not visible from any of the vertical faces of the block.

The situation is as shown in the Fig, Light will not emerge our from the vertical face BD if
at it I >θcor sini >sinθc, sin I >1μ …........(1)
But from Snell’s law at O.
1×sinθ=μ sinr and ΔOPR ,
r+1=90∘,r=90∘ - i So sinθ=μsin(90∘−i)
cosi =(sinθμ)
But sini = √1−cos2i=√1−(sinθμ)2 .......(2)
Substituting the value of sin i from eq (2) in (1)
√1−sin2yheyaμ2>1μ,μ2>1+sin2θ
Now as (sin2θ)max=1,μ2>2,μ>√2
Hence μmin=√2
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFLECTION)
9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFRECTION)
28 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
A rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
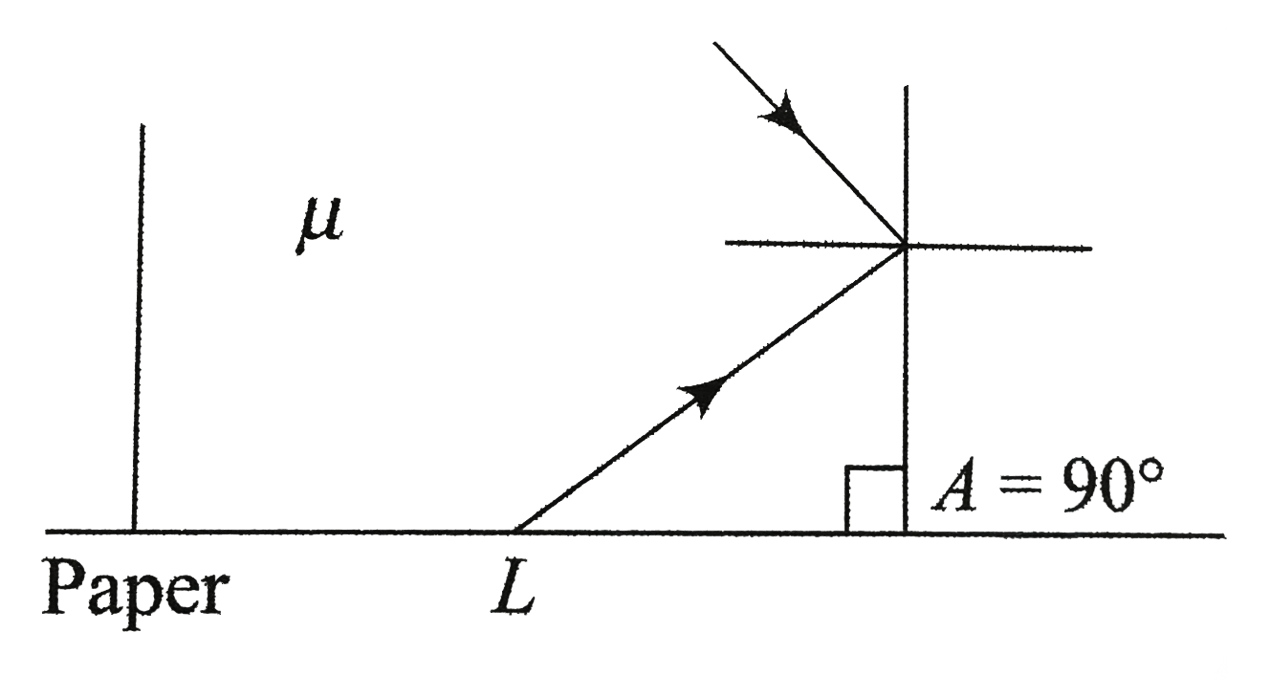
View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.

View Solution
Knowledge Check
Word ‘Newton’s printed on a paper and is placed on a horizontal surface below a cubical glass. The minimum value of refractive index of a cubical glass for which letters are not visible from any vertical faces, of the glass, is (Critical angle =45°)
A√3B0.5C1D√2A cubical transparent slab is used as a paper weight. What should be the minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces.
A√2B√3C√5D√5/√3A rectangular block of glass ABCD has a refractive index 1.6. A pin is placed midway on the faceAB, Fig. When observed from the face AD, the pin shall.
 .Aappear to be near A.Bappear to be near DCappear to be at the centre of ADDnot bee seen at all.
.Aappear to be near A.Bappear to be near DCappear to be at the centre of ADDnot bee seen at all.
A cubical transparent slab is used as a paper weight. What should be the minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces.
View SolutionA large rectangular glass block of refractive index μ is lying on a horizontal surface as shown in Figure. Find the minimum value of μ so that the spot S on the surface cannot be seen through top plane ‘ABCD’ of the block.
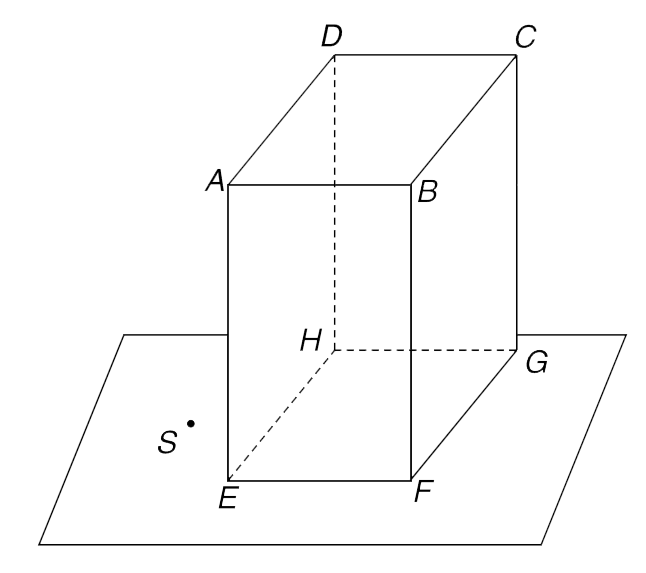
View SolutionA rectangular block of glass is placed on a mark made on the surface of the table and it is viewed from the vertical position of eye. If refractive index of glass be μ and its thickness d, then the mark will appear to be raised up by
View SolutionA ray of light normally on one of the faces of a right-angled isosceles glass prism is found to be totally reflected. What is the minimum value of the refractive index of the material of the prism ?
View SolutionA rectangular block of glass ABCD has a refractive index 1.6. A pin is placed midway on the face AB, Fig. When observed from the face AD, the pin shall.
 .
.
View Solution
